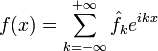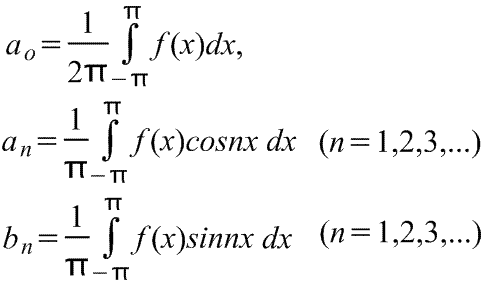Законы распределения непрерывных случайных величин

Билет №3

1. Извлечение корня из комплексного числа

5 ª√Z=ª√r(cos φ+2πk/а +i *sin φ+2πk/a) k∈(1;2;3…a-1)

Все корни А-ой степени лежат на окружности r=| Z |¹\а и являются вершинами правильного А-угольника, вписанного в эту окружность.

2. Закон распределения дискретной случайной величины

Законом распределения дискретной случайной величины называется соответствие между отдельными возможными значениями и их вероятностями .

Закон распределения дискретной случайной величины проще представить в виде таблицы распределения, в первой строке которой указывают возможные значения случайной величины, а во второй строке — соответствующие вероятности этих значений.

X	X1	X2	X3	…	xn
p	P1	P2	P3	…	pn

Здесь х1, х2, x3, х4,...,хn — значения, которые может принять случайная дискретная величина X и соответствующие вероятности

p1=Р(Х=х1), p2=Р(Х=х2),

p3=Р(Х=х3), p4=Р(Х=х4).

pn=Р(Х = хn) и p1+p2+p3+p4+...+pn=1

Билет №1

1. Комплексные числа и их изображение на плоскости. Аргумент, модуль комплексного числа. Алгебраическая, тригонометрическая и показательная форма комплексного числа

Опр. Комплексными числаминаз-ся пары действительных чисел (x,y) для которых определено понятие равенства и операции сложения и умножения следующим образом:

1. (x₁, y₁) = (x₂, y₂) ó x₁=x₂, y₁=y₂

2. (x₁, y₁) + (x₂, y₂) = (x₁+x₂, y₁+ y₂)

3. (x₁, y₁)(x₂, y₂)=(x₁x₂ - y₁ y₂ , y₁x₂ + x₁y₂)

Опр.Комплексное число(0,1) наз-сямнимой единицей и обозначается i; i²=(0,1)*(0,1)= -1

Опр.Частным комплекных чиселz₁ и z₂наз=-ся комплексное число z удовлетворяющее уравнению zz₂=z₁ =>

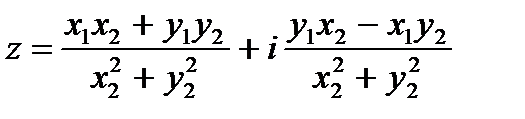
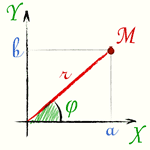
Опр. Аргументом компл. числаzназ-ся угол между вектором z и действительной осью. Угол отсчитывается от положительного направления оси, если отсчет идет против часовой стрелки, то угол считается положительным, если по часовой стрелке, - отрицательным.

Длина вектора, изображающего комплексное число, называется модулем комплексного числа. Модуль любого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + b·i обозначается |a + b·i|, а также буквой r. Из чертежа видно, что: r= | a+b·i |= Корень(a2+b2)

Комплексные числа, Алгебраическая, тригонометрическая и показательная формы. Геометрическая интерпретация. Формулы Эйлера.

Алгебраическая форма: множество пар (х,у)ЭR для которых определены следующие операции:

(х1, у1)= (х2, у2)x1=x2,y1=y2

(х1, у1)+(х2, у2)=(x1+x2,y1+y2)

(х1, у1)*(х2, у2)=(x1x2-y1y2,x1y2+x2y1)

Свойства:

z1+z2=z2+z1

(z1+z2)+z3=z1+(z2+z3)

Z+(0,0)=z

Z+(-z)=(0,0)

Z*(1,0)=1

(Z1+z2)z3=z1z3+z2z3

(z1z2)z3=z1(z2z3)

Z=x+iy – алгебраическая форма записи, где i – мнимая единица – корень изминус одного. Любое комплексное число при возведении в квадрат даст нам естественное число.

Угол между ох и радиус вектором обозначающим комплексное число называют аргументом комплексного числа и обозначают буквой фи. Z= r(cosφ+isinφ)

Свойства

z1z2=r1r2(cos (φ1+φ2)+i sin (φ1+φ2))

z1/z2=(r1/r2)( cos (φ1-φ2)+isin (φ1-φ2))

= (cos (n*φ)+i sin (n*φ))

=(cos ()+i sin ()) k?[1,n]?Z

Показательнаяформа: z=r. = cosφ+isinφ – формулаэйлера

Билет №5

1) ОПРЕДЕЛЕНИЕ. Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант х_i и соответствующих им частот n_i или относительных частот w_i

_{2) Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два возможных исхода и вероятности исходов остаются неизменными для всех испытаний.}

_{Обозначим эти вероятности как p и q. Исход с вероятностью p будем называть “успехом”, а исход с вероятностью q– “неудачей”.}

_{Очевидно, что}

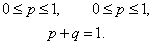
Формула Бернулли:

Билет №8

8.1..Мат. ожид. Св и его св-ва

Дискретная случайная величина Х задана рядом распределения х х1 х2 … хn р р1 р2 … рn Мат ожидание М(х) СВ Х дискретного типа наз. Сумма произведений случ. величин.М(х)=Х1Р1+Х2Р2+…+ХnPn , х<М(х) ≤xn Мат. ожид. это характеристика положения случ. величины.

Св-ва мат. ожид.:1)C=const M(c)=C 2) M(cx)=C•M(X),где С=const 3)мат.ожид су3ммы двух случ. величин равно сумме их мат.ожид. М(х+у)=М(х)+М(у)и М(х-у)=М(х)-М(у)4)Две случ.велич. Х и У наз. независимыми, если закон распредел одной из них не зависит от того, какое значение принимает другая величина. Несколько СВназ взаимно-независимыми, если закон распредел. любой из них не зависит от того , какие возможные значения приняли некоторые велич из оставшихся. М(ХУ)=М(Х)М(У), если Х,У независимые . М(Х1Х2…Хn)= М(Х1 )М(Х2 )…М(Хn)

8.2. Теорема сложения вероятностей несовместных событий.

Теор. Пусть А и В несовместные события. Тогда вероятность суммы этих событий=сумме их вероятностей. Р(А+В)=Р(А)+Р(В) (1).

Д-во: Пусть число всех исходов опытов n, пусть событию А благоприятствуют m1, из них В-m2 из них.

P(A)=m1/n P(B)=m2/n A+B=m1+m2 P(A+B)=(m1+m2)/n=m1/n+m2/n=P(A)+P(B) чтд

Билет № 7

1. Тригонометрический ряд Фурье — представление произвольной функции 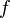с периодом в виде ряда

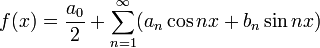или используя комплексную запись, в виде ряда:

7.2.Формула полной вероятности.

Предположим, что событие А происходит одновременно с одним из событий H1, H2,…,Hn, попарно несовместных и образующих полную группу событий.Т.к. заранее неизвестно, с каким из событий Hi событие А произойдет, то H1…Hn – гипотезы. Вероятность P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+…+P(Hn)P(A/Hn).ИлиP(A)=

Доказательство:А=AH1+AH2+…+AHn. Т.к. события Hi попарны и несовместны, то будут попарными и несовместными и события AHi. По теореме несовместных событий получаем P(A)=P(AH1+AH2+ …+AHn)= P(H1)+…+P(Hn). P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+…+P(Hn)P(A/Hn).

Замечание1: Т.к. H1,…,Hn образуют полную вероятность, то сумма вероятностей равна 1: P(H1)+ P(H2)+…+ P(Hn)=1.

Замечание2: Вероятности гипотез определяются до опыта и называются априорными

Билет № 13

2.Теорема. Вероятность суммы 2-х несовместных событий равна сумме вероятностей этих событийp(A+B)=p(A)+p(B)

Билет №18

1.Отклонение случайной величины от ее математического ожидания Каждое из слагаемых правой части равенства есть математическое ожидание числа появлений события в одном испытании. Так как математическое ожидание числа появлений события в одном испытании равно вероятности события, то M[X1] = p, M[X2] = p, . . ., M[Xn] = p, или M[X] = np.

2. Невозможным называется событие, которое при проведении данного случайного эксперимента никогда не происходит. Например, события

Пример при подбрасывании игрального кубика выпадет 7 очков;

Достоверным называется событие, которое обязательно наступает при проведении данного случайного эксперимента. Например, события

Примерпри подбрасывании игрального кубика выпадет меньше 7 очков;

События А и В, связанные с некоторым опытом, называются совместными, если существует испытание, при котором реализуются оба события.

События А и В, связанные с некоторым опытом, называются несовместными, если не существует испытания, при котором реализуются оба события

События А, Б, В... называют зависимыми друг от друга, если вероятность появления хотя бы одного из них изменяется в зависимости от появления или непоявления других событий. Примером зависимых событий являются события, происходящие при отборе единиц из совокупности по схеме невозвращенного шара, когда от появления годного или бракованного изделия при первом испытании зависит вероятность появления годного изделия при втором испытании.
События называются независимыми, если вероятности появления каждого из них не зависят от появления или непоявления прочих из них.

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А — деталь годная, В — деталь окрашенная, то АВ — деталь годна и окрашена.

Билет №19

1. Среднее квадратичное отклонение определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из дисперсии и может быть найдена так:

1. Для первичного ряда:

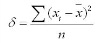
2. Для вариационного ряда:

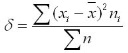
Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:

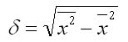
Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.

2. локальная Теорема Муавра — Лапласа —. Если при каждом из n независимых испытаний вероятность появления некоторого случайного события Е равна р (0<р<1) и m — число испытаний, в которых Е фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа.

Интегральная теорема Муавра – Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n независимых испытаниях собы­тие А состоится число раз, заключенное в границах от а до b включительно (а <b), приближенно равна: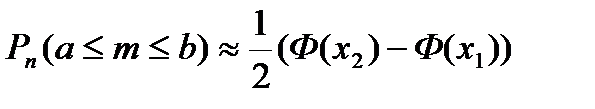

,

где функция Ф (х) определяется равенством

,

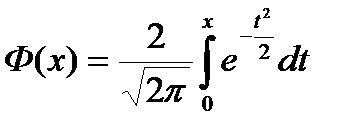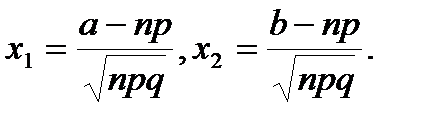
Билет №20

1. Если дана случайная величина определённая на некотором вероятностном пространстве, то:

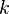- -м нача́льным моментом случайной величины 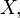где 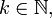называется величина

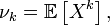
если математическое ожидание 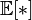в правой части этого равенства определено;

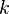- -м центра́льным моментом случайной величины 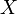называется величина

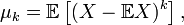
2.Биномиа́льноераспределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из 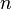независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна .

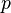Билет №22.

1. Оценка отклонения теоретического распределения от нормального; асимметрия и эксцесс. При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики (асимметрию и эксцесс). Для нормального распределения эти характеристики равны 0, поэтому, если для изучаемого теоретического распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот большие значения a_X и e_X, указывают значительные отклонения от нормального. Пологая часть правее моды, значит a_X>0 Пологая часть левее моды, значит a_X<0. Замечание.При исследовании эксцесса надо считать, что нормальное исследуемое распределение, имеют одинаковое МО и дисперсию.

2.Математическое ожидание случайной величины

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .

Математическое ожидание дискретной случайной величины x , имеющей распределение

называется величина 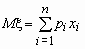, если число значений случайной величины конечно.

Если число значений случайной величины счетно, то 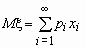. При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Математическое ожидание непрерывной случайной величины с плотностью вероятностей p_x(x) вычисляется по формуле 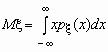. При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Если случайная величина h является функцией случайной величины x , h = f(x), то

.

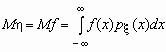Аналогичные формулы справедливы для функций дискретной случайной величины:

, .

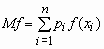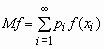Основные свойства математического ожидания:

-математическое ожидание константы равно этой константе, Mc=c ;

-математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и bсправедливо: M(ax + bh ) = a M(x )+ b M(h );

-математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).

Дисперсия случайной величины

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx =M(x - Mx )².

Легко показать, что Dx = M(x - Mx )²= Mx ² - M(x )².

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx ² >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

, .

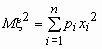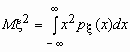Для определения меры разброса значений случайной величины часто используетсясреднеквадратичное отклонение 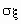,связанное с дисперсией соотношением .

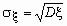Основные свойства дисперсии:

-дисперсия любой случайной величины неотрицательна, Dx 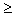0;

-дисперсия константы равна нулю, Dc=0;

-для произвольной константы D(cx ) = c²D(x );

-дисперсия суммы двух независимых случайных величинравна сумме их дисперсий: D(x ±h ) = D(x ) + D (h ).

Билет №23

Билет№ 16

Билет№2

1. Возведение в степень. Формула Муавра

При возведении комплексного числа в любую целую степень модуль комплексного числа возводится в ту же степень, а аргумент умножается на показатель степени.

Zª=rª(cosAφ+i*sin Aφ)

Данная формула называется формулой Муавра. Она верна и для целого отрицательного значения n, а также для n = 0.

2.Математическое ожидание случайной величины

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины  обозначается M .

Математическое ожидание дискретной случайной величины  , имеющей распределение

x1	x2	...	xn
p1	p2	...	pn

называется величина 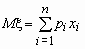, если число значений случайной величины конечно.

Если число значений случайной величины счетно, то 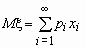. При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина  не имеет математического ожидания.

Математическое ожидание непрерывной случайной величины с плотностью вероятностей p_(x) вычисляется по формуле 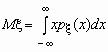. При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина  не имеет математического ожидания.

Если случайная величина  является функцией случайной величины  ,  = f(x), то

.

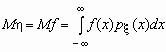Аналогичные формулы справедливы для функций дискретной случайной величины:

, .

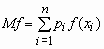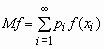Билет №10

Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.

В ранжированных рядах несгруппированные данные для нахождения медианы сводятся к поиску порядкового номера медианы. Медиана может быть вычислена по следующей формуле:

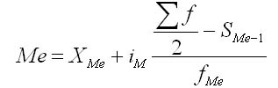
где Хm — нижняя граница медианного интервала;

im — медианный интервал;

Sme— сумма наблюдений, которая была накоплена до начала медианного интервала;

fme — число наблюдений в медианном интервале.

Билет №24

1.

Билет 21

1) Функция распределения плотности вероятностей и ее свойства.

Из формулы P{Α ≤ X < Β}=F(Β)-F(Α)следует, что вероятность попадания случайной величины в заданный интервал определяется скоростью изменения функции распределения вероятностей на этом интервале. Скорость изменения непрерывной функции равна ее производной. Это позволяет ввести новую функцию для задания случайной величины. Рассмотрим снова вероятность попадания случайной величины в интервал [x,x+Δx]:

P{x≤X<x+Δx}=F(x+Δx)-F(x).

Пусть Х - непрерывная случайная величина. Тогда для малых значений Δx эта вероятность будет также достаточно малой. Поделим ее на Δx и перейдем к пределу при Δx →0:

limΔx →0(P{x≤X<x+Δx}/Δx)=limΔx →0(F(x+Δx)-F(x))/Δx).

Если это предел существует, то он равен производной от функции распределения F(x):

limΔx →0(F(x+Δx)-F(x))/Δx)=F'(x)=f(x).

Функция f(x) называется плотностью распределения вероятностей случайной величины Х. Из определения следует, что при малых значениях Δx справедливо равенство:

P{x≤X<x+Δx}≈f(x)*Δx

2) Нормальное распределение,[1][2] также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности распределения:

где параметр μ — математическое ожидание, медиана и мода распределения, а параметр σ - стандартное отклонение(σ² — дисперсия) распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Многомерный случай описан в многомерном нормальном распределении.

Равномерное распределение.
Пусть сегмент [a,b] оси Ox есть шкала некоторого прибора. Допустим, что вероятность попадания указателя в некоторый отрезок шкалы пропорциональна длине этого отрезка и не зависит от места отрезка на шкале. Отметка указателя прибора есть случайная величина могущая принять любое значение из сегмента [a,b]. Поэтому . Если, далее, x1 иx2 (x1<x2) - две любые отметки на шкале, то согласно условию имеем

где k - коэффициент пропорциональности, не зависящий от x1 и x2, а разность x2-x1, - длина сегмента [x1,x2]. Так как при x1=a и x2=b имеем , то k(b-a)=1, откуда k=1/(b-

Билет 17

2) Полная группа событий.
Теорема. Сумма вероятностей событий А₁ , А₂ , ..., А_n , образующих полную группу, равна единице:

Р (A₁) + Р (А₂) + ... + Р (А_n) = 1.

Противоположные события.
Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через A, то другое принято обозначать

Билет 15

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны - это типичные практические примеры применения периодических функций в инженерных расчетах.

Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):

Стандартная (=обычная) запись через сумму sinx и cosx

f(x)=a_o+ a₁cosx+a₂cos2x+a₃cos3x+...+b₁sinx+b₂sin2x+b₃sin3x+...,

где a_o, a₁,a₂,...,b₁,b₂,.. - действительные константы, т.е.

Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:

Коэффициенты a_o,a_n и b_n называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a₁cosx+b₁sinx) называется первой или основной гармоникой,

Четные и нечетные функции.

Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х² и у=cosx.

Говорят, что функция y=f(x) нечетная,если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.

14.2. Геометрическая вероятность. Примеры.Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω: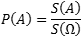

Пример 1. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга. Р е ш е н и е. Площадь кольца (фигуры g) S_g = p (10² — 5²) = 75p. Площадь большого круга (фигуры G)S_G = p10² = 100p.Искомая вероятностьР = 75p / (100p) = 0,75.

Пример 2. В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равновозможно в любой момент промежутка времени длительностью Т. Моменты поступления сигналов независимы один от другого.Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t (t < T). Найти вероятность того, что сигнализатор сработает за время T, если каждое из устройств пошлет по одному сигналу.Р е ш е н и е. Обозначим моменты поступления сигналов первого и второго устройств соответственно через х и у. В силу условия задачи должны выполняться двойные неравенства: 0 <= x <= Т, 0 <= y <= Т. Введем в рассмотрение прямоугольную систему координат хОу. В этой системе двойным неравенствам удовлетворяют координаты любой точки квадрата ОТ AT. Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют все возможные значения моментов поступления сигналов.Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t, т. е. если
у — х < t при у > х и х — у < t при х > у, или, что то же,y< x + t при у > х, (*)y > х - t при y < х. (**)Неравенство (*) выполняется для тех точек фигуры G, которые лежат выше прямой у = х и ниже прямой y = x + t, неравенство (**) имеет место для точек, расположенных ниже прямой у = х и выше прямой у = х - t.Все точки, координаты которых удовлетворяют неравенствам (*) и (**), принадлежат заштрихованному шестиугольнику. Таким образом, этот шестиугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими моментами времени х и у. Искомая вероятность Р = Пл.g / Пл.G = (Т² — (Т — t)²) / T² = (t (2T — t)) / T².

Билет №4

1) Функция комплексного переменного. Это понятие — обобщение предыдущего варианта: 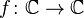.Такими функциями занимается отдельная область математического анализа — теория функций комплексного переменного, или комплексный анализ.Функция также может быть представлена в виде

,

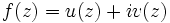однако имеется более глубокая связь между u и v. Например, для того, чтобы функция 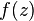была дифференцируема, должны выполняться условия Коши — Римана:

;

.

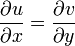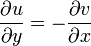Определение 1: Комплексным числом z называется пара действительных чисел (x,y), такая что z = x + i*y. x является действительной частью комплексного числа z и обозначается x = Re(z), а y - мнимая часть комплексного числа z и обозначается y = Im(z), i - мнимая единица : i*i = - 1, т.е. мнимая единица в квадрате равна минус единице.

Билет №6

1)Возведение в степень — бинарная операция, первоначально происходящая из многократного умножения натурального числа на самого себя. Обозначение: 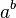называетсястепенью с основанием 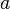и показателем .

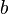Формула Муавра для комплексных чисел 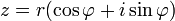утверждает, что

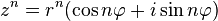
для любого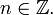

Формула названа по имени установившего её в 1707 году математика И. Муавра, друга великого И. Ньютона; современный вид формуле придал Л. Эйлер.

Доказательство [править]

Формула Муавра сразу следует из формулы Эйлера 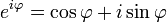и тождества для экспонент 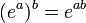, где b — целое число.^[1]

Применение [править]

Аналогичная формула применима также и при вычислении корней n-ой степени из ненулевого комплексного числа:

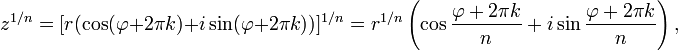
где k = 0, 1, …, n—1.

Вероятность гипотез

Вероятность гипотез.

Пусть событие А может наступить при условии появления одного из несовместных событий В1,В2,?Вn, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности:

Р(А) = Р(В1)?РВ1(А) + Р(В2) ?РВ2(А)+ ? +Р(Вn) ?РВn(А)

Формула Байеса:

,

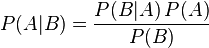где

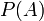— априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

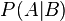— вероятность гипотезы A при наступлении события B (апостериорная вероятность);

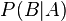— вероятность наступления события B при истинности гипотезы A;

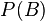— полная вероятность наступления события B.

Пример:

Пример расчёта

Пусть вероятность брака у первого рабочего 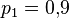, у второго рабочего — 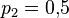, а у третьего — 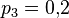. Первый изготовил 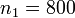деталей, второй — 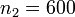деталей, а третий — 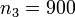деталей. Начальник цеха берёт случайную деталь, и она оказывается бракованной. Спрашивается, с какой вероятностью эту деталь изготовил третий рабочий?

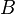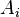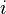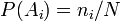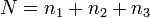Cобытие — брак детали, событие — деталь произвёл рабочий . Тогда , где , а 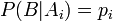. По формуле полной вероятности

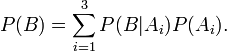
По формуле Байеса получим:

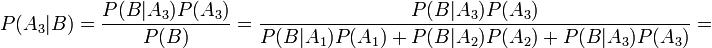
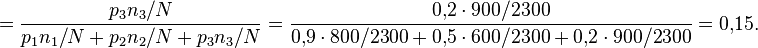
Билет №12

1. Тригонометрический ряд Фурье — представление произвольной функции с периодом 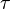в виде ряда

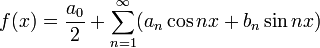или используя комплексную запись, в виде ряда:

коэффициентыao,an и bn называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье

Стандартная (=обычная) запись через сумму sinx и cosx

f(x)=ao+ a1cosx+a2cos2x+a3cos3x+...+b1sinx+b2sin2x+b3sin3x+...,

где ao, a1,a2,...,b1,b2,.. - действительные константы, т.е.

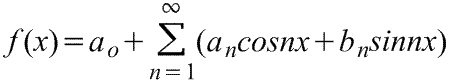
2.Противоположные события.
Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через A, то другое принято обозначать

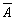
Теорема. Сумма вероятностей противоположных событий равна единице:

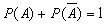
Примеры:

Пример 1. Попадание и промах при выстреле по цели — противоположные события. Если А — попадание, то противоположное событие — промах.

Пример 2. Из ящика наудачу взята деталь. События «появилась стандартная деталь» и «появилась нестандартная деталь» — противоположные

Вероятность противоположного события, очевидно, равна 10 / 21, что и утверждалось выше. [1]

Вычислим вероятность противоположного события А. Событие состоит в том, что выбранный номер не содержит ни одной из трех данных цифр. [2]

Сумма вероятностей противоположных событий равна единице. [3]

При этом вероятность противоположного события А будет больше, чем 1-а, то есть будет так же близка к единице, как вероятность события А близка к нулю

Билет №9

1. Полигоном частот называют ломанную, отрезки которой соединяют точки (x₁; n₁), (x₂; n₂), ..., (x_k; n_k). Для построения полигона частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им частоты n_i. Точки ( x_i; n_i) соединяют отрезками прямых и получают полигон частот

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению n_i / h (плотность частоты).

2. События А и В называются независимыми, если Р(АВ) = Р(А) Р(В). Несколько событий А, В, С,… называются независимыми, если вероятность их совместного осуществления равна произведению вероятностей осуществления каждого из них в отдельности: Р(АВС…) = Р(А)Р(В)Р(С)…

Иногда соотношение Р(АВ) = Р(А) Р(В|A) = P(B)P(A|B), справедливое при P(A)P(B) > 0,называют также теоремой умножения вероятностей

Билет №11

1) Случайную величину Х называют непрерывной (непрерывно распределенной) величиной, если существует такая неотрицательная функция p(t), определенная на всей числовой оси, что для всех х функция распределения случайной величины F(x) равна:

.

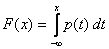
При этом функция p(t) называется плотностью распределения вероятностей непрерывной случайной величины.

Если такой функции p(t) не существует, то Х не является непрерывно распределенной случайной величиной.

Таким образом, зная плотность распределения, по формуле (6.7) можно легко найти функцию распределения F(x). И, наоборот, по известной функции распределения можно восстановить плотность распределения:

.

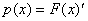
Свойства плотности распределения вероятностей

непрерывной случайной величины:

1. Плотность распределения – неотрицательная функция:

p(t)³0.

Геометрически это означает, что график плотности распределения расположен либо выше оси Ох, либо на этой оси.

2. 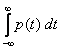=1.

Учитывая, что F(+¥)=1, получаем: 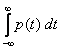=1. Т.е. площадь между графиком плотности распределения вероятностей и осью абсцисс равна единице.

Эти два свойства являются характеристическими для плотности распределения вероятностей. Доказывается и обратное утверждение:

2)

Суммой событий А и В называется третье событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.

Произведением событий А и В называется третье событие АВ, которое наступает тогда и только тогда, когда оба события: А и В.

Понятия суммы и произведения двух событий очевидным образом переносятся на случай любого множества событий.

Событием, противоположным событию А, называется событие , которое наступа