Связь понятий предел функции и предел последовательности
Между понятиями «предел функции» и «предел последовательности» существует связь, которая дается нижеследующей теоремой.
Теорема. Для того, чтобы существовал 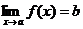 необходимо и достаточно, чтобы для любой последовательности
необходимо и достаточно, чтобы для любой последовательности 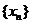 , у которой
, у которой  выполнялось условие
выполнялось условие 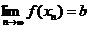 .
.
Доказательство.
Необходимость. Пусть 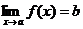 .Это значит, что
.Это значит, что
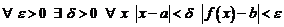 .
.
Возьмем любую последовательность 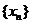 у которой
у которой  . Это значит, что
. Это значит, что
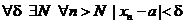 .
.
(Обратите внимание, какая буква написана после квантора " и где стоит эта же самая буква в предыдущей формуле!)
Совершим «прогулку» по этим выражениям по следующему маршруту:
"e > 0 ® $d >0 ® "d ® $N ® "n > N ® | xn -a |<d ® | x - a|<d ® | f(x) - b | < e.
Оставляя только подчеркнутые куски и заменяя в последних выражениях х на хn, получим
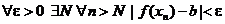 ,
,
что и говорит о том, что 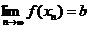 .
.
Достаточность. Докажем достаточность методом «от противного».
Прежде всего напомним, как пишется противоположное утверждение для строчки кванторов. Здесь действует следующее правило: чтобы написать противоположное утверждение, надо сделать следующее:
1. заменить квантор " на квантор $, и наоборот, квантор $ на квантор ";
2. последнее утверждение заменить на противоположное.
А теперь приступим к доказательству. Итак
Надо доказать:
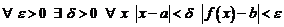 .
.
Противоположное утверждение имеет вид
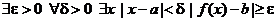 .
.
Сведем это утверждение к противоречию.
Берем то e > 0, которое «существует». Далее, возьмем последовательность 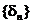 такую, что
такую, что
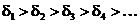 ,
, 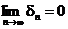 .
.
Тогда, согласно противоположному утверждению,
для d1 существует х1 такое, что 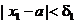 , но
, но 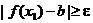 ;
;
для d2 существует х2 такое, что 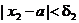 , но
, но 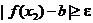 ;
;
для d3 существует х3 такое, что 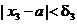 , но
, но 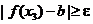 ;
;
и вообще
для dn существует хn такое, что 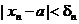 , но
, но 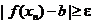 .
.
В результате получается некоторая последовательность 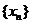 . Что хорошего можно о ней сказать?
. Что хорошего можно о ней сказать?
1. так как, по построению "n 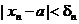 и
и 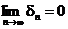 , то
, то 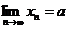 ;
;
2. но "n 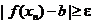 . Поэтому
. Поэтому 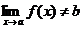 ! (Заметим, что этот предел может и вообще не существовать).
! (Заметим, что этот предел может и вообще не существовать).
Но это противоречит условию «для любой последовательности», которое стоит в формулировке теоремы. Это и доказывает достаточность. <
2.13 Свойства предела функции
Предельное значение функции обладает теми же свойствами, что и пределы последовательности, в частности
1. 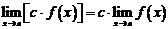
2. 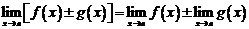
3. 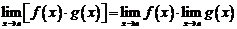
4. 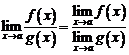 если
если 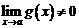
5. Если 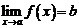 и
и 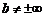 , то в некоторой окрестности
, то в некоторой окрестности 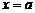
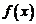 ограничена
ограничена
6. Если 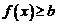 то
то 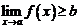 .
.
Докажем, например, свойство 3. Берем любую последовательность 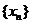 у которой
у которой .Для нее верно соотношение
.Для нее верно соотношение
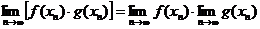 .
.
Но так как это верно для любой последовательности с указанным свойством, то, по только что доказанной теореме, верно и свойство
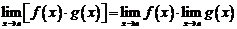 .
.
Остальные свойства доказываются аналогично.
2.14 Предел монотонной функции
Определение. Функция 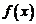 называется
называется
- монотонно возрастающей, если из 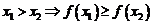
- строго монотонно возрастающей, если из 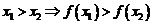
- монотонно убывающей, если из 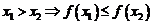
- строго монотонно убывающей, если из 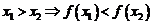 .
.
Докажем одну из возможных здесь теорем.
Теорема. Если 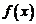 монотонно возрастает и ограничена сверху при
монотонно возрастает и ограничена сверху при 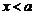 , то существует конечный предел слева
, то существует конечный предел слева 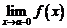 .
.
Доказательство.
Рассмотрим множество 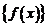 значений функции
значений функции 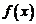 при
при 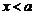 . По условию теоремы, это множество ограниченно сверху, то есть
. По условию теоремы, это множество ограниченно сверху, то есть 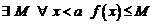 . По теореме о существовании супремума отсюда следует, что существует конечный
. По теореме о существовании супремума отсюда следует, что существует конечный 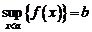 .
.
Покажем, что 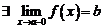 . По свойствам супремума
. По свойствам супремума
1. 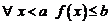 ;
;
2. 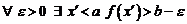 .
.
 |
Обозначим 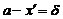 . Возьмем любое
. Возьмем любое 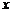 , для которого
, для которого 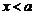 , но
, но 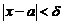 . Как видно из рисунка, из этого следует, что
. Как видно из рисунка, из этого следует, что 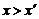 . Но тогда, в силу монотонности
. Но тогда, в силу монотонности 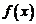 ,
,
а) 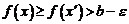 ,
,
б) 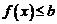 .
.
Поэтому имеем
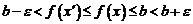
Выбрасывая лишнее, получим, что
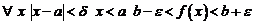
или, что то же самое, 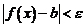 . По определению предела функции это означает, что
. По определению предела функции это означает, что 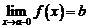 . <
. <
Аналогичные теоремы можно сформулировать и доказать также для монотонно убывающих функций, а так же для пределов слева.
2.15 Признак Больцано-Коши для функции
Теорема. Для того, чтобы существовал конечный предел 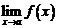 необходимо и достаточно чтобы
необходимо и достаточно чтобы
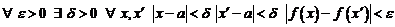 .
.
Доказательство.
Необходимость. Пусть существует конечный предел 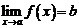 . Это значит, что
. Это значит, что
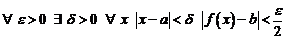 .
.
Но тогда 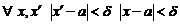 имеем
имеем
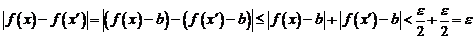
что и сказано в условии теоремы.
Достаточность. Достаточность будем доказывать сводя этот признак к случаю признака Больцано-Коши для последовательности.
1. Сведение к пределу последовательности
Итак, пусть
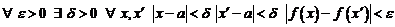
Возьмем любую последовательность  , сходящуюся к а, то есть у которой
, сходящуюся к а, то есть у которой 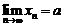 . Это значит, что
. Это значит, что
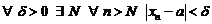 .
.
Но тогда 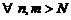 будут выполнены условия
будут выполнены условия 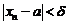 ,
, 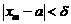 и получится, что
и получится, что 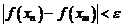 . Итак, получилось, что
. Итак, получилось, что
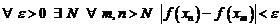 .
.
По признаку Больцано-Коши для последовательности, отсюда следует, что существует конечный 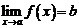 .
.
2. Независимость от выбора последовательности.
Возникающая здесь трудность заключается в том, что значение предела b может зависеть от выбора последовательности  . Покажем, что этого не может быть.
. Покажем, что этого не может быть.
Пусть имеется последовательность 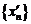 для которой также верно, что
для которой также верно, что 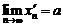 , но
, но 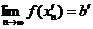 .
.
Составим «cмешанную» последовательность вида
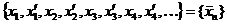 .
.
Так как и 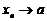 и
и 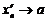 то ясно, что
то ясно, что 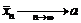 . Тогда теми же рассуждениями, что и в п. 1 показывается, что существует
. Тогда теми же рассуждениями, что и в п. 1 показывается, что существует 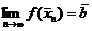 .
.
Но и 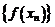 и
и 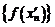 есть подпоследовательности последовательности
есть подпоследовательности последовательности 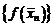 , а как показано выше, любая подпоследовательность сходится к тому же пределу, что и исходная последовательность. Поэтому
, а как показано выше, любая подпоследовательность сходится к тому же пределу, что и исходная последовательность. Поэтому
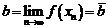
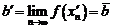
отсюда и следует, что 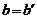 .
.
Независимость 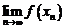 от вида последовательности
от вида последовательности  и говорит о том, что
и говорит о том, что 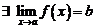 . <
. <
2.16 Сравнение бесконечно малых и бесконечно больших величин.
Определение. Функция 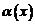 называется бесконечно малой величиной при
называется бесконечно малой величиной при 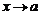 если
если 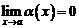 .
.
Пусть имеются две бесконечно малые величины 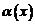 и
и 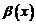 . Тогда возможны следующие варианты:
. Тогда возможны следующие варианты:
1. Существует 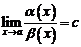 и
и 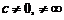 .
.
В этом случае говорят, что бесконечно малые величины 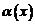 и
и 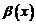 имеют одинаковый порядок малости и обозначают это так:
имеют одинаковый порядок малости и обозначают это так: 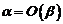 или, что то же самое,
или, что то же самое, 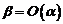 (символ
(символ 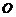 читается «О большое»)
читается «О большое»)
2. 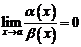 или, что то же самое,
или, что то же самое, 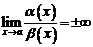 .
.
В этом случае говорят, что 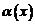 имеет более высокий порядок малости, чем
имеет более высокий порядок малости, чем 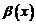 и обозначают это так:
и обозначают это так: 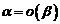 (символ «
(символ « 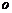 » читается «о малое»)
» читается «о малое»)
3. 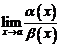 не существует.
не существует.
В этом случае говорят, что бесконечно малые 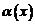 и
и 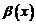 несравнимы.
несравнимы.
Для стандартизации вводят стандартную бесконечно малую величину 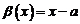 . Пусть при некотором
. Пусть при некотором 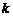 существует
существует 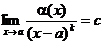 и
и 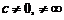 . В этом случае говорят, что
. В этом случае говорят, что 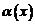 является бесконечно - малой
является бесконечно - малой 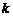 -го порядка и записывают это так
-го порядка и записывают это так
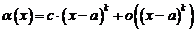 .
.
Выражение 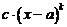 называют главным членом
называют главным членом 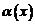 .
.
Определение. Функция 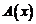 называется бесконечно большой при
называется бесконечно большой при 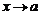 если
если 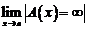 .
.
Пусть 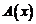 и
и 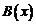 две бесконечно большие величины. Тогда возможны следующие варианты.
две бесконечно большие величины. Тогда возможны следующие варианты.
1. Существует 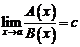 , и
, и 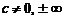 .
.
В этом случае говорят, что 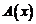 и
и 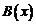 две бесконечно большие одного порядка.
две бесконечно большие одного порядка.
2. 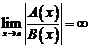 или, что то же самое,
или, что то же самое, 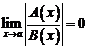 .
.
В этом случае говорят, что 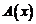 является бесконечно большой более высокого порядка, чем
является бесконечно большой более высокого порядка, чем 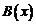 .
.
3. 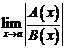 не существует.
не существует.
В этом случае говорят, что бесконечно большие 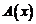 и
и 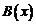 несравнимы.
несравнимы.
В качестве стандартной бесконечно большой величины берут 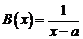 . Пусть при некотором
. Пусть при некотором 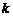 существует
существует 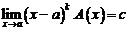 , и
, и 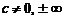 . В этом случае говорят, что
. В этом случае говорят, что 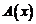 является бесконечно большой
является бесконечно большой 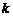 -го порядка и записывают это так:
-го порядка и записывают это так: 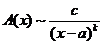 . (Знак ~ читается «асимптотически равно»).
. (Знак ~ читается «асимптотически равно»).
