Предел монотонной последовательности
Предел монотонной последовательности
Определение. Последовательность  называется
называется
- монотонно возрастающей (неубывающей), если 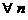
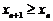 ;
;
- строго монотонно возрастающей (неубывающей), если 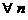
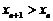 ;
;
- монотонно убывающей (невозрастающей), если 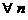
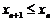 ;
;
- строго монотонно убывающей (невозрастающей), если 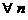
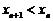 ;
;
Монотонно возрастающие последовательности обозначают символом 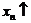 , монотонно убывающие - символом
, монотонно убывающие - символом 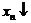 .
.
Сейчас докажем одну из важнейших теорем.
Теорема
1. Если последовательность  монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу;
монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу;
2. Если последовательность  монотонно возрастает, но неограниченна сверху, то
монотонно возрастает, но неограниченна сверху, то 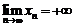 .
.
Доказательство.
Часть 1. Пусть 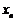 ограниченны сверху, то есть
ограниченны сверху, то есть 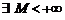 такое, что
такое, что 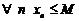 . Тогда, согласно теореме о существовании супремума мы можем утверждать, что
. Тогда, согласно теореме о существовании супремума мы можем утверждать, что 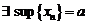 .
.
Вспомним свойства 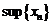 . Их было два
. Их было два
1. 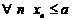 ;
;
2. 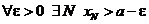 .
.
Но учтем теперь что 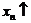 . Это значит, что
. Это значит, что 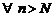
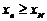 . Тогда имеем следующую цепочку неравенств
. Тогда имеем следующую цепочку неравенств 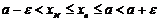 .
.
Выбрасывая лишнее, получим, что 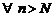
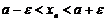 или
или 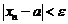 , что и говорит о том, что
, что и говорит о том, что 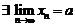 .
.
Заметьте, что предел равен как раз супремуму множества  .
.
Часть 2.Пусть теперь 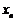 неограниченна сверху. Это значит, что
неограниченна сверху. Это значит, что 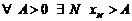 .
.
Но 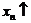 . Значит,
. Значит, 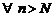
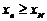 и поэтому можно записать
и поэтому можно записать 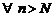
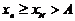 . Выбрасывая в этом неравенстве
. Выбрасывая в этом неравенстве 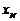 , получим окончательно
, получим окончательно
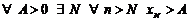 ,
,
что и говорит о том, что 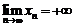 . <
. <
Лемма о вложенных отрезках
Определение 1. Множество, элементами которого являются отрезки, называется системой отрезков.
Определение 2. Система замкнутых отрезков 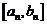 называется стягивающей, если
называется стягивающей, если
1. 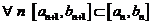 то есть каждый последующий отрезок расположен внутри предыдущего;
то есть каждый последующий отрезок расположен внутри предыдущего;
2. 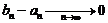 , то есть длины отрезков стремятся к нулю.
, то есть длины отрезков стремятся к нулю.
Возникающая ситуация изображена на рисунке
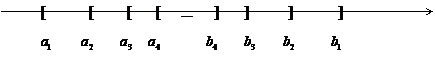
Лемма о вложенных отрезках
Для любой системы замкнутых стягивающихся отрезков существует единственная точка, принадлежащая всем отрезкам.
Доказательство.
1. Рассмотрим множество 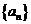 левых концов наших отрезков. Очевидно, что
левых концов наших отрезков. Очевидно, что
а) 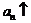 ,
,
б) 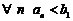 .
.
Поэтому, по предыдущей теореме, существует конечный 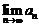 .
.
2. Рассмотрим множество 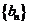 правых концов наших отрезков. Очевидно, что
правых концов наших отрезков. Очевидно, что
а) 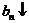 ,
,
б) 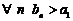 .
.
Поэтому существует конечный 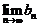 .
.
3. Так как по условию 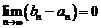 , то
, то 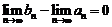 и, следовательно,
и, следовательно, 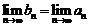 .
.
Обозначим этот общий предел через 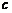 :
: 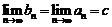
4. Так как 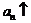 а
а 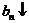 , то, очевидно, что
, то, очевидно, что 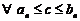 , то есть точка
, то есть точка 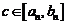
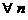 ; (она принадлежит всем отрезкам сразу)
; (она принадлежит всем отрезкам сразу)
5. Докажем, что точка 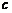 единственная.
единственная.
Предположим противное: что 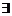 точка
точка 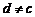 , такая что
, такая что 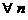
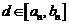 . Но тогда было бы, что
. Но тогда было бы, что 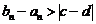 , что противоречит тому, что
, что противоречит тому, что 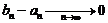 .
.
Отметим одну деталь: мы доказали не только существование точки 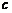 , принадлежащей всем отрезкам, но и то, что
, принадлежащей всем отрезкам, но и то, что 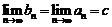 . Это будет нам надо в дальнейшем. <
. Это будет нам надо в дальнейшем. <
2.7 Число 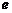
Прежде чем переходить к знаменитому в математике числу 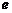 , дадим без вывода одну полезную формулу, которая называется биномом Ньютона.
, дадим без вывода одну полезную формулу, которая называется биномом Ньютона.
Напомним, что 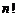 (читается: n-факториал) есть произведение целых чисел от 1 до
(читается: n-факториал) есть произведение целых чисел от 1 до 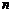
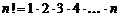 .
.
По определению считается 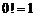 .
.
Выражение 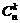 (читается
(читается 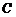 из
из 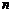 по
по 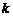 )
)
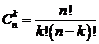 .
.
называется биноминальным коэффициентом. Другое выражение для 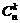 имеет вид
имеет вид
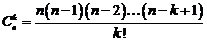 .
.
В частности 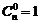 ,
, 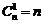 ,
, 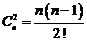 и т.д.
и т.д.
Бином Ньютона имеет вид
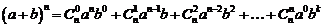
или в более явном виде
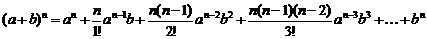 .
.
Отсюда легко получаются известные из школьного курса выражения для 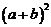 ,
, 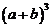 ,
, 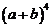 и т.д.
и т.д.
Рассмотрим теперь последовательность  с членами
с членами 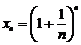 ,
, 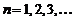 .
.
1. Получим другое выражение для 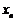 .
.
Используя формулу бинома Ньютона, получим 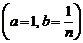 .
.
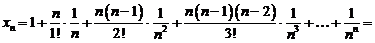
= 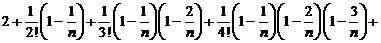
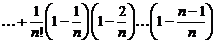 .
.
2. Покажем, что  .
.
Для этого запишем рядом 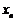 и
и 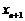 .
.
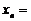
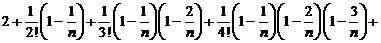
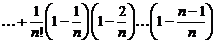 ;
;
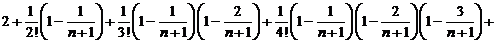
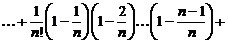
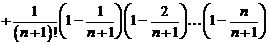 .
.
Так как 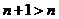 , то
, то 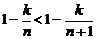 ,
, 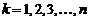 . Поэтому каждое слагаемое в
. Поэтому каждое слагаемое в 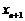 больше соответствующего слагаемого в
больше соответствующего слагаемого в 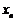 . Кроме того, в
. Кроме того, в 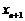 есть «лишнее» положительное слагаемое
есть «лишнее» положительное слагаемое 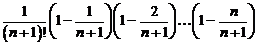 , которого не было в
, которого не было в 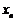 . Поэтому
. Поэтому 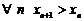 .
.
3. Покажем теперь, что 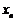 ограничена сверху.
ограничена сверху.
Действительно, так как 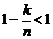 , то
, то
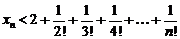 .
.
Но так как
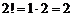
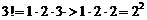 ,
,
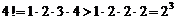 ,
,
и вообще 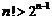 , то
, то 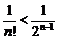 и
и
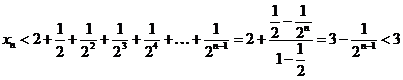 ,
,
где в процессе выкладок использована формула для суммы геометрической прогрессии.
Итак, 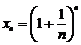 монотонно возрастает и
монотонно возрастает и 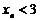 . Поэтому существует
. Поэтому существует 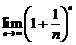 , который и называется числом е
, который и называется числом е
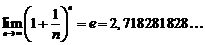 .
.
Это число чрезвычайно популярно в математике и в дальнейшем будет постоянно встречаться.
2.8 Подпоследовательности
Пусть 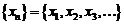 - некоторая последовательность.
- некоторая последовательность.
Пусть 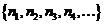 есть также последовательность, у которой
есть также последовательность, у которой
а) все 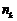 - целые положительные числа;
- целые положительные числа;
б) 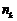 монотонно возрастает с ростом
монотонно возрастает с ростом 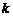 ;
;
в) 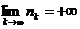 .
.
Рассмотрим теперь последовательности вида 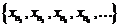 , которая представляет собой «кусочек» исходной последовательности
, которая представляет собой «кусочек» исходной последовательности  и которая получается из нее оставлением членов с номерами
и которая получается из нее оставлением членов с номерами 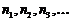 . Она называется подпоследовательностью последовательности
. Она называется подпоследовательностью последовательности  .
.
Пример. Пусть 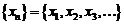 . Рассмотрим последовательность {1, 4, 9, 16, 25, …}. Тогда {x1, x4, x9, x16, x25, … } - подпоследовательность исходной последовательности
. Рассмотрим последовательность {1, 4, 9, 16, 25, …}. Тогда {x1, x4, x9, x16, x25, … } - подпоследовательность исходной последовательности  .
.
Из многочисленных свойств подпоследовательности мы рассмотрим лишь два.
Теорема.
1. Если последовательность  сходится, то любая ее подпоследовательность тоже сходится к тому же самому пределу.
сходится, то любая ее подпоследовательность тоже сходится к тому же самому пределу.
2. Если последовательность  , то любая ее подпоследовательность тоже бесконечно большая.
, то любая ее подпоследовательность тоже бесконечно большая.
Доказательство.
1. В данном доказательстве будет использован формальный прием преобразования строчек кванторов, который необходимо освоить, так как в дальнейшем он будет часто использоваться.
Итак, пусть исходная последовательность сходящаяся. Имеем
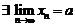 Þ
Þ 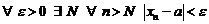 ,
,
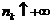 Þ
Þ 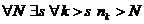 .
.
Совершим «прогулку» по этим строкам кванторов по следующему маршруту
"e>0 ® $N ® "N ® $s ®"k>s ® nk>N ® "nk>N ® |xn-a|<e
указанному стрелками. Тогда комбинация кванторов  «взаимно уничтожается». Оставляя лишь подчеркнутые кванторы, получим
«взаимно уничтожается». Оставляя лишь подчеркнутые кванторы, получим
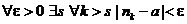 ,
,
что по определению означает, что 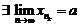 .
.
2. Пусть теперь исходная последовательность бесконечно большая. Тогда имеем
{xn} - б.б.п. Þ 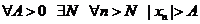 ,
,
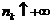 Þ
Þ 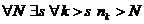 .
.
Совершим «прогулку» по этим строкам кванторов по следующему маршруту
"А > 0 ® $N ®"N ® $s ®"k>s ® nk>N ® "nk>N ® |xn| > A.
Оставляя лишь подчеркнутые кванторы, получим
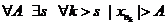 ,
,
откуда, по определению, и следует, что 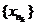 - б.б.п. <
- б.б.п. <
А теперь знаменитая
лемма Больцано - Вейерштрасса. Из любой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.
Из любой неограниченной последовательности можно выбрать бесконечно большую подпоследовательность.
Доказательство.
Часть 1.При доказательстве этой леммы использован широко применяемый прием - «деление отрезка пополам».
Итак, пусть некоторая последовательность  ограничена, то есть
ограничена, то есть 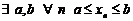 . Это означает, что все члены
. Это означает, что все члены 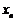 последовательности
последовательности  лежат на отрезке
лежат на отрезке 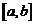 .
.
Предел монотонной последовательности
Определение. Последовательность  называется
называется
- монотонно возрастающей (неубывающей), если 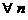
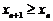 ;
;
- строго монотонно возрастающей (неубывающей), если 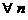
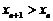 ;
;
- монотонно убывающей (невозрастающей), если 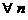
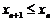 ;
;
- строго монотонно убывающей (невозрастающей), если 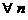
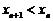 ;
;
Монотонно возрастающие последовательности обозначают символом 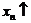 , монотонно убывающие - символом
, монотонно убывающие - символом 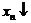 .
.
Сейчас докажем одну из важнейших теорем.
Теорема
1. Если последовательность  монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу;
монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу;
2. Если последовательность  монотонно возрастает, но неограниченна сверху, то
монотонно возрастает, но неограниченна сверху, то 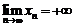 .
.
Доказательство.
Часть 1. Пусть 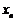 ограниченны сверху, то есть
ограниченны сверху, то есть 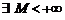 такое, что
такое, что 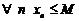 . Тогда, согласно теореме о существовании супремума мы можем утверждать, что
. Тогда, согласно теореме о существовании супремума мы можем утверждать, что 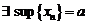 .
.
Вспомним свойства 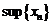 . Их было два
. Их было два
1. 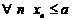 ;
;
2. 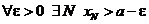 .
.
Но учтем теперь что 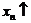 . Это значит, что
. Это значит, что 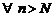
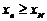 . Тогда имеем следующую цепочку неравенств
. Тогда имеем следующую цепочку неравенств 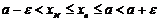 .
.
Выбрасывая лишнее, получим, что 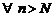
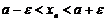 или
или 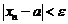 , что и говорит о том, что
, что и говорит о том, что 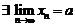 .
.
Заметьте, что предел равен как раз супремуму множества  .
.
Часть 2.Пусть теперь 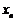 неограниченна сверху. Это значит, что
неограниченна сверху. Это значит, что 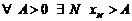 .
.
Но 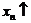 . Значит,
. Значит, 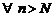
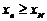 и поэтому можно записать
и поэтому можно записать 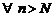
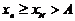 . Выбрасывая в этом неравенстве
. Выбрасывая в этом неравенстве 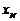 , получим окончательно
, получим окончательно
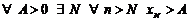 ,
,
что и говорит о том, что 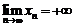 . <
. <
Лемма о вложенных отрезках
Определение 1. Множество, элементами которого являются отрезки, называется системой отрезков.
Определение 2. Система замкнутых отрезков 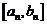 называется стягивающей, если
называется стягивающей, если
1. 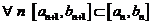 то есть каждый последующий отрезок расположен внутри предыдущего;
то есть каждый последующий отрезок расположен внутри предыдущего;
2. 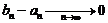 , то есть длины отрезков стремятся к нулю.
, то есть длины отрезков стремятся к нулю.
Возникающая ситуация изображена на рисунке
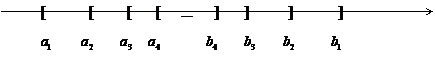
Лемма о вложенных отрезках
Для любой системы замкнутых стягивающихся отрезков существует единственная точка, принадлежащая всем отрезкам.
Доказательство.
1. Рассмотрим множество 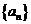 левых концов наших отрезков. Очевидно, что
левых концов наших отрезков. Очевидно, что
а) 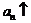 ,
,
б) 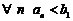 .
.
Поэтому, по предыдущей теореме, существует конечный 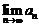 .
.
2. Рассмотрим множество 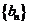 правых концов наших отрезков. Очевидно, что
правых концов наших отрезков. Очевидно, что
а) 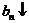 ,
,
б) 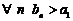 .
.
Поэтому существует конечный 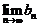 .
.
3. Так как по условию 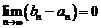 , то
, то 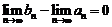 и, следовательно,
и, следовательно, 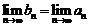 .
.
Обозначим этот общий предел через 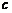 :
: 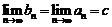
4. Так как 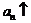 а
а 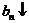 , то, очевидно, что
, то, очевидно, что 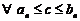 , то есть точка
, то есть точка 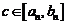
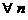 ; (она принадлежит всем отрезкам сразу)
; (она принадлежит всем отрезкам сразу)
5. Докажем, что точка 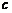 единственная.
единственная.
Предположим противное: что 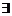 точка
точка 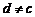 , такая что
, такая что 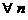
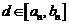 . Но тогда было бы, что
. Но тогда было бы, что 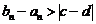 , что противоречит тому, что
, что противоречит тому, что 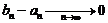 .
.
Отметим одну деталь: мы доказали не только существование точки 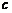 , принадлежащей всем отрезкам, но и то, что
, принадлежащей всем отрезкам, но и то, что 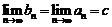 . Это будет нам надо в дальнейшем. <
. Это будет нам надо в дальнейшем. <
2.7 Число 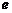
Прежде чем переходить к знаменитому в математике числу 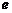 , дадим без вывода одну полезную формулу, которая называется биномом Ньютона.
, дадим без вывода одну полезную формулу, которая называется биномом Ньютона.
Напомним, что 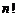 (читается: n-факториал) есть произведение целых чисел от 1 до
(читается: n-факториал) есть произведение целых чисел от 1 до 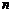
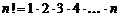 .
.
По определению считается 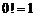 .
.
Выражение 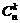 (читается
(читается 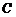 из
из 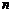 по
по 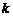 )
)
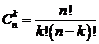 .
.
называется биноминальным коэффициентом. Другое выражение для 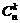 имеет вид
имеет вид
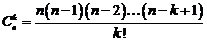 .
.
В частности 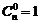 ,
, 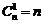 ,
, 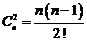 и т.д.
и т.д.
Бином Ньютона имеет вид
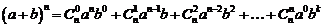
или в более явном виде
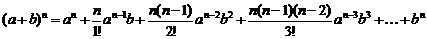 .
.
Отсюда легко получаются известные из школьного курса выражения для 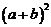 ,
, 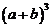 ,
, 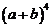 и т.д.
и т.д.
Рассмотрим теперь последовательность  с членами
с членами 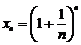 ,
, 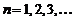 .
.
1. Получим другое выражение для 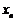 .
.
Используя формулу бинома Ньютона, получим 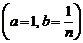 .
.
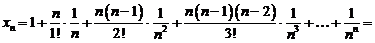
= 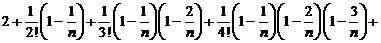
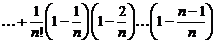 .
.
2. Покажем, что 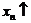 .
.
Для этого запишем рядом  и
и 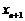 .
.
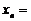
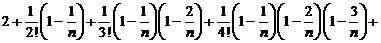
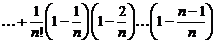 ;
;
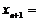
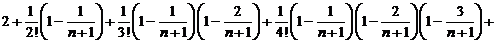
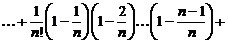
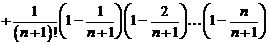 .
.
Так как 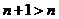 , то
, то 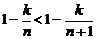 ,
, 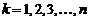 . Поэтому каждое слагаемое в
. Поэтому каждое слагаемое в 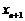 больше соответствующего слагаемого в
больше соответствующего слагаемого в 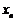 . Кроме того, в
. Кроме того, в 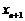 есть «лишнее» положительное слагаемое
есть «лишнее» положительное слагаемое 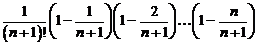 , которого не было в
, которого не было в 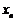 . Поэтому
. Поэтому 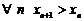 .
.
3. Покажем теперь, что 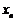 ограничена сверху.
ограничена сверху.
Действительно, так как 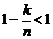 , то
, то
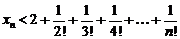 .
.
Но так как
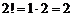
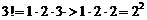 ,
,
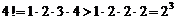 ,
,
и вообще 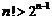 , то
, то 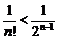 и
и
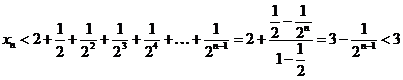 ,
,
где в процессе выкладок использована формула для суммы геометрической прогрессии.
Итак, 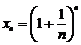 монотонно возрастает и
монотонно возрастает и 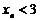 . Поэтому существует
. Поэтому существует 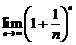 , который и называется числом е
, который и называется числом е
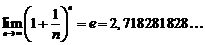 .
.
Это число чрезвычайно популярно в математике и в дальнейшем будет постоянно встречаться.
2.8 Подпоследовательности
Пусть 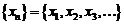 - некоторая последовательность.
- некоторая последовательность.
Пусть 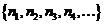 есть также последовательность, у которой
есть также последовательность, у которой
а) все 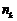 - целые положительные числа;
- целые положительные числа;
б) 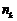 монотонно возрастает с ростом
монотонно возрастает с ростом 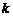 ;
;
в) 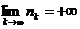 .
.
Рассмотрим теперь последовательности вида 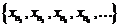 , которая представляет собой «кусочек» исходной последовательности
, которая представляет собой «кусочек» исходной последовательности  и которая получается из нее оставлением членов с номерами
и которая получается из нее оставлением членов с номерами 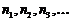 . Она называется подпоследовательностью последовательности
. Она называется подпоследовательностью последовательности  .
.
Пример. Пусть 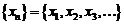 . Рассмотрим последовательность {1, 4, 9, 16, 25, …}. Тогда {x1, x4, x9, x16, x25, … } - подпоследовательность исходной последовательности
. Рассмотрим последовательность {1, 4, 9, 16, 25, …}. Тогда {x1, x4, x9, x16, x25, … } - подпоследовательность исходной последовательности  .
.
Из многочисленных свойств подпоследовательности мы рассмотрим лишь два.
Теорема.
1. Если последовательность  сходится, то любая ее подпоследовательность тоже сходится к тому же самому пределу.
сходится, то любая ее подпоследовательность тоже сходится к тому же самому пределу.
2. Если последовательность  , то любая ее подпоследовательность тоже бесконечно большая.
, то любая ее подпоследовательность тоже бесконечно большая.
Доказательство.
1. В данном доказательстве будет использован формальный прием преобразования строчек кванторов, который необходимо освоить, так как в дальнейшем он будет часто использоваться.
Итак, пусть исходная последовательность сходящаяся. Имеем
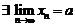 Þ
Þ 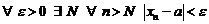 ,
,
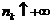 Þ
Þ 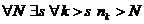 .
.
Совершим «прогулку» по этим строкам кванторов по следующему маршруту
"e>0 ® $N ® "N ® $s ®"k>s ® nk>N ® "nk>N ® |xn-a|<e
указанному стрелками. Тогда комбинация кванторов 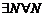 «взаимно уничтожается». Оставляя лишь подчеркнутые кванторы, получим
«взаимно уничтожается». Оставляя лишь подчеркнутые кванторы, получим
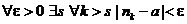 ,
,
что по определению означает, что 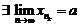 .
.
2. Пусть теперь исходная последовательность бесконечно большая. Тогда имеем
{xn} - б.б.п. Þ 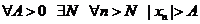 ,
,
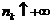 Þ
Þ 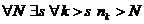 .
.
Совершим «прогулку» по этим строкам кванторов по следующему маршруту
"А > 0 ® $N ®"N ® $s ®"k>s ® nk>N ® "nk>N ® |xn| > A.
Оставляя лишь подчеркнутые кванторы, получим
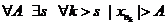 ,
,
откуда, по определению, и следует, что 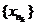 - б.б.п. <
- б.б.п. <
А теперь знаменитая
лемма Больцано - Вейерштрасса. Из любой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.
Из любой неограниченной последовательности можно выбрать бесконечно большую подпоследовательность.
Доказательство.
Часть 1.При доказательстве этой леммы использован широко применяемый прием - «деление отрезка пополам».
Итак, пусть некоторая последовательность  ограничена, то есть
ограничена, то есть 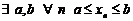 . Это означает, что все члены
. Это означает, что все члены 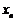 последовательности
последовательности  лежат на отрезке
лежат на отрезке 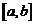 .
.
