Логарифмическое дифференцирование.

Принимается для диф-ния степенно-показательных ф-ций, т.е. вида y=f(x)^g(x), а также сложных, но удобных для логарифмирования (например для нахождения производной произведения нескольких функций). Для этого нужно прологарифмировать обе части функции, а затем просто выразить из результата y’.

Производные высших порядков.

Пусть ф-ция y=f(x) дифф-ма, т.е. сущ-ет f’(x). Т.к. f’(x) – ф-ция от х, то ее также можно продиф-ть, т.е. от нее взять производную.

Производная от производной ф-ции, если она сущ-ет, наз пр-ной 2-го порядка(2-я пр-ная) и обозначается y’’.

f’’(x)=(f’(x))’ =lim(∆x→0) (f’(x+∆x)-f’(x))/∆x

Произв-я от произв-ной (n-1)-го порядка наз производной n-го порядка, обозначается

f⁽ⁿ⁾(x)=(f^(n-1)(x))’ =lim(∆x→0) (f^(n-1)(x+∆x)-f^(n-1)(x))/∆x

Правила дифф-ния соотв-ют осн правилам дифф-ния.

Производн. ф-ий заданных неявно

У=f(x)-явная. F(x;y)=0 (1) неявная ф-ия. y_x’-?

Для нахождения y_x надо диф-ть (1) по переменным х и у. рассматривая при этом у как сложную ф-ию от х т.е. домножая на y_x’. В полученном выражении находим подобные члены содержащие y_x’ и решая его как Ур-е найдем y_x’.

Произ-ие ф-ий заданных параметрически

Y=f(x) задана

{X=z(t),y=h(t),

z,h-диф-уемы по параметру t, z_t’ не равен 0

Пусть для x=z(t) существует ф-ия t=g(x);

Y=f(x) – сложная функция

{y=h(t), t=g(x) то

y’=h’(t)*g’(x), но по правилу 5

{5. y=f(x) и x=g(y) – взаимно-обратные ф-ции, то y_x'=1/x_y'}

g’(x)=1/z’(t)

Y_x’=Y_t’/X_t’=F(t)

Y_xx’’=F’(t)/X’t

Ур.кас-ой. нормали.

Касательная - предельное положение секущей.

Нормаль-прямая, перпендик. касательной в точке. Геом.смысл производной

f’(x)=tgA=K

Из аналит.геом

Ур.кос:y-y0=f’(x0)(x-x0) K=-1/f’(x0)

Ур.нормали y-y0=-(x-x0)/f’(x0)

Дифференциал функции

У=f(x) - диф-ма. т. е. сущ-т f’(x)=Lim(Δx→0)ΔY/ΔX

В силу основной теоремы о пределах имеем:

Δy/Δx=f ’(x)+α(Δx) (α(Δx)→0 когда Δx→0)

Δy=f’(x)Δx+ α(Δx)Δx

f’(x)Δx-гл.часть приращения Δy наз-ся диф-ом функции. dy=f ’(x) Δx

Если у=х то dx=Δx dy=f ’(x)dx

Δy=dy+ αΔx

Δy≈dy f’(x)=dy/dx

f(x)-f(x0) ≈ f ’(x0)Δx

f(x) ≈ f(x0)+f’(x0)Δx

геометрич. смысл

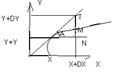tg(α)=f’(x)

TN=tgαΔx=f ’(x)dx=dy, MN = Δy

{на графике ВМЕСТО X+DX надо писать X+ΔX!}

Т.о.диф-л ф-ии y=f(x) в т.Х есть приращение ординаты касательной приведенный к графику ф-ии y=f(x) в точке (x;f(x))

Св-ва диф-ов: d(u+v)=du+dv

d(uv)=udv+vdu

d(u/v)=(vdu-udv)/v²

Диф-ы высших порядков

Рассм. дифференциал функции:

dy=f ‘(x)dx. Опр. Диф-лом (n)-го порядка наз. дифференциал от дифференциала (n-1)-го порядка

d(d^(n-1)y)=d⁽ⁿ⁾y

d²y=d(dy)=d(f’(x)dx)=(f’(x)dx)’dx=f’’(x)dx²

Диф-ал n-го порядка равен:

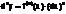
Диф-ы сложных ф-ий

Расм. Сложную ф-ию

{y=f(u),u=g(x)}

Y=f(g(x))=F(x)

dy=F’(x)dx=f’

(u)g’(x)dx=f’(u)du

Св.инвариантности: диф-л 1-го порядка сохр. свою форму независимо от того будет ли аргумент ф-ии независимой переменной или функцией.

Для диф-в высшего порядка это св-во не сохраняется

Правило Лопиталя

используется для нахождения пределов отношений вида 0/0 ∞/∞

Limf(x)/g(x)= f(a)/g(a)=0/0-?;

Limf(x)/g(x)= ∞/∞-?

Т1. Пусть заданы дифференцируемые ф-ии f(x) и g(x) на отрезке [а;b] и f(a)=g(a)=0,то при существовании предела Lim(f(x)/g(x))= Lim(f’(x)/g’(x))

Предел отношения ф-ии равен пределу отношения их производных.

Д-во: т.к. ф-ии диф-емы то к ним применим теорему Коши

f(a)=g(a)=0

[f(x)-f(a)]/[g(x)-g(a)]=f’(ξ)/g’(ξ), →сущ-т т.a<ξ<x если x→a то ξ→a. расм.

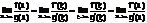
Монотонность ( возр и убыв ф-ии) теорема:

Пусть y=f(x) диф-ма на[ab] тогда если f’(x)>0 то функция возрастает, иначе - убывает

правилo:

1D(x)? 2.f’(x)?

3.f’(x)=0 (находим корни)?

4. Смотрим где че убывает/возрастает

5. Пишем ответ ответ.