Экстремумы функции одной переменной. Необходимое и достаточные условия экстремума.

Точка х0-наз-ся т. max ф-ии y=f(x) если f(x0)>f(x) для любого х в окрестности т.х0

Необх. условие экстремум

Если ф-ия y=f(x) непрерывна и имеет в т. х0 экстремум то f’(x0)=0 или f’(x0) не сущ-т

Условие необходимое, но не достаточное.

{для примера рассм функцию f(x)=x³}

Точки на D(y) где f’(x)=0 или не сущ Наз-ся критическими

Дост. признак экстремума

Пусть т. Х0-критическая (f’(x0)=0, несущ.) если

Правило нахождения экстремума

1. D(x)? 2.f’(x)?

3. крит точки?

4. разбить D(f) точками (+-)

5. Ответ

Дост. признак экстремума

Пустьf’(x0)=0, f’’(x0)≠0 то если f’’(x0)<0 то x0-т.max, f’’(x0)>0 то x0-т.min

Выпуклость и вогнутость, точки перегиба.

График дифференцируемый на [a;b] наз-ся вып(вогн) если он расположен ниже(выше) любой своей касательной

Теорема (признак вып и вогн-и графика)

Если f’’(x)<0 для любого х на[a b] То граф.ф-и вып

f’’(x)>0для любого х на [ab] то граф ф-и вог.

Точка графика непрерывной ф-ии отделяющая ее выпуклость от вогнутости наз-ся т.перегиба

Необходимый признак т. перегиба

Если т.х0 является т. перегиба графика ф-ии y=f(x) то f’’(x0)=0 или несущ.

Достаточный признак т.перегиба

Если при переходе через т.х0 f”(x0) меняет знак то (x0;f(x0))-т.перегиба графика непрервн. ф-ии y=f(x)

Асимптоты графика ф-ии. Полное исследование.

Прямая линия наз-ся асимптотой графика ф-ии y=f(x) если расстояние от переменной точки графика до этой прямой стремится к нулю при неограниченном удалении точки от начала координат.

{ко всем асимптотам нужны графики!}

Вертикальные асимптоты

-

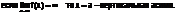Наклонная асимптота

Прямая y=kx+b-накл.ассимп графика ф-ии y=f(x) если

f(x)-kx-b→0, т. к. по формуле нахождения расстояния от точки то графика

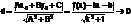
Теорема

Для того чтоб прямая y=kx+b была наклон асимп.грфика ф-ии y=(x) необходимо и достаточно чтобы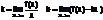

Горизонтальная

Если при нахождении накл.ас. к=0 то y=b- г.о.

28 Первообразная, неопределенный интеграл, его свойства, таблица интегралов.

Ф-ция F(x) называется первообразной для f(x) на некотором интервале. F’(x)=f(x)

Теорема. Если ф-ция f(x) имеет хотя бы одну первообразную F(x),то ф-ция F(x)+C также является первообразной f(x).

Совокупность всех первообразных для f(x) назыв. неопределенным интегралом от этой ф-ции и

обозначается. ∫f(x)dx=F(x)+C f(x)-подынтегральная ф-ция, f(x)dx- подынтегральное выражение.

Свойства. 1) (∫f(x)dx)’=(F(x)+C)’=F’(x)=f(x)

2) d∫f(x)dx =(∫f(x)dx)’dx=f(x)dx

3) ∫df(x)dx=∫f’(x)dx =f(x)+C

Теорема. Если f(x) непрерывна на интервале (а,b),то она имеет на нем первообразную.

Геометрический смысл первообразной. ∫f(x)dx =F(x)+C=y эти уравнения определяют множества кривых, которые назыв. интегральными кривыми. Для того чтобы выделить из семейства интегральных кривых одну, задают начальные условия, что равносильно заданию точки, через которую проходит искомая интегральная кривая.

Методы интегрирования:метод разложения,метод замены переменной.

1)∫f1(x)+f2(x)dx=∫f1(x)dx+∫f2(x)dx

2)∫Cf(x)dx=C∫f(x)dx

3)Если ∫f(x)dx=F(x)+C ,то ∫f(u)du =F(u)+C , где u=φ(x)

I. ∫λ₁f₁(x)+…+λ_nf_n(x)dx= λ₁∫f₁(x)dx+ λ_n∫f_n(x)dx

II. Метод замены переменной

∫f(x)dx=|x=φ(t), dx=φ’(t)dt|=∫f(φ(t))φ’(t)dt