Свойства собственных векторов
1. Любая линейная комбинация собственных векторов, отвечающих одному и тому же собственному числу, является также собственным вектором с тем же собственным числом.
2. Если собственные векторы 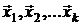 отвечают попарно различным собственным числам λ1, λ2, … , λk, то система векторов
отвечают попарно различным собственным числам λ1, λ2, … , λk, то система векторов 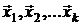 линейно независима.
линейно независима.
3. Собственные числа линейного оператора А : V → W не изменяются при изменении базиса.
Пример:
Найти собственные значения и собственные векторы для матрицы
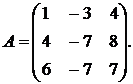
Решение:составим характеристическое уравнение
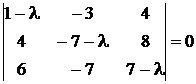 .
.
Вычисляя этот определитель, получим (λ + 1)2(λ – 3) = 0, λ1 = –1, λ2 = 3.
Система для определения собственного вектора, соответствующего собственному значению λ2 = 3 имеет вид:
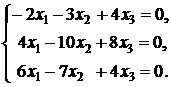
Третье уравнение равно разности второго и первого, поэтому его можно вычеркнуть из системы. Получим систему 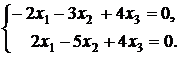
В качестве свободной неизвестной величины можно выбрать х3 и выразить через неё неизвестные х1 и х2. Получим
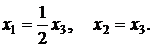
Полагая х3 = 2, найдем собственный вектор 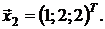
Аналогично найдём собственный вектор, соответствующий собственному числу λ1 = –1, 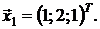
Заметим, что собственному числу λ1 = –1 кратности 2 соответствует лишь один с точностью до постоянного множителя собственный вектор, так как в рассматриваемом примере rang(A – λT) = 2 при λ = –1. Таким образом, матрица А имеет лишь два линейно независимых собственных вектора.
Задания для самостоятельной работы
1.Найти длину и направляющие косинусы вектора:
1.1. 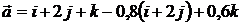 . 1.2.
. 1.2. 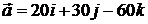 .
.
2. Найти орт вектора:
2.1. 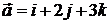 . 2.2.
. 2.2. 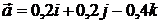 . 2.3.
. 2.3. 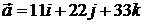 .
.
3. Образуют ли трапецию точки А(3;–1;2), В(1;2; –1), С(–1;1; –3), D(3; –5;3)?
4. Точки А, В, С, D – вершины параллелограмма. Точка О – точка пересечения его диагоналей (его центр). Найти разложение векторов 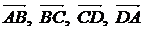 по векторам
по векторам 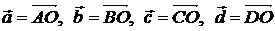 .
.
5. Вычислить скалярное произведение векторов:
5.1. 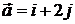 и
и 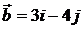 . 5.2.
. 5.2. 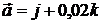 и
и 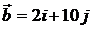 . 5.3.
. 5.3. 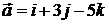 и
и 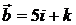 .
.
6. Найти пр 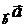 и пр
и пр 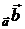 :
:
6.1 . 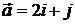 ,
, 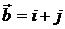 . 6.2.
. 6.2. 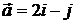 ,
, 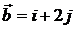 . 6.3.
. 6.3. 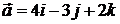 ,
, 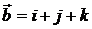 .
.
7. Вычислить векторное произведение векторов:
7.1. 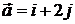 и
и 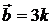 . 7.2.
. 7.2. 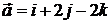 ,
, 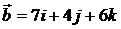 . 7.3.
. 7.3. 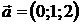 ,
, 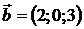 .
.
8. Найти синус угла между векторами:
8.1. 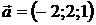 и
и 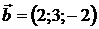 . 8.2.
. 8.2. 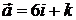 и
и 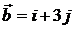 . 8.3.
. 8.3. 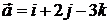 и
и 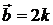 .
.
9. Указать левой или правой тройкой являются векторы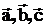 :
:
9.1. 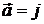 ,
, 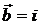 ,
, 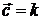 . 9.2.
. 9.2. 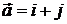 ,
, 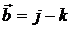 ,
, 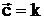 . 9.3.
. 9.3. 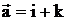 ,
, 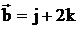 ,
, 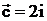 .
.
10. Компланарны ли векторы:
10.1. 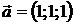 ,
, 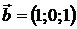 ,
, 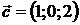 . 10.2.
. 10.2. 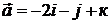 ,
, 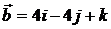 ,
, 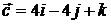 .
.
11. Найти объём тетраэдра построенного на векторах 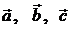 :
:
11.1. 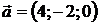 ,
, 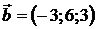 ,
, 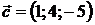 . 11.2.
. 11.2. 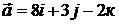 ,
, 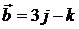 ,
, 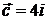 .
.
12. Найти собственные числа и собственные векторы линейного оператора, заданного матрицей
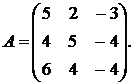
13.Показать, что собственные векторы матрицы 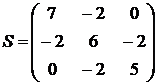 ортогональны.
ортогональны.
Ответы
1.1. 1,66; 0,12; 0,24; 0,96. 1.2. 70; 2/7;3/7;-6/7. 2.1. 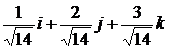 . 2.2.
. 2.2. 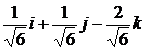 . 2.3. 0,27i +0,53j +0,80k. 3. Да. 4.
. 2.3. 0,27i +0,53j +0,80k. 3. Да. 4. 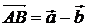 ;
; 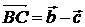 ;
; 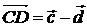 ;
; 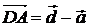 . 5.1. –5. 5.2. 10. 5.3. 0. 6.1. пр
. 5.1. –5. 5.2. 10. 5.3. 0. 6.1. пр 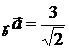 , пр
, пр 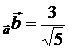 . 6.2. пр
. 6.2. пр 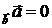 , пр
, пр 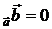 . 6.3. пр
. 6.3. пр 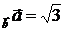 , пр
, пр 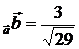 . 7.1. 6i – 3j. 7.2. 20i – 20j – 10k. 7.3. (3;4;-2). 8.1. 1. 13.2. (167/185)1/2. 8.3. (5/56)1/2. 9.1. Левая. 9.2. Правая. 9.3. Левая. 10.1. Нет. 10.2. Да. 11.1. 24 куб.ед. 11.2. 2 куб.ед. 12.λ1 = 1, λ2 = 2, λ3= 3.
. 7.1. 6i – 3j. 7.2. 20i – 20j – 10k. 7.3. (3;4;-2). 8.1. 1. 13.2. (167/185)1/2. 8.3. (5/56)1/2. 9.1. Левая. 9.2. Правая. 9.3. Левая. 10.1. Нет. 10.2. Да. 11.1. 24 куб.ед. 11.2. 2 куб.ед. 12.λ1 = 1, λ2 = 2, λ3= 3. 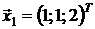 ,
, 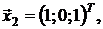
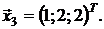 13. λ1 = 9, λ2= 6, λ3 = 3.
13. λ1 = 9, λ2= 6, λ3 = 3.
Вопросы для самоподготовки
1. Векторы.
2. Линейные операции над векторами и их свойства.
3. Линейные пространства. Типы линейных пространств.
4. Чему равна проекция вектора на ось?
5. Координаты вектора в декартовой прямоугольной системе координат. Длина вектора.
6. Коллинеарные векторы. Условие коллинеарности векторов.
7. Скалярное произведение векторов, его свойства.
8. Угол между векторами. Условие перпендикулярности двух векторов.
9. Скалярное произведение векторов в координатной форме.
10. Геометрический и физический смысл скалярного произведения.
11. Евклидово пространство. Норма вектора.
12. Векторное произведение двух векторов.
13. Векторное произведение векторов в координатной форме.
14. Геометрический, физический и механический смысл векторного произведения.
15. Смешанное произведение трех векторов.
16. Смешанное произведение в координатной форме.
17. Геометрический смысл смешанного произведения.
18. Евклидово пространство. Неравенство Коши-Буняковского
19. Определение Линейного оператора.
20. Действия над линейными операторами.
21. Обратный оператор.
22. Собственные векторы и собственные числа.
23. Свойства собственных векторов.
