Матричный метод решения систем линейных уравнений
Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.
Метод удобен для решения систем невысокого порядка.
Метод основан на применении свойств умножения матриц.
Пусть дана система уравнений:
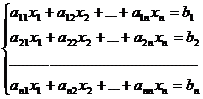
Составим матрицы: A = 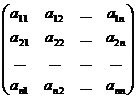 ; B =
; B = 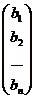 ; X =
; X =  .
.
Систему уравнений можно записать:
A×X = B.
Сделаем следующее преобразование: A-1×A×X = A-1×B,
т.к. А-1×А = Е, то Е×Х = А-1×В
Х = А-1×В
Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.
Пример. Решить систему уравнений:
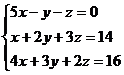
Х = 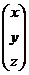 , B =
, B = 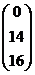 , A =
, A = 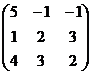
Найдем обратную матрицу А-1.
D = det A = 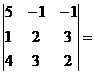 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
M11 = 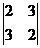 = -5; M21 =
= -5; M21 = 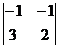 = 1; M31 =
= 1; M31 = 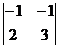 = -1;
= -1;
M12 = 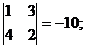 M22 =
M22 = 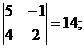 M32 =
M32 = 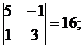
M13 = 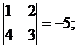 M23 =
M23 = 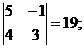 M33 =
M33 = 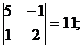
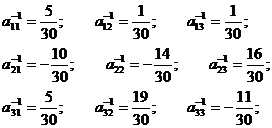 A-1 =
A-1 = 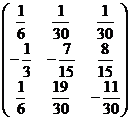 ;
;
Cделаем проверку:
A×A-1 = 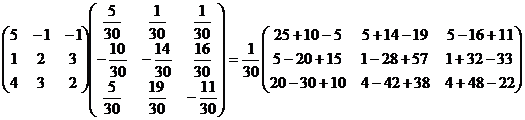 =E.
=E.
Находим матрицу Х.
Х = 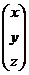 = А-1В =
= А-1В = 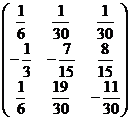 ×
× 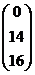 =
= 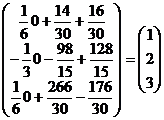 .
.
Итого решения системы: x =1; y = 2; z = 3.
Метод Крамера
Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.
Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.
det A ¹ 0;
Действительно, если какое- либо уравнение системы есть линейная комбинация остальных, то если к элементам какой- либо строки прибавить элементы другой, умноженные на какое- либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
Теорема (Правило Крамера): Система из n уравнений с n неизвестными
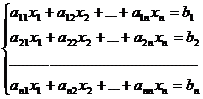
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di/D, где
D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di = 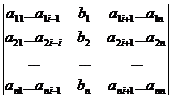
Пример.
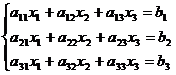
A = 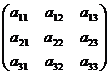 ; D1=
; D1= 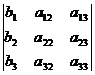 ; D2=
; D2= 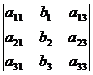 ; D3=
; D3= 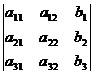 ;
;
x1 = D1/detA; x2 = D2/detA; x3 = D3/detA;
Пример. Найти решение системы уравнений:
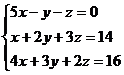
D = 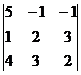 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 = 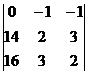 = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30.
x1 = D1/D = 1;
D2 = 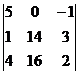 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
x2 = D2/D = 2;
D3 = 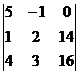 = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x3 = D3/D = 3.
Как видно, результат совпадает с результатом, полученным выше матричным методом.
Решение произвольных систем линейных уравнений
Как было сказано выше, матричный метод и метод Крамера применимы только к тем системам линейных уравнений, в которых число неизвестных равняется числу уравнений. Далее рассмотрим произвольные системы линейных уравнений.
Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
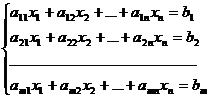 ,
,
где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.
Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.
Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.
Определение. Для системы линейных уравнений матрица
А = 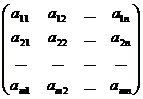 называется матрицей системы, а матрица
называется матрицей системы, а матрица
А*=  называется расширенной матрицей системы
называется расширенной матрицей системы
Определение. Если b1, b2, …,bm = 0, то система называется однородной. однородная система всегда совместна, т.к. всегда имеет нулевое решение.
Элементарные преобразования систем
К элементарным преобразованиям относятся:
1)Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.
2)Перестановка уравнений местами.
3)Удаление из системы уравнений, являющихся тождествами для всех х.
Теорема Кронекера – Капелли
(условие совместности системы)
Теорема:Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
RgA = RgA*.
Очевидно, что система (1) может быть записана в виде:
x1 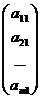 + x2
+ x2 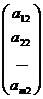 + … + xn
+ … + xn 
Пример. Определить совместность системы линейных уравнений:
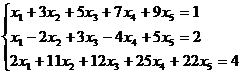
A = 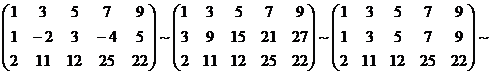
~ 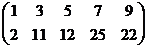 .
. 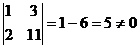 RgA = 2.
RgA = 2.
A* = 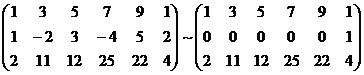 RgA* = 3.
RgA* = 3.
Система несовместна.
Пример. Определить совместность системы линейных уравнений.
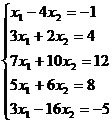 А =
А = 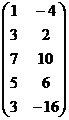 ;
; 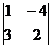 = 2 + 12 = 14 ¹ 0; RgA = 2;
= 2 + 12 = 14 ¹ 0; RgA = 2;
A* = 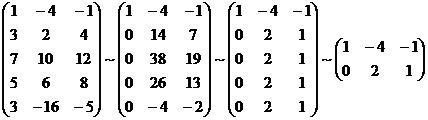
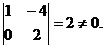 RgA* = 2.
RgA* = 2.
Система совместна. Решения: x1 = 1; x2 =1/2.
Метод Гаусса
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:
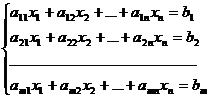
Разделим обе части 1–го уравнения на a11 ¹ 0, затем:
1) умножим на а21 и вычтем из второго уравнения
2) умножим на а31 и вычтем из третьего уравнения
и т.д.
Получим:
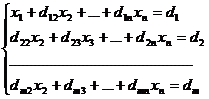 , где d1j = a1j/a11, j = 2, 3, …, n+1.
, где d1j = a1j/a11, j = 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
Пример. Решить систему линейных уравнений методом Гаусса.
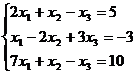
Составим расширенную матрицу системы.
А* = 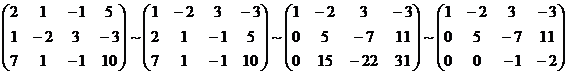
Таким образом, исходная система может быть представлена в виде:
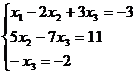 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.
Пример. Решить систему методом Гаусса.
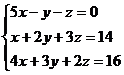
Составим расширенную матрицу системы.
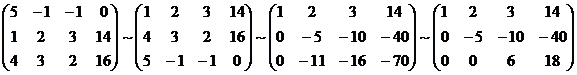
Таким образом, исходная система может быть представлена в виде:
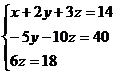 , откуда получаем: z = 3; y = 2; x = 1.
, откуда получаем: z = 3; y = 2; x = 1.
Полученный ответ совпадает с ответом, полученным для данной системы методом Крамера и матричным методом.
Элементы векторной алгебры
Определение. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.
Определение. Длиной (модулем) вектора называется расстояние между началом и концом вектора.
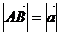
Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.
Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.
Определение. Линейными операциями над векторами называется сложение и умножение на число.
Суммой векторов является вектор - 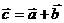
Произведение - 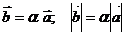 , при этом
, при этом  коллинеарен
коллинеарен  .
.
Вектор  сонаправлен с вектором
сонаправлен с вектором  (
( 
 ), если a > 0.
), если a > 0.
Вектор  противоположно направлен с вектором
противоположно направлен с вектором  (
(  ¯
¯  ), если a < 0.
), если a < 0.
Свойства векторов
1)  +
+  =
=  +
+  - коммутативность.
- коммутативность.
2)  + (
+ (  +
+ 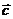 ) = (
) = (  +
+  )+
)+ 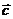
3)  +
+ 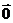 =
= 
4)  +(-1)
+(-1)  =
= 
5) (a×b)  = a(b
= a(b  ) – ассоциативность
) – ассоциативность
6) (a+b)  = a
= a  + b
+ b  - дистрибутивность
- дистрибутивность
7) a(  +
+  ) = a
) = a  + a
+ a 
8) 1×  =
= 
Определение.
1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.
3)Базисом на прямой называется любой ненулевой вектор.
Определение. Если 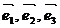 - базис в пространстве и
- базис в пространстве и 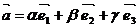 , то числа a, b и g - называются компонентами или координатами вектора
, то числа a, b и g - называются компонентами или координатами вектора  в этом базисе.
в этом базисе.
В связи с этим можно записать следующие свойства:
- равные векторы имеют одинаковые координаты,
- при умножении вектора на число его компоненты тоже умножаются на это число,
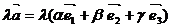 =
= 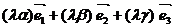 .
.
- при сложении векторов складываются их соответствующие компоненты.
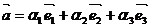 ;
; 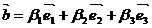 ;
;
 +
+  =
= 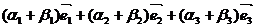 .
.
