Матричный метод решения систем линейных уравнений.
Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.
Метод удобен для решения систем невысокого порядка.
Метод основан на применении свойств умножения матриц.
Пусть дана система уравнений:
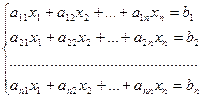
Составим матрицы: A = 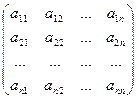 ; B =
; B = 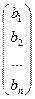 ; X =
; X = 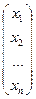 .
.
Систему уравнений можно записать:
A×X = B.
Сделаем следующее преобразование: A-1×A×X = A-1×B,
т.к. А-1×А = Е, то Е×Х = А-1×В
Х = А-1×В
Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.
Пример. Решить систему уравнений:
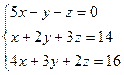
Х = 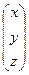 , B =
, B = 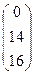 , A =
, A = 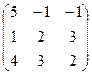
Найдем обратную матрицу А-1.
D = det A = 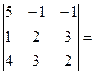 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
M11 = 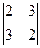 = -5; M21 =
= -5; M21 = 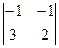 = 1; M31 =
= 1; M31 = 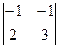 = -1;
= -1;
M12 = 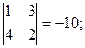 M22 =
M22 = 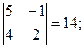 M32 =
M32 = 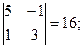
M13 = 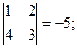 M23 =
M23 = 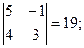 M33 =
M33 = 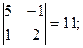
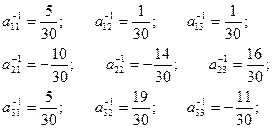 A-1 =
A-1 = 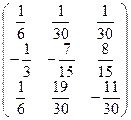 ;
;
Cделаем проверку:
A×A-1 = 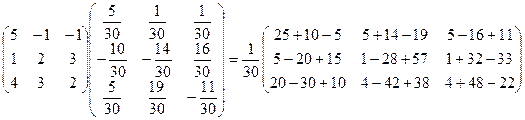 =E.
=E.
Находим матрицу Х.
Х = 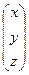 = А-1В =
= А-1В = 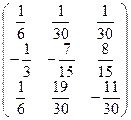 ×
× 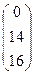 =
= 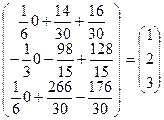 .
.
Итого решения системы: x =1; y = 2; z = 3.
Несмотря на ограничения возможности применения данного метода и сложность вычислений при больших значениях коэффициентов, а также систем высокого порядка, метод может быть легко реализован на ЭВМ.
МЕТОД КРАМЕРА
(Габриель Крамер (1704-1752) швейцарский математик)
Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.
Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.
det A ¹ 0;
Действительно, если какое- либо уравнение системы есть линейная комбинация остальных, то если к элементам какой- либо строки прибавить элементы другой, умноженные на какое- либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
ТЕОРЕМА (ПРАВИЛО КРАМЕРА)
Теорема. Система из n уравнений с n неизвестными
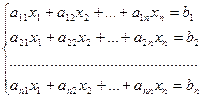
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di/D, где
D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di = 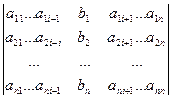
Пример.
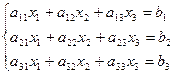
A = 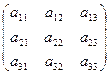 ; D1=
; D1= 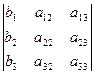 ; D2=
; D2= 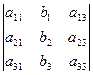 ; D3=
; D3= 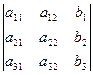 ;
;
x1 = D1/detA; x2 = D2/detA; x3 = D3/detA;
Пример. Найти решение системы уравнений:
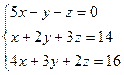
D = 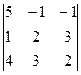 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 = 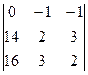 = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30.
x1 = D1/D = 1;
D2 = 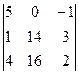 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
x2 = D2/D = 2;
D3 = 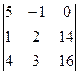 = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x3 = D3/D = 3.
Как видно, результат совпадает с результатом, полученным выше матричным методом.
Если система однородна, т.е. bi = 0, то при D¹0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.
При D = 0 система имеет бесконечное множество решений.
Для самостоятельного решения:
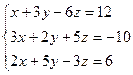 ; Ответ: x = 0; y = 0; z = -2.
; Ответ: x = 0; y = 0; z = -2.
