Свойства операции умножения матриц
Линейная алгебра
Основные определения
Определение. Матрицейразмера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А = 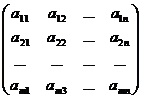
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij ± bij
С = А + В = В + А.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
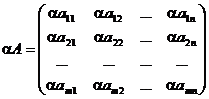
a (А+В) =aА ± aВ
А(a±b) = aА ± bА
Пример. Даны матрицы А = 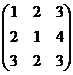 ; B =
; B = 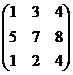 , найти 2А + В.
, найти 2А + В.
2А = 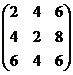 , 2А + В =
, 2А + В = 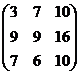 .
.
Операция умножения матриц
Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:
A×B = C;
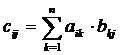 .
.
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Свойства операции умножения матриц
1)Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
А×Е = Е×А = А
Очевидно, что для любых матриц выполняются следующее свойство:
A×O = O; O×A = O,
где О – нулеваяматрица.
2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) Если произведение АВ определено, то для любого числа a верно соотношение:
a(AB) = (aA)B = A(aB).
5) Если определено произведение АВ , то определено произведение ВТАТ и выполняется равенство:
(АВ)Т = ВТАТ, где
индексом Т обозначается транспонированная матрица.
6) Заметим также, что для любых квадратных матриц det (AB) = detA×detB.
Пример. Найти произведение матриц А = 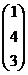 и В =
и В = 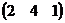 .
.
АВ = 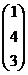 ×
× 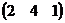 =
= 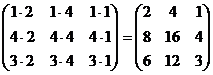 .
.
ВА = 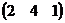 ×
× 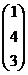 = 2×1 + 4×4 + 1×3 = 2 + 16 + 3 = 21.
= 2×1 + 4×4 + 1×3 = 2 + 16 + 3 = 21.
Пример. Найти произведение матриц А= 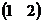 , В =
, В = 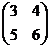
АВ = 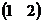 ×
× 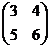 =
= 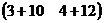 =
= 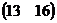 .
.
Определители (детерминанты)
Определение. Определителемквадратной матрицы А= 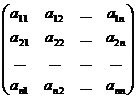 называется число, которое может быть вычислено по элементам матрицы по формуле:
называется число, которое может быть вычислено по элементам матрицы по формуле:
det A = 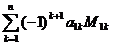 , где
, где
М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Предыдущая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:
det A = 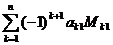
Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:
detA = 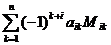 , i = 1,2,…,n.
, i = 1,2,…,n.
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1.
Для указанной матрицы А число М1к называется дополнительным минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
Определение. Дополнительный минор произвольного элемента квадратной матрицы aij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
Пример. Вычислить определитель матрицы А = 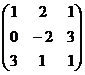
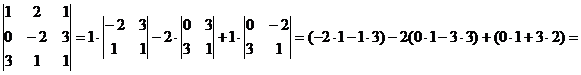
= -5 + 18 + 6 = 19.
Пример:. Даны матрицы А = 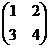 , В =
, В = 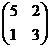 . Найти det (AB).
. Найти det (AB).
1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13;
det (AB) = det A ×det B = -26.
2- й способ: AB = 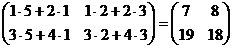 ,
,
det (AB) = 7×18 - 8×19 = 126 – 152 = -26.
Миноры
Определение. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется миноромматрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.
Заметим, что вышесказанное применимо не только к квадратным матрицам, но и к прямоугольным.
Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы будет являться дополнительным минором.
Алгебраические дополнения
Определение. Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы.
В частном случае, алгебраическим дополнением элемента матрицы называется его дополнительный минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.
Теорема Лапласа. Если выбрано s строк матрицы с номерами i1, … ,is, то определитель этой матрицы равен сумме произведений всех миноров, расположенных в выбранных строках на их алгебраические дополнения.
Обратная матрица
Определим операцию деления матриц как операцию, обратную умножению.
Определение.Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:
XA = AX = E,
где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратнойк матрице А и обозначается А-1.
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.
Рассмотрим общий подход к нахождению обратной матрицы.
Исходя из определения произведения матриц, можно записать:
AX = E Þ 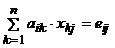 , i=(1,n), j=(1,n),
, i=(1,n), j=(1,n),
eij = 0, i ¹ j,
eij = 1, i = j .
Таким образом, получаем систему уравнений:
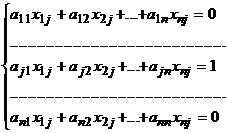 ,
,
Решив эту систему, находим элементы матрицы Х.
Пример. Дана матрица А = 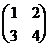 , найти А-1.
, найти А-1.
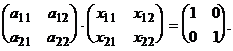
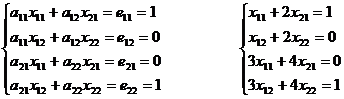
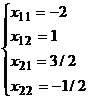
Таким образом, А-1= 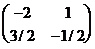 .
.
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:
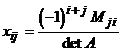 ,
,
где Мji- дополнительный минор элемента аji матрицы А.
Пример. Дана матрица А = 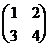 , найти А-1.
, найти А-1.
det A = 4 - 6 = -2.
M11=4; M12= 3; M21= 2; M22=1
x11= -2; x12= 1; x21= 3/2; x22= -1/2
Таким образом, А-1= 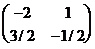 .
.
Пример. Дана матрица А = 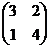 , найти А3.
, найти А3.
А2 = АА = 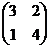
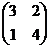 =
= 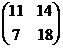 ; A3 =
; A3 = 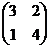
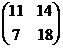 =
= 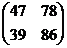 .
.
Отметим, что матрицы 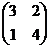 и
и 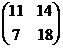 являются перестановочными.
являются перестановочными.
Пример. Вычислить определитель 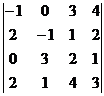 .
.
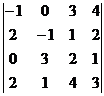 = -1
= -1 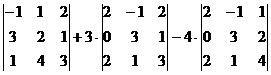
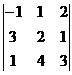 = -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.
= -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.
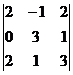 =
= 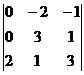 = 2(0 – 2) – 1(0 – 6) = 2.
= 2(0 – 2) – 1(0 – 6) = 2.
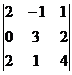 =
= 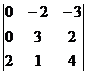 = 2(-4) – 3(-6) = -8 + 18 = 10.
= 2(-4) – 3(-6) = -8 + 18 = 10.
Значение определителя: -10 + 6 – 40 = -44.
Базисный минор матрицы
Ранг матрицы
Определение. В матрице порядка m´n минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n.
Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.
В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.
Определение. Порядок базисного минора матрицы называется рангомматрицы и обозначается Rg А.
Пример. Определить ранг матрицы.
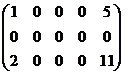 ~
~ 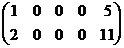 ~
~ 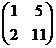 ,
, 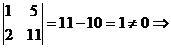 RgA = 2.
RgA = 2.
Пример: Определить ранг матрицы.
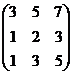 ~
~ 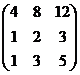 ~
~ 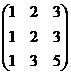 ~
~ 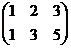 ,
, 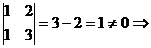 Rg = 2.
Rg = 2.
Пример. Определить ранг матрицы.
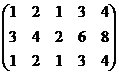 ~
~ 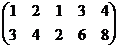 ,
, 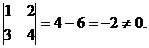 Þ Rg = 2.
Þ Rg = 2.
Метод Крамера
Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.
Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.
det A ¹ 0;
Действительно, если какое- либо уравнение системы есть линейная комбинация остальных, то если к элементам какой- либо строки прибавить элементы другой, умноженные на какое- либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
Теорема (Правило Крамера): Система из n уравнений с n неизвестными
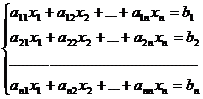
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di/D, где
D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di = 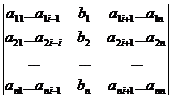
Пример.
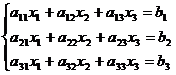
A = 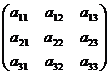 ; D1=
; D1= 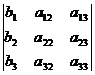 ; D2=
; D2= 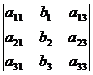 ; D3=
; D3= 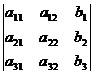 ;
;
x1 = D1/detA; x2 = D2/detA; x3 = D3/detA;
Пример. Найти решение системы уравнений:
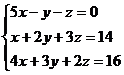
D = 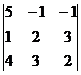 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 = 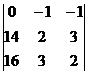 = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30.
x1 = D1/D = 1;
D2 = 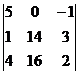 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
x2 = D2/D = 2;
D3 = 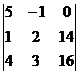 = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x3 = D3/D = 3.
Как видно, результат совпадает с результатом, полученным выше матричным методом.
Как было сказано выше, матричный метод и метод Крамера применимы только к тем системам линейных уравнений, в которых число неизвестных равняется числу уравнений. Далее рассмотрим произвольные системы линейных уравнений.
Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
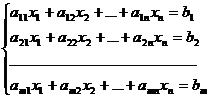 ,
,
где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.
Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.
Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.
Определение. Для системы линейных уравнений матрица
А = 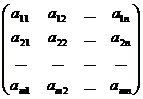 называется матрицей системы, а матрица
называется матрицей системы, а матрица
А*=  называется расширенной матрицей системы
называется расширенной матрицей системы
Определение. Если b1, b2, …,bm = 0, то система называется однородной. однородная система всегда совместна, т.к. всегда имеет нулевое решение.
Элементарные преобразования систем
К элементарным преобразованиям относятся:
1)Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.
2)Перестановка уравнений местами.
3)Удаление из системы уравнений, являющихся тождествами для всех х.
Теорема Кронекера – Капелли
(условие совместности системы)
Теорема:Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
RgA = RgA*.
Очевидно, что система (1) может быть записана в виде:
x1 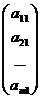 + x2
+ x2 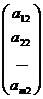 + … + xn
+ … + xn 
Пример. Определить совместность системы линейных уравнений:
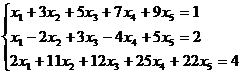
A = 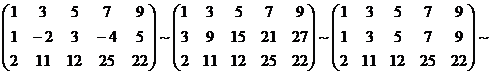
~ 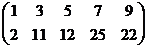 .
. 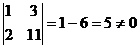 RgA = 2.
RgA = 2.
A* = 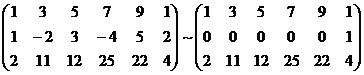 RgA* = 3.
RgA* = 3.
Система несовместна.
Пример. Определить совместность системы линейных уравнений.
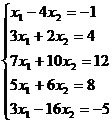 А =
А = 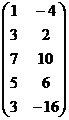 ;
; 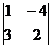 = 2 + 12 = 14 ¹ 0; RgA = 2;
= 2 + 12 = 14 ¹ 0; RgA = 2;
A* = 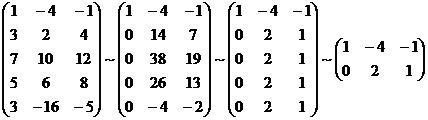
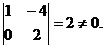 RgA* = 2.
RgA* = 2.
Система совместна. Решения: x1 = 1; x2 =1/2.
Метод Гаусса
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:
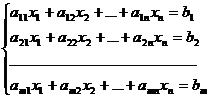
Разделим обе части 1–го уравнения на a11 ¹ 0, затем:
1) умножим на а21 и вычтем из второго уравнения
2) умножим на а31 и вычтем из третьего уравнения
и т.д.
Получим:
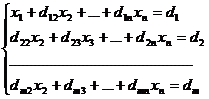 , где d1j = a1j/a11, j = 2, 3, …, n+1.
, где d1j = a1j/a11, j = 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
Пример. Решить систему линейных уравнений методом Гаусса.
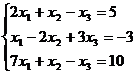
Составим расширенную матрицу системы.
А* = 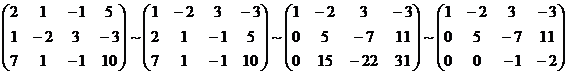
Таким образом, исходная система может быть представлена в виде:
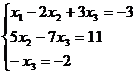 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.
Пример. Решить систему методом Гаусса.
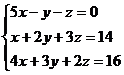
Составим расширенную матрицу системы.
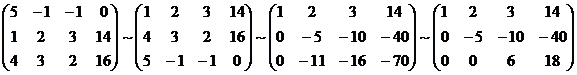
Таким образом, исходная система может быть представлена в виде:
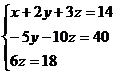 , откуда получаем: z = 3; y = 2; x = 1.
, откуда получаем: z = 3; y = 2; x = 1.
Полученный ответ совпадает с ответом, полученным для данной системы методом Крамера и матричным методом.
Элементы векторной алгебры
Определение. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.
Определение. Длиной (модулем) вектора называется расстояние между началом и концом вектора.
Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.
Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.
Определение. Линейными операциями над векторами называется сложение и умножение на число.
Суммой векторов является вектор - 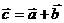
Произведение - 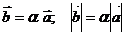 , при этом
, при этом  коллинеарен
коллинеарен  .
.
Вектор  сонаправлен с вектором
сонаправлен с вектором  (
( 
 ), если a > 0.
), если a > 0.
Вектор  противоположно направлен с вектором
противоположно направлен с вектором  (
(  ¯
¯  ), если a < 0.
), если a < 0.
Свойства векторов
1)  +
+  =
=  +
+  - коммутативность.
- коммутативность.
2)  + (
+ (  +
+ 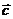 ) = (
) = (  +
+  )+
)+ 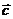
3)  +
+ 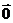 =
= 
4)  +(-1)
+(-1)  =
= 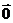
5) (a×b)  = a(b
= a(b  ) – ассоциативность
) – ассоциативность
6) (a+b)  = a
= a  + b
+ b  - дистрибутивность
- дистрибутивность
7) a(  +
+  ) = a
) = a  + a
+ a 
8) 1×  =
= 
Определение.
1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.
3)Базисом на прямой называется любой ненулевой вектор.
Определение. Если 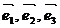 - базис в пространстве и
- базис в пространстве и 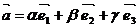 , то числа a, b и g - называются компонентами или координатами вектора
, то числа a, b и g - называются компонентами или координатами вектора  в этом базисе.
в этом базисе.
В связи с этим можно записать следующие свойства:
- равные векторы имеют одинаковые координаты,
- при умножении вектора на число его компоненты тоже умножаются на это число,
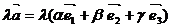 =
= 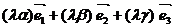 .
.
- при сложении векторов складываются их соответствующие компоненты.
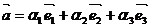 ;
; 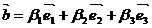 ;
;
 +
+  =
= 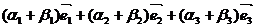 .
.
Система координат
Для определения положения произвольной точки могут использоваться различные системы координат. Положение произвольной точки в какой- либо системе координат должно однозначно определяться. Понятие системы координат представляет собой совокупность точки начала отсчета (начала координат) и некоторого базиса. Как на плоскости, так и в пространстве возможно задание самых разнообразных систем координат. Выбор системы координат зависит от характера поставленной геометрической, физической или технической задачи. Рассмотрим некоторые наиболее часто применяемые на практике системы координат.
Декартова система координат
Зафиксируем в пространстве точку О и рассмотрим произвольную точку М.
Вектор 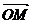 назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора.
назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора.
Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.
1-я ось – ось абсцисс
2-я ось – ось ординат
3-я ось – ось апликат
Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.
Если заданы точки А(x1, y1, z1), B(x2, y2, z2), то 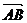 = (x2 – x1, y2 – y1, z2 – z1).
= (x2 – x1, y2 – y1, z2 – z1).
Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.
Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.
Пример. Даны векторы  (1; 2; 3),
(1; 2; 3),  (-1; 0; 3),
(-1; 0; 3), 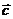 (2; 1; -1) и
(2; 1; -1) и 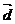 (3; 2; 2) в некотором базисе. Показать, что векторы
(3; 2; 2) в некотором базисе. Показать, что векторы  ,
,  и
и 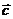 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 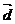 в этом базисе.
в этом базисе.
Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:
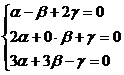 линейно независимы.
линейно независимы.
Тогда 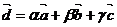 .
.
Это условие выполняется, если определитель матрицы системы отличен от нуля.
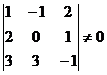
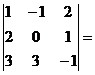
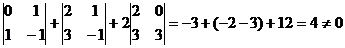
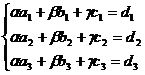
Для решения этой системы воспользуемся методом Крамера.
D1 = 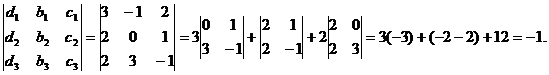
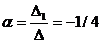 ;
;
D2 = 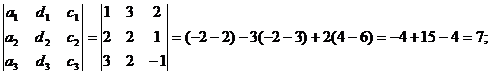
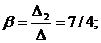
D3 = 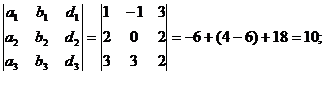
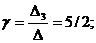
Итого, координаты вектора 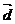 в базисе
в базисе  ,
,  ,
, 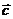 :
: 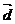 { -1/4, 7/4, 5/2}.
{ -1/4, 7/4, 5/2}.
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х1, y1, z1), B(x2, y2, z2), то 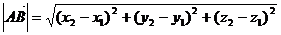 .
.
Если точка М(х, у, z) делит отрезок АВ в соотношении l/m, считая от А, то координаты этой точки определяются как:
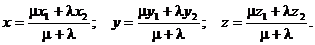
В частном случае координаты середины отрезка находятся как:
x = (x1 + x2)/2; y = (y1 + y2)/2; z = (z1 + z2)/2.
Общее уравнение плоскости
Определение. Плоскостьюназывается поверхность, все точки которой удовлетворяют общему уравнению:
Ax + By + Cz + D = 0,
где А, В, С – координаты вектора 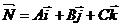 -вектор нормали к плоскости.
-вектор нормали к плоскости.
Возможны следующие частные случаи:
А = 0 – плоскость параллельна оси Ох
В = 0 – плоскость параллельна оси Оу
С = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
А = В = 0 – плоскость параллельна плоскости хОу
А = С = 0 – плоскость параллельна плоскости хОz
В = С = 0 – плоскость параллельна плоскости yOz
А = D = 0 – плоскость проходит через ось Ох
В = D = 0 – плоскость проходит через ось Оу
С = D = 0 – плоскость проходит через ось Oz
А = В = D = 0 – плоскость совпадает с плоскостью хОу
А = С = D = 0 – плоскость совпадает с плоскостью xOz
В = С = D = 0 – плоскость совпадает с плоскостью yOz
Коллинеарным плоскости
Пусть заданы два вектора 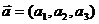 и
и 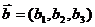 , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы
, коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы 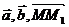 должны быть компланарны.
должны быть компланарны.
Уравнение плоскости:
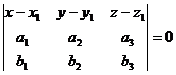
Полярная система координат
Определение. Точка О называется полюсом, а луч l – полярной осью.
Суть задания какой- либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол j называется полярным углом.
 |
М
r
r = 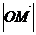
j
l
Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох.
Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями:
x = rcosj; y = rsinj; x2 + y2 = r2
Пример. Уравнение кривой в полярной системе координат имеет вид:
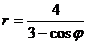 . Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.
. Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.
Воспользуемся связью декартовой прямоугольной и полярной системы координат: 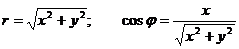 ;
;
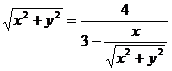
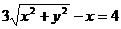
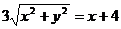
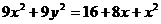
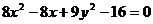
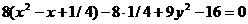
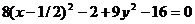
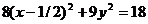
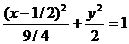
Получили каноническое уравнение эллипса. Из уравнения видно, что центр эллипса сдвинут вдоль оси Ох на 1/2 вправо, большая полуось a равна 3/2, меньшая полуось b равна 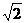 , половина расстояния между фокусами равно с =
, половина расстояния между фокусами равно с = 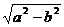 = 1/2. Эксцентриситет равен е = с/a = 1/3. Фокусы F1(0; 0) и F2(1; 0).
= 1/2. Эксцентриситет равен е = с/a = 1/3. Фокусы F1(0; 0) и F2(1; 0).
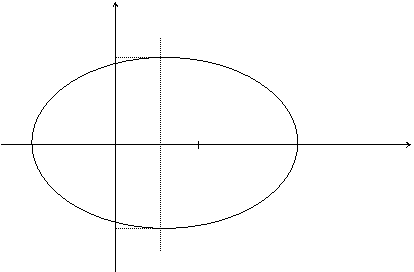
y
F1 F2
-1 0 ½ 1 2 x
- 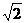
Пример. Уравнение кривой в полярной системе координат имеет вид:
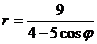 . Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.
. Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.
Подставим в заданное уравнение формулы, связывающие полярную и декартову прямоугольную системы координат.
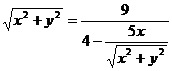
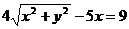
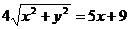
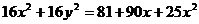
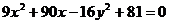
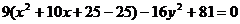
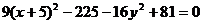
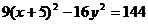
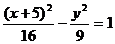
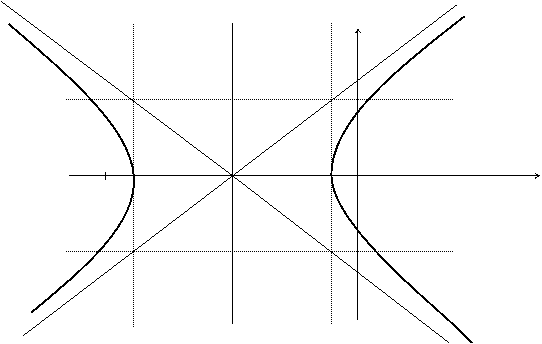
Получили каноническое уравнение гиперболы. Из уравнения видно, что гипербола сдвинута вдоль оси Ох на 5 влево, большая полуось а равна 4, меньшая полуось b равна 3, откуда получаем c2 = a2 + b2 ; c = 5; e = c/a = 5/4.
Фокусы F1(-10; 0), F2(0; 0).
Построим график этой гиперболы.
 |
y
F1 -9 -5 -1 0 F2 x
-3
Предел функции в точке
 y f(x)
y f(x)
A + e
A
A - e
0 a - D a a + D x
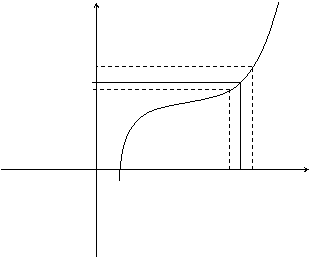
Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)
Определение. Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х таких, что
0 < ïx - aï < D
верно неравенство ïf(x) - Aï< e.
То же определение может быть записано в другом виде:
Если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.
Запись предела функции в точке: 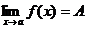
Основные теоремы о пределах
Теорема 1. 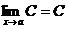 , где С = const.
, где С = const.
Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.
Теорема 2. 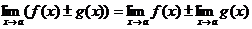
Доказательство этой теоремы будет приведено ниже.
Теорема 3. 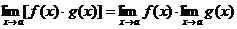
Следствие. 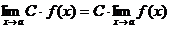
Теорема 4. 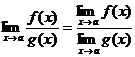 при
при 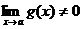
Теорема 5. Если f(x)>0 вблизи точки х = а и 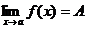 , то А>0.
, то А>0.
Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.
Теорема 6. Если g(x) £ f(x) £ u(x) вблизи точки х = а и 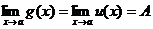 , то и
, то и 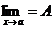 .
.
Пример. Найти предел 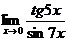
Так как tg5x ~ 5x и sin7x ~ 7x при х ® 0, то, заменив функции эквивалентными бесконечно малыми, получим:
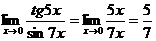
Пример. Найти предел
