Матричный способ решения систем линейных уравнений

Пусть дана система из n линейных уравнений с n неизвестными (т.е. ее основная матрица A – квадратная):

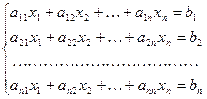(3.1)

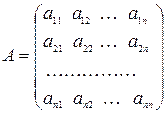
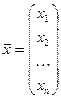
Обозначая 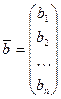, получаем, что система (3.1) равносильна одному матричному уравнению

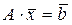(3.2)

Пусть $A^-1. Тогда

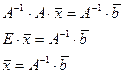
Получили теорему.

Теорема. Если основная матрица A системы линейных уравнений квадратная и существует обратная к ней матрица A^-1, то вектор-столбец решений получается домножением матрицы A^-1 слева на столбец свободных членов.

Пример.

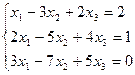
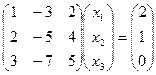
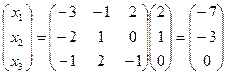Þ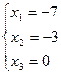

(обратная матрица к A взята из предыдущего примера).

Упражнения

23. Найти все решения матричного уравнения:

a) ;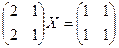

b) .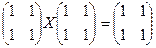

24. Умножить матрицы:

a) ;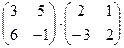

b) ;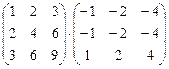

c) ;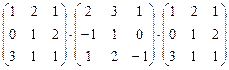

d) ;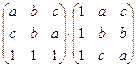

e) .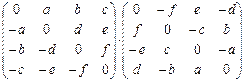

25. Выполнить действия:

a) ;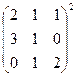

b) ;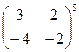

c) ;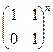

d) .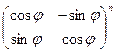

26. Найти 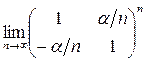, α - вещественное число.

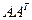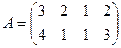27. Вычислить , где , а 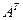- матрица, транспонированная к A.

28. Доказать, что:

a) ;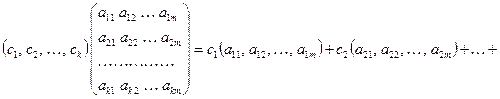

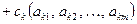b) .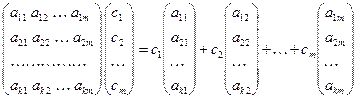

29. Решить системы линейных уравнений матричным способом

a) ;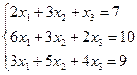

b) ;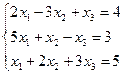

c) ;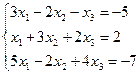

d) ;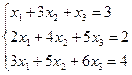

e) .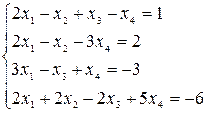

Глава 4. Определители

Слово детерминант происходит от латинского determino – «ограничивать», «определять» и его буквальный смысл – «определитель». Термин встречается впервые у Гаусса и означает при этом дискриминант квадратичной формы (1801 г). В современном значении этот термин ввел Коши (1815 г). Идея детерминанта восходит к Лейбницу, который пришел к детерминантам при решении систем линейных уравнений, рукопись относится к 1678 году. Первые полные изложения теории определителей принадлежат Бине и Коши.

Определители 2-го, 3-го порядков

Рассмотрим систему:

(*)

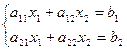Домножим каждую из строк матрицы вначале на 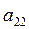и 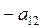, а затем на 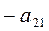и 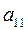соответственно, и сложим строки:

+

.

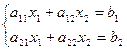
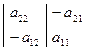
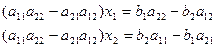Определение. Определителем квадратной матрицы второго порядка 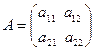будем называть выражение вида:

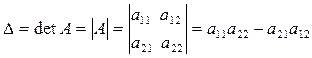. (1)

Обозначая:

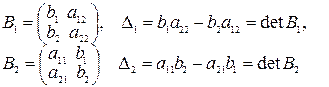
получаем .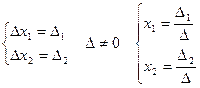

Рассмотрим систему:

(**)

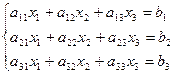Определение. Определителем квадратной матрицы A третьего порядка будем называть выражение вида:

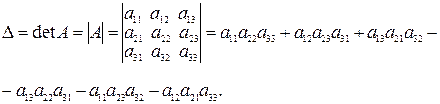(2)

Обозначая 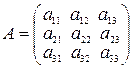, , 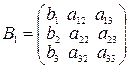, 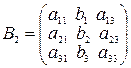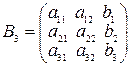и производя несложные преобразования, можно убедиться, что, если D=detA≠0, то решение системы (**) вычисляется по формулам:

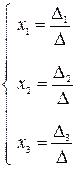, где D_k=detB_k, k=1, 2, 3.

Рассмотренные случаи приводят нас к общему понятию определителя.

Определители n-го порядка

Определение. Перестановкой из n чисел 1, 2, 3,…, n будем называть всякое расположение этих чисел, записанное в определенном порядке. Множество всех перестановок из n чисел обозначается .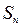

Например, S₃={(123), (132), (213), (231), (312), (321)}.

Число перестановок в 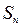: n!=1·2·3·…·n.

Будем говорить, что два числа в перестановке составляют инверсию (беспорядок), если большее из них расположено левее меньшего.

Определение. Перестановку a= 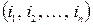будем называть четной, если общее число инверсий I 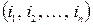в ней четное, и нечетной, если общее число инверсий – нечетное.

Пример.

Перестановка из 9 чисел a=(3, 8, 4, 1, 7, 9, 6, 2, 5) является четной, поскольку общее число инверсий в ней I(a)=2+6+2+0+3+3+2+0+0=18.

Теорема. Если переставить местами 2 произвольных элемента i_k и i_k+l в перестановке a= 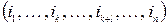, полученная перестановка b= 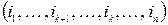будет другой четности.

Доказательство.

Если переставляются местами два соседних элемента i_k и i_k+1, то утверждение теоремы очевидно, поскольку b сохраняет все инверсии перестановки a, кроме инверсии, образованной (или не образованной) самими элементами i_k и i_k+1. В общем случае поменять местами элементы i_k и i_k+l можно, совершив l+(l-1)=2l+1 перестановок двух соседних элементов (i_k«i_k+1, i_k+1«i_k+2,..., i_k+1-1«i_k+1,
i_k+1-1«i_k+1-2,..., i_k+1«i_k), т.е. нечетное число раз поменяв четность всей перестановки a. В итоге получается перестановка b другой четности. Теорема доказана.

Рассмотрим квадратную матрицу порядка n:

.

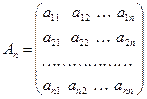Определение. Определителем квадратной матрицы 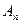n-го порядка называется алгебраическая сумма n! слагаемых, состоящих из n сомножителей - элементов матрицы 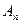, выбранных по одному из каждой строки и каждого столбца. При этом, если номера строк элементов, входящих в произведение, записаны в порядке возрастания, а номера их столбцов образуют перестановку a, то данное произведение берется со знаком «+», если перестановка a четная, и со знаком «-», если она – нечетная. Обозначается определитель матрицы A так: detA или |A|.

.

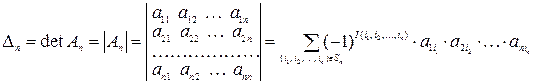Замечание. Применяя данное определение к матрицам 2-го и 3-го порядков, получаем уже выведенные ранее формулы (1) и (2).

Свойства определителей

1. Если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю.

Доказательство.

Данное свойство непосредственно следует из определения определителя, поскольку каждое участвующее в нем слагаемое в качестве множителя будет содержать 0.

2. Если строки матрицы поменять местами, то определитель новой матрицы и определитель исходной матрицы будут различаться знаками.

Доказательство.

Рассмотрим 2 матрицы A и B, где B получена из A перестановкой s-ой и t-ой строк, s<t:

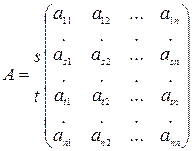и .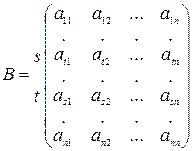

Тогда

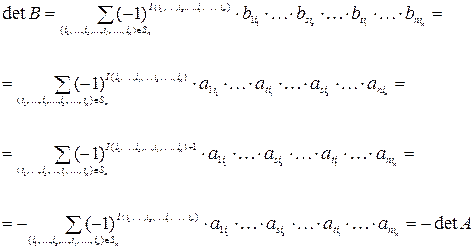
(воспользовались предыдущей теоремой об изменении четности перестановки при перестановке двух ее членов). Свойство доказано.

3. Если матрица содержит две одинаковые (пропорциональные) строки, то определитель этой матрицы равен нулю.

Доказательство.

Если в матрице A s-я и t-я строки совпадают, переставляя их местами и пользуясь предыдущим свойством, получаем: detA=-detA, откуда detA=0.

4. Если матрица B получается из матрицы A умножением произвольной строки на некоторое число l, то определитель B получается из определителя A умножением на то же число:
detB=ldetA.

Доказательство.

Рассмотрим 2 матрицы A и B, где B получена из A умножением s-ой строки на число l:

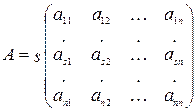и .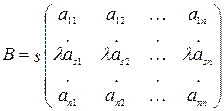

Тогда

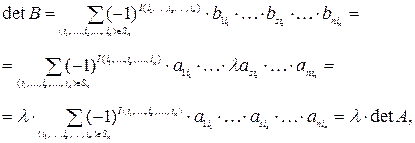
что и требовалось доказать.

5. Если в матрице A некоторая строка получается как сумма двух строк (т.е. каждый элемент этой строки представляет из себя сумму двух элементов), то определитель A раскладывается в сумму двух определителей, у которых в данной строке осталось одно слагаемое, а все остальные строки совпадают с соответствующими строками матрицы A.

Доказательство.

Рассмотрим 3 матрицы A, A' и A'', все строки которых, кроме s-ой, совпадают, а s-я строка A получена сложением s-ых строк матриц A' и A'':

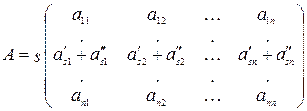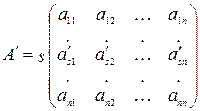, и .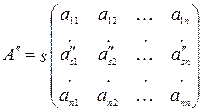

Тогда

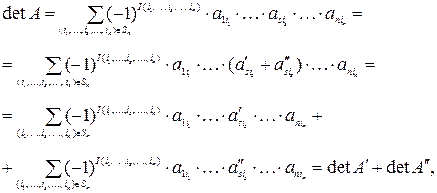
что и требовалось доказать.

6. Если какая-либо строка матрицы является линейной комбинацией остальных строк, то определитель этой матрицы равен 0.

Доказательство.

Получается последовательным применением свойств 5, 4 и 3.

Следствия:

1. 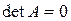Û A - особенная матрица.

2. .

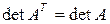3. Значение 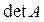не изменится, если:

а) к какой-либо строке прибавить другую строку;

б) к какой-либо строке прибавить линейную комбинацию остальных строк.

4. Определитель произведения матриц равен произведению их определителей.