Системы линейных уравнений. Матричный способ решения СЛУ. Формулы Крамера. Метод Гаусса

Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные^[2]. Пусть исходная система выглядит следующим образом

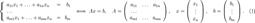
Матрица A называется основной матрицей системы, b — столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

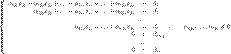
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных ^[3].

Тогда переменные называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число , где i > r, то рассматриваемая система несовместна.

Пусть для любых i > r.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом 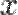( , где 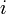— номер строки):

,
где

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевымопределителем

основной матрицы (причём для таких уравнений решение существует и единственно). Создан Габриэлем Крамером в 1751 году.^{[источник не указан 387 дней]}

Описание метода

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

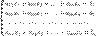
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

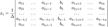
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

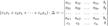
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,...,b_n и x₁,x₂,...,x_n, либо набор c₁,c₂,...,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

[