Модели принятия решений. Принятие решений при различных уровнях неопределенности ситуации

Модель принятия (выбора) решений (МВР) описывает систему управления на прагматическом уровне. МВР состоит из следующих пяти элементов:

· стратегий – S – множества возможных вариантов решений;

· состояний объективных условий – R – множества возможных состояний внешней среды, в которых нужно принимать решения;

· прогноза наступления состояний объективных условий – P – вероятностей наступления состояний объективных условий;

· результатов – L – наборов характеристик системы, являющихся следствием выбора конкретной стратегии и наступления конкретных внешних условий, L_ij=L(s_i,r_j);

· критерия эффективности (оптимальности, целесообразности) – F(S,R,P,L).

Состояния среды Стратегии	r1	r2	. . .	rm
s1	L11	L12	. . .	L1m
s2	L21	L22	. . .	L2m
. . .	. . .
sn	Ln1	Ln2	. . .	Lnm
Вероятности	p1	p2	. . .	pm

В реальных, имеющих практическое значение ситуациях, формирование стратегии, как и выявление возможного состояния условий, требует выполнения определенной работы, может быть длительной и трудоемкой. Причем в процессе отбора стратегий и внешних условий они рассматриваются, уточняются, совершенствуются и поэтому естественно считать, что непосредственно в МВР число их ограничено.

В рамках общей МВР возможны разные варианты полноты информации о состоянии объективных условий.

1.Если возможно только одно состояние объективных условий r₁, которому соответствует прогноз p₁=1, то говорят, что решение принимается в условиях достоверности (полной определенности). Оптимальной является стратегия, при которой достигается 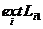. Если результат желательно увеличить (например, L_ij – объем выпуска, качество продукции и т. п.), то критерий принятия решения имеет вид 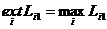. Если результат желательно уменьшить (например, L_ij – затраты, брак, время работы и т. п.), то критерий принятия решения имеет вид 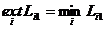. В задаче линейного программирования состояние объективных условий включает: число переменных, число ограничений, матрицу коэффициентов ограничений, вектор правых частей ограничений, вектор коэффициентов целевой функции.

2.Если возможны два и более состояний внешней среды и вероятность их возникновения установлена, то имеет место выбор решения в условиях риска (статистической определенности). В качестве критерия принятия решения используется критерий Байеса-Лапласа – максимум или минимум среднего результата: .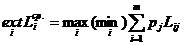

3.Прогнозирование часто затруднительно, а результаты прогнозирования на длительный период имеют сомнительную ценность. Если сделать достоверный прогноз невозможно, т. е. известен лишь перечень возможных состояний внешней среды, а вероятности их возникновения неизвестны, то вся информация о ситуации заключена в матрице результатов. В этом случае говорят о принятии решения в условиях неопределенности. Наиболее часто в качестве критериев принятия решения в условиях неопределенности применяются критерии «недостаточного основания», Вальда, Сэвиджа, Гурвича.

Критерий «недостаточного основания» является частным случаем критерия Байеса-Лапласа. Из отсутствия оснований считать, что какое-то состояние объективных условий вероятнее других, делается предположение, что все состояния равновероятны, т. е. 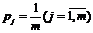. Такой прогноз позволяет свести задачу к выбору решения в условиях риска, с критерием .

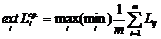Критерий Вальда (минимаксный или максиминный критерий). Суть данного критерия состоит в обеспечении получения самого хорошего результата при самых неблагоприятных условиях, то есть это критерий гарантированного результата. Для каждой стратегии находится наихудший из возможных результатов и выбирается такая стратегия, которая приводит к наилучшему из наихудших результатов. Для «затрат» критерий имеет вид: 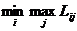, а для «результатов»: .

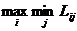Критерий Сэвиджа (критерий минимума сожалений) обеспечивает сведение к минимуму возможных сожалений (потерь от упущенных возможностей), под которыми понимается разность между результатами оптимальной и текущей стратегии при реализовавшихся объективных условиях. Рассчитав сожаления для всех возможных объективных условий и стратегий, составляют матрицу сожалений или последствий ошибочных решений. Критерий имеет вид: 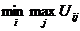, где U_ij – потери (сожаления) от упущенных возможностей при выборе стратегии s_i и наступлении объективных условий r_j. U_ij=|L_j-L_ij|, , .

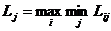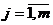Критерий Гурвича рекомендует при выборе стратегии рассчитывать на осуществление промежуточного между наилучшими и наихудшими для данной стратегии состояниями объективных условий:

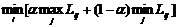для «затрат»,

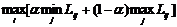для «результатов»,

a - коэффициент пессимизма.