Раскрытие неопределенности. Правило Лопиталя

Теорема 3.6. (теорема Лопиталя, раскрытие неопределенности вида ).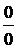

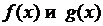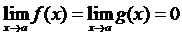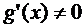Пусть функции определены и дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a. Пусть, далее и в указанной окрестности точки a. Тогда, если существует предел отношения производных 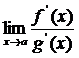(конечный или бесконечный), то существует и предел 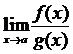, причем справедлива формула

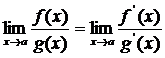(3.14)

Эту теорему обычно называют правилом Лопиталя.

Замечание 1. Если производные 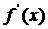и 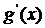удовлетворяют тем же требованиям, что и сами функции 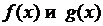, то правило Лопиталя можно применить повторно. При этом получаем

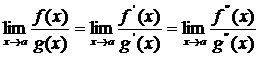
Замечание 2.Теорема остается верной и в случае, когда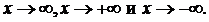

Примеры.Вычислить пределы. Разделим производную числителя на производную знаменателя

1.

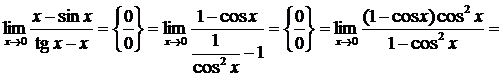
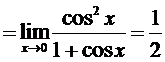
2.

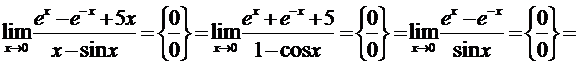
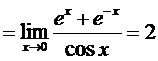
Замечание 3.Если в формулировке теоремы заменить требование 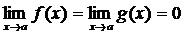на условие , то теорема остается справедливой, то есть можем раскрывать неопределенность вида .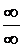

Пример

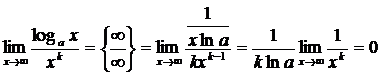
Вывод: степенная функция 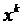- бесконечно большая более высокого порядка, чем логарифмическая функция .

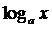Раскрытие других видов неопределенностей

Неопределенности вида 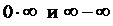можно свести к неопределенностям 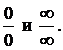Покажем это на примерах. Вычислим следующие пределы, преобразовав на первом шаге исходную функцию:

1.

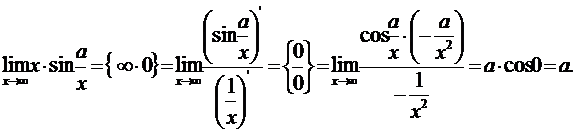
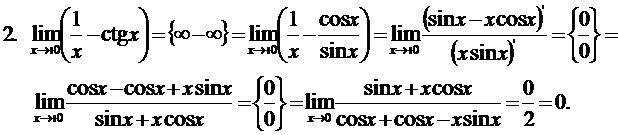
Неопределенности вида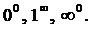

Примеры.Вычислить пределы.

1.

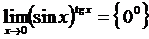
Но 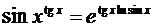и в показателе степени получена неопределенность вида 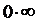, получаем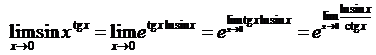

Рассмотрим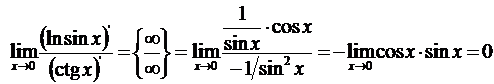

окончательно получаем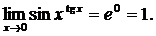

2.

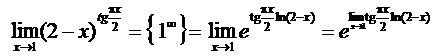
Рассмотрим

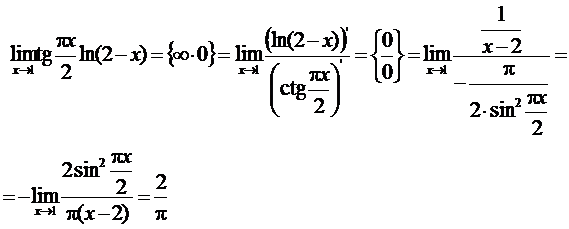
окончательно получаем

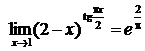
Формула Тейлора

Формула Тейлора – одна из главных формул математического анализа, позволяющая функцию, заданную сложным для вычисления аналитическим выражением, заменить удобным для анализа многочленом.

Теорема 3.7.(Тейлора)

Пусть функция 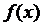имеет в точке a и некоторой ее окрестности производные порядка n+1. Пусть x – любое значение аргумента из указанной окрестности,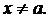

Тогда между точками a и x найдется точка c такая, что справедлива следующая формула:

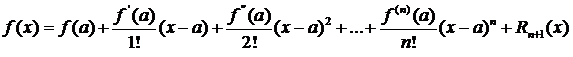(3.15)

Эта формула называется формулой Тейлора, а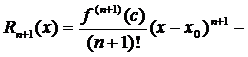

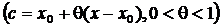
остаточный член, записанный в форме Лагранжа.

Эту формулу можно записать в виде 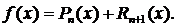Таким образом, формула Тейлора дает возможность заменить функцию 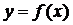многочленом 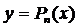с соответствующей степенью точности, равной значению остаточного члена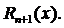

Формула Маклорена

При a=0 получаем частный случай формулы Тейлора – формулу Маклорена.

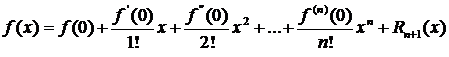(3.16)

Остаточный член в форме Лагранжа имеет вид: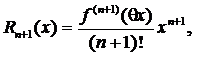

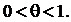
Разложение некоторых

Элементарных функций по формуле Маклорена

1.

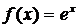
Так как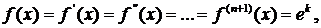

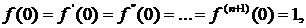
то формула Маклорена имеет вид:

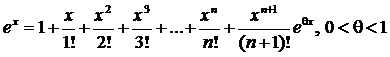
2.

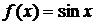
Так как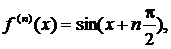

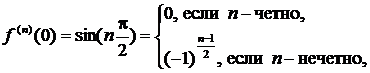
то формула Маклорена имеет вид

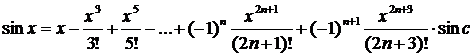
3.

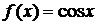
Так как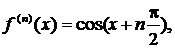

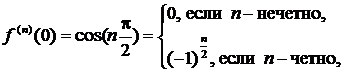
то формула Маклорена имеет вид:

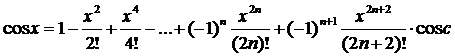
4. Аналогично можно получить:

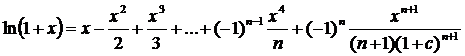
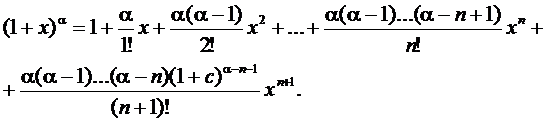
Пример

Сколько членов в формуле Маклорена требуется взять для того, чтобы вычислить значение e с точностью 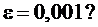(найти n).

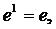тогда по формуле Маклорена имеем (x=1):

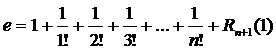
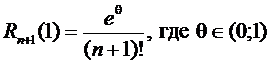
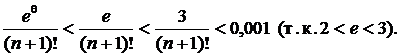
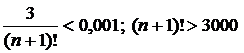
для n=2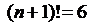

для n=3

для n=4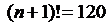

для n=5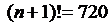

для n=6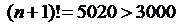

Следовательно, если взять n=6, то требуемое неравенство удоволетворяется.