Линейные операции над векторами. Разложение векторов.
2.1.1. В треугольнике АВС дано: 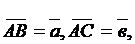 точка М- середина стороны ВС. Выразить вектор
точка М- середина стороны ВС. Выразить вектор 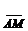 через векторы
через векторы 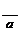 и
и 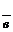 .
.
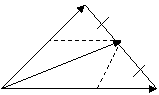
Решение: Через точку М проведем прямые, параллельные сторонам АВ и АС. Получим параллелограмм 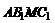 (рис. 1), в котором АМ является диагональю. Следовательно,
(рис. 1), в котором АМ является диагональю. Следовательно, 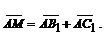 Но
Но 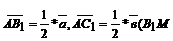 и
и 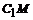 - средние линии, поэтому
- средние линии, поэтому 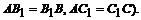 Получаем
Получаем 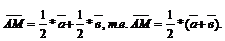
 |
В
М
А С
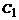
рис. 1.
2.1.2. Какому условию должны удовлетворять не нулевые векторы



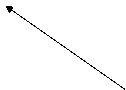

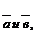 чтобы имело место соот- А D
чтобы имело место соот- А D
ношение 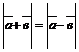 ?
? 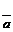
 Решение: Построим на векторах
Решение: Построим на векторах 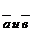 , О В
, О В
отложенных от точки О, параллелог- 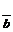
рамм ОАDB (рис. 2). Тогда рис.2.
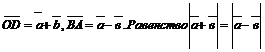
означает, что длины диагоналей параллелограмма равны, т.е. 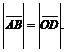 Отсюда следует, что данный параллелограмм есть прямоугольник. Следовательно, векторы
Отсюда следует, что данный параллелограмм есть прямоугольник. Следовательно, векторы 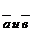 перпендикулярны.
перпендикулярны.
2.1.3. По данным векторам 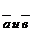 построить векторы:
построить векторы:
1) 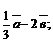 2)
2) 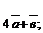
3) 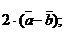
4) 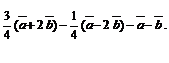
2.1.4. Даны векторы 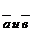 . Коллинеарны ли векторы
. Коллинеарны ли векторы 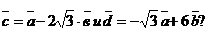
2.1.5. При каких значениях λ векторы 2λ· 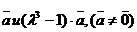 имеют одинаковое направление?
имеют одинаковое направление?
2.1.6.При каких значениях х векторы 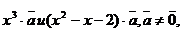 противоположно направлены?
противоположно направлены?
2.1.7.Дано: 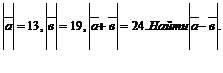
2.1.8.Дано: 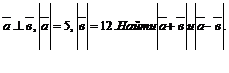

2.1.9.В треугольнике АВС: М – точка пересечения медиан треугольника, 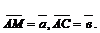 Разложить
Разложить 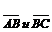 по векторам
по векторам 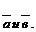
2.1.10. В параллелограмме АВСД: К и М – середины сторон ВС и СД. 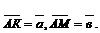 Выразить векторы
Выразить векторы 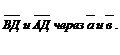
2.1.11. Точка О является центром тяжести (точка пересечения медиан) треугольника АВС. Доказать, что 
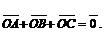
2.1.12. В четырехугольнике АВСД диагонали, пересекаясь, делятся пополам. Доказать, что этот четырехугольник – параллелограмм.
2.1.13. Даны две точки А1(3;-4;1) и А2(4;6;-3). Найти координаты вектора 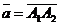 .
.
2.1.14. Даны три последовательные вершины параллелограмма: А(1;-2;3), В(3;2;1), С(6;4;4). Найти его четвертую вершину D.
2.1.15. Найти координаты вектора 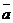 , если известно, что он направлен в противоположную сторону к вектору
, если известно, что он направлен в противоположную сторону к вектору 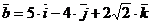 , и его модуль равен 5.
, и его модуль равен 5.
2.1.16. Вектор 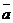 составляет с осями Ох и Оу углы α=600 и β=1200. Найти его координаты, если
составляет с осями Ох и Оу углы α=600 и β=1200. Найти его координаты, если 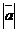 =2.
=2.
2.1.17. Разложить вектор 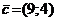 по векторам
по векторам 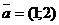 и
и 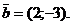
Решение: Требуется представить вектор 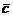 в виде
в виде 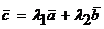 , где
, где 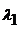 и
и 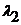 – числа. Найдем их, используя определение равенства векторов. Имеем:
– числа. Найдем их, используя определение равенства векторов. Имеем: 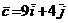 ,
, 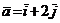 ,
, 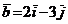 и равенство
и равенство 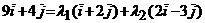 , т.е.
, т.е. 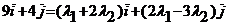 . Отсюда следует
. Отсюда следует
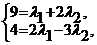
т.е. 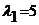 ,
, 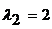 .Следовательно,
.Следовательно, 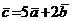 .
.
2.1.18. Доказать, что в любом треугольнике длины его сторон пропорциональны синусам противолежащих углов (теорема синусов).
Решение: Рассмотрим треугольник АВС. Пусть 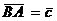 ,
, 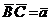 ,
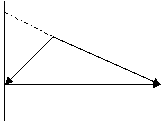
, 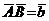 . В плоскости треугольника АВС возьмем вспомогательную ось l, перпендикулярную, например, вектору
. В плоскости треугольника АВС возьмем вспомогательную ось l, перпендикулярную, например, вектору 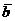 и спроектируем на эту ось векторы
и спроектируем на эту ось векторы 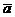 ,
, 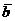 и
и 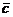 (рис.3). Так как
(рис.3). Так как 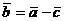 , то
, то 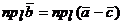 , т.е.
, т.е. 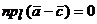 ,
, 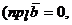 т.к.
т.к. 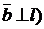 . Поэтому
. Поэтому 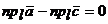 , т.е.
, т.е. 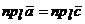 .
.
 Но
Но 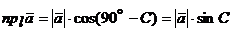 , а
, а 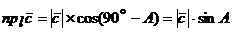 . Поэтому
. Поэтому 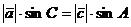 или
или
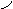
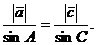

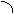
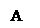 Выбрав ось перпендикулярную, например, вектору
Выбрав ось перпендикулярную, например, вектору 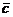 , аналогично получим:
, аналогично получим:

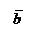
|
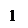
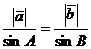
Из двух последних равенств следует, что
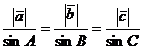 .
.
2.1.19. Найти координаты вектора 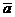 , если
, если 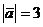 и углы между вектором и координатными осями равны
и углы между вектором и координатными осями равны 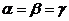 .
.
2.1.20. Луч образует с двумя осями координат углы в 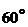 . Под каким углом наклонен он к третьей оси?
. Под каким углом наклонен он к третьей оси?
2.1.21. Даны векторы 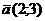 ,
, 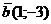 ,
, 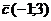 . При каком значении коэффициента
. При каком значении коэффициента 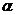 векторы
векторы 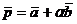 и
и 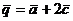 коллинеарны?
коллинеарны?
2.1.22. Даны точки A(-1;5;-10), B(5;-7;8), C(2;2;-7), D(5;-4;2). Проверить что векторы 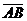 и
и 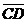 коллиниарны; установить, какой из них длиннее и во сколько раз; направлены они в одну сторону или в разные?
коллиниарны; установить, какой из них длиннее и во сколько раз; направлены они в одну сторону или в разные?
2.1.23. Представить вектор 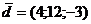 как линейную комбинацию векторов
как линейную комбинацию векторов 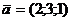 ,
, 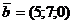 и
и 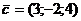 .
.
2.1.24. На оси Oy найти точку М, равноудаленную от точек А(1;-4;7) и В(5;6;-5).
2.1.25. На оси Ox найти точку М, расстояние которой от точки А(3;-3) равно 5.
2.1.26. Даны вершины треугольника А(3;-1;5), В(4;2;-5), С(-4;0;3). Найти длину медианы, проведенной из вершины А.
Разное.
2.1.27. Дано разложение вектора 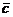 по базису
по базису 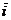 ,
, 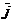 ,
, 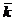 :
: 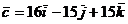 . Найти разложение по этому же базису вектора
. Найти разложение по этому же базису вектора 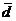 , параллельного вектору
, параллельного вектору 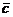 и противоположного с ним направления, при условии, что
и противоположного с ним направления, при условии, что 
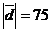 .
.
2.1.28. Пусть векторы 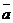 и
и 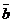 неколлинеарны и
неколлинеарны и 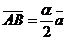 ,
, 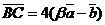 ,
, 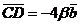 ,
, 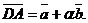 Найти α и β и доказать коллинеарность векторов
Найти α и β и доказать коллинеарность векторов 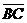 и
и 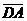 .
.
2.1.29. Даны четыре точки А, В, С, D. Точки M и N- середины отрезков AC и BD. Доказать, что 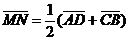 .
.
2.2. Скалярное произведение.
2.2.1. Дано: 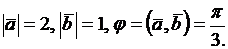 Найти модуль вектора
Найти модуль вектора 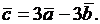
2.2.2. Дано: 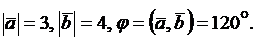 Найти модуль вектора
Найти модуль вектора 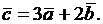
2.2.3. Выразить длины медиан произвольного треугольника через длины его сторон.
Решение:
Рассмотрим треугольник АВС. Пусть AD – одна из медиан




 В
В
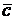 D
D
А 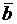 С
С
рис.4
треугольника (рис. 4). Введем в рассмотрение векторы 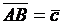 ,
, 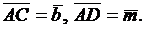
Тогда 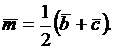 Возведем обе части равенства в квадрат:
Возведем обе части равенства в квадрат: 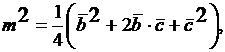 т. е.
т. е. 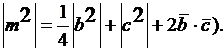
А так как 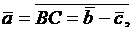 то
то 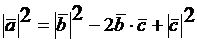 . Значит
. Значит 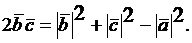 В итоге получаем
В итоге получаем 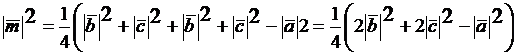 и далее
и далее 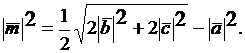
2.2.4. Проверить, могут ли векторы 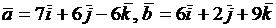 быть ребрами куба. Найти третье ребро куба.
быть ребрами куба. Найти третье ребро куба.
Решение: Векторы 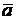 и
и 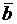 можно принять за ребра куба, если они ортогональны и имеют равные длины. Проверим это:
можно принять за ребра куба, если они ортогональны и имеют равные длины. Проверим это: 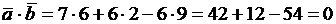 , значит
, значит 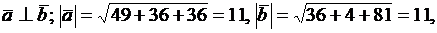 значит
значит 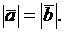
Найдем третье ребро 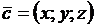 куба. Так как
куба. Так как 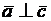 , то
, то 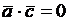 , т. е.
, т. е. 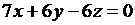 ; так как
; так как 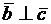 , то
, то 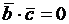 , т. е.
, т. е. 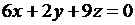 ; из равенства
; из равенства 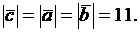 Для нахождения координат вектора
Для нахождения координат вектора 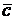 решим систему уравнений
решим систему уравнений
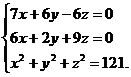
Из первых двух уравнений выражаем 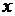 и
и 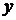 через
через 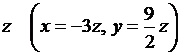 и подставляем их значения в третье уравнение системы:
и подставляем их значения в третье уравнение системы: 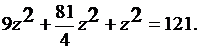 Отсюда находим, что
Отсюда находим, что 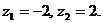 Тогда
Тогда 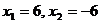 и
и 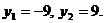 Таким образом,
Таким образом, 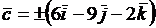 .
.
2.2.5. Найти угол между диагоналями параллелограмма, построенного на векторах 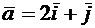 и
и 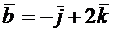 .
.
2.2.6. Найти вектор 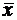 , зная, что
, зная, что 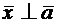 ,
, 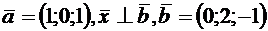 , проекция вектора
, проекция вектора 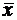 на вектор
на вектор 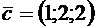 равна 1.
равна 1.
2.2.7. Даны вершины треугольника 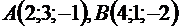 и
и 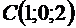 .
.
Найти:
а) внутренний угол при вершине С;
б) 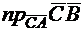 .
.
Решение:
а) Угол 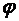 при вершине С есть угол между векторами
при вершине С есть угол между векторами 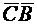 и
и 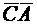 . Определим координаты этих векторов:
. Определим координаты этих векторов:
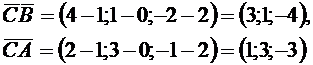
Найдем их модули:
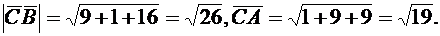
Найдем cos 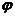 :
:
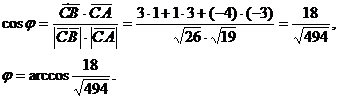
б) 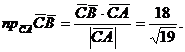
2.2.8. Даны векторы 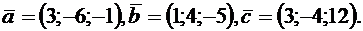 Найти
Найти 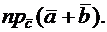
2.2.9. Даны некомпланарные векторы 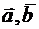 и
и 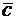 , причём
, причём 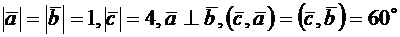 . Найти
. Найти
а) 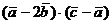 ;
;
б) 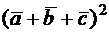 .
.
2.2.10. Даны векторы 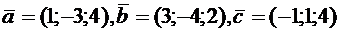 . Найти
. Найти 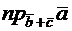 .
.
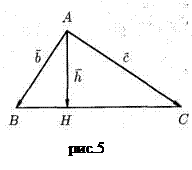
2.2.11. В треугольнике АВС: 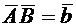 ,
, 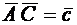 . Выразить вектор
. Выразить вектор 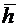 , направленный по высоте АН, через векторы
, направленный по высоте АН, через векторы 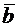 и
и 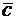 .
.
Решение: Имеем (рис.5): 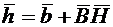 . Но
. Но 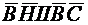 , где
, где 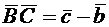 . Поэтому
. Поэтому
| |
| |
| |
| |
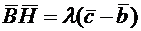 и
и 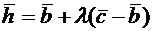 . Множитель
. Множитель 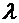 найдем из условия
найдем из условия 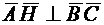 . Значит
. Значит 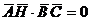 , т.е
, т.е 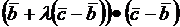 =0. Получаем
=0. Получаем 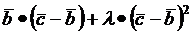 =0; откуда находим
=0; откуда находим 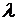 =
= 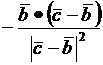 . Найденное значение
. Найденное значение 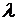 подставляем в выражение для вектора
подставляем в выражение для вектора 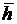 :
: 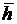 =
= 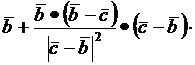
 |
2.2.12. Единичные векторы 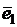 ,
, 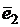 ,
, 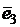 удовлетворяют условию
удовлетворяют условию
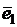 +
+ 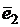 +
+ 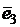 =
= 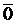 . Найти
. Найти 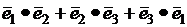 .
.
2.2.13. Дано: 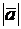 =3,
=3, 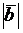 =2,
=2, 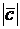 =5,
=5, 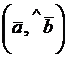 =
= 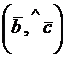 =
= 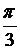 , векторы
, векторы 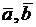 и
и
2.2.14. 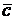 - компланарны. Найти модуль вектора
- компланарны. Найти модуль вектора 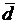 =
= 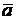 +
+ 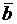 -
- 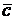 .
.
Найти вектор 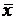 , зная, что он перпендикулярен к оси Оz и удовлетворяет условиям
, зная, что он перпендикулярен к оси Оz и удовлетворяет условиям 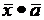 =9,
=9, 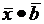 = -4, где
= -4, где 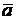 =(3;-1;5),
=(3;-1;5), 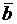 =(1;2;-3).
=(1;2;-3).
Разное.
2.2.15. Показать, что четырехугольник с вершинами А(-5;3;4),
В(-1;-7;5), С(6;-5;-3) и D(2;5;-4) есть квадрат.
2.2.16. Доказать, что 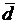 =
= 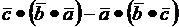 перпендикулярен
перпендикулярен
вектору 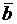 .
.
2.2.17. Найти вектор 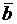 , коллинеарный вектору
, коллинеарный вектору 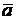 =
= 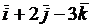 и удовлетворяющий
и удовлетворяющий
условию 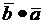 =28.
=28.
2.2.18. Дано: 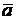 =
= 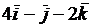 ,
, 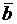 =(2;1;2). Найти:
=(2;1;2). Найти:
a) 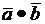 ;
;
б) 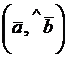 ;
;
в) 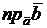 ;
;
г) 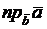 .
.
2.2.19. Какую работу производит сила 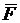 =(2;-1;-4), когда точка ее приложения,
=(2;-1;-4), когда точка ее приложения,
двигаясь прямолинейно, перемещается из точки А(1;-2;3) в точку В(5;-6;1).
2.2.20. Найти работу равнодействующей сил 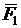 =
= 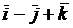 и
и 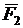 =
= 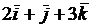
при перемещении ее точки приложения из начала координат в точку
М(2;-1;-1).
2.2.21. При каком значении 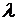 векторы
векторы 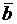 =
= 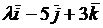 и
и 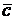 =
= 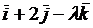
взаимно перпендикулярны?
2.2.22. В треугольнике АВС вершины имеют координаты А(1;1;-1), В(2;3;1),
С(3;2;1). Найти:
а) длины сторон;
б) внутренние углы;
в) острый угол между медианой BD и стороной АС.
2.2.23. Найти углы между осями координат и радиус-вектором точки М(-2;3;1).
