Необходимый признак сходимости ряда.
Достаточные признаки сходимости рядов с положительными членами.
1. Необходимый признак сходимости ряда.
Ряд 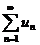 может сходиться только при условии, что его общий член un при неограниченном увеличении номера n стремится к нулю :
может сходиться только при условии, что его общий член un при неограниченном увеличении номера n стремится к нулю : 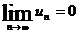 ,
,
Если 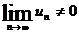 , то ряд
, то ряд 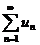 расходится – это достаточный признак расходимости ряда.
расходится – это достаточный признак расходимости ряда.
. Достаточные признаки сходимости ряда с положительными членами.
а) Признак сравнения рядов с положительными членами.
Исследуемый ряд сходится, если его члены не превосходят соответствующих членов другого, заведомо сходящегося ряда: исследуемый ряд расходится, если его члены превосходят соответствующие члены другого заведомо расходящегося ряда. При исследовании рядов на сходимость и расходимость по этому признаку часто используется геометрический ряд
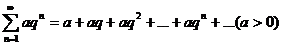 ,
,
Который сходится при 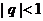 и расходится при
и расходится при 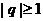 , и гармонический ряд
, и гармонический ряд
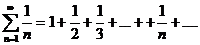
Являющийся расходящимся.
При исследовании рядов используется также обобщенный гармонический ряд
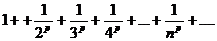
Если p=1, то данный ряд обращается в гармонический ряд, который является расходящимся.
Если p<1, то члены данного ряда больше соответствующих членов гармонического ряда и, значит, он расходится. При p>1 имеем геометрический ряд, в котором 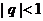 : он является сходящимся. Итак, обобщённый гармонический ряд сходится при p>1 и расходится при
: он является сходящимся. Итак, обобщённый гармонический ряд сходится при p>1 и расходится при 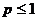 .
.
Признак сходимости Лейбница для знакочередующихся рядов. Если члены знакочередующегося ряда монотонно убывают по абсолютной величине и общий член un стремится к нулю при 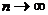 , то ряд сходится.
, то ряд сходится.
Этот признак служит достаточным признаком сходимости знакочередующихся рядов.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд
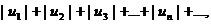
Составленный из абсолютных величин его членов, т.е. всякий абсолютно сходящийся ряд является сходящимся.
Если знакопеременный ряд сходится, а составленный из абсолютных величин его членов ряд расходится, то данный ряд называется условно (неабсолютно) сходящимся. Заметим, что из расходимости ряда в общем случае не следует расходимость ряда.
Для установления абсолютной сходимости знакопеременного (и знакочередующегося) ряда используются те же признаки, что и для сходимости ряда с положительными членами.
Для решения вопроса об абсолютной или условной сходимости знакочередующегося ряда необходимо рассмотреть ряд, составленный из абсолютных величин членов знакочередующегося ряда.
Если при исследовании этого ряда с помощью одного из признаков сходимости (признака Даламбера, признака сравнения рядов) ряд окажется сходящимся, то данный знакочередующийся ряд сходится абсолютно; если же ряд окажется расходящимся, то знакочередующийся ряд сходится условно.
Примеры решения упражнений.
Пример 1.
Вычислите пределы фукций: 1) 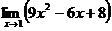 ; 2)
; 2) 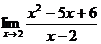 ; 3)
; 3) 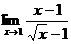 .
.
Решение.
1) 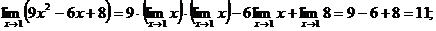
2) Поскольку предел знаменателя равен 0, то воспользоваться теоремой о пределе частного невозможно. Поэтому первоначально сократим дробь, разложив числитель на множители:
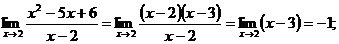
3)
| |
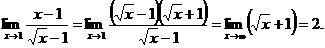
Ответ. 1) 11, 2) –1, 3) 2.
Пример 2.
Найдем производные следующих функций:
1) 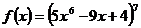 ;
;
2) 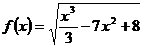 ;
;
3) 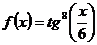 .
.
Решение.
1) Полагаем, что 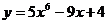 , тогда
, тогда 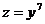 . Отсюда, согласно формуле для расчета производной сложной функции, имеем:
. Отсюда, согласно формуле для расчета производной сложной функции, имеем:
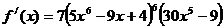 .
.
2) Полагаем, что 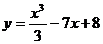 , тогда
, тогда 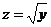 . Отсюда, согласно формуле для расчета производной сложной функции, имеем:
. Отсюда, согласно формуле для расчета производной сложной функции, имеем:
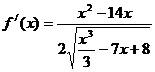 .
.
3) Имеем, что
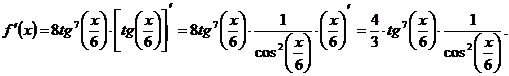
Пример 3.
Исследуем функцию и построим эскиз ее графика:
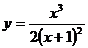
Решение.
1. Определим область существования этой функции. Функция существует при всех значениях х, кроме 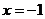 , при котором знаменатель дроби обращается в нуль. Значит, функция определена в интервалах (—
, при котором знаменатель дроби обращается в нуль. Значит, функция определена в интервалах (— 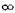 , —1)
, —1) 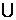 (—1, +
(—1, + 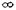 ).
).
2. Исследуем вопрос о наличии центра симметрии к оси симметрии. Проверим для этого, выполняются ли равенства 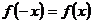 или
или 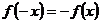 .
.
Непосредственная подстановка убеждает нас, что ни одно из этих равенств не выполняется, так что ни центра, ни оси симметрии график функции не имеет.
3. Определяем точки разрыва. Числитель и знаменатель дробно-рациональной функции 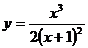 представляют собой непрерывные функции и, следовательно, функция у будет непрерывной при всех значениях х, кроме
представляют собой непрерывные функции и, следовательно, функция у будет непрерывной при всех значениях х, кроме 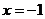 , при котором знаменатель дроби обращается в нуль.
, при котором знаменатель дроби обращается в нуль.
4. Переходим к определению асимптот графика.
а) Вертикальные асимптоты найдем, приравняв знаменатель нулю:
2(х+1)2 = 0; отсюда 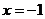 .
.
Вертикальная асимптота одна: ее уравнение 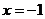 .
.
б) Горизонтальные асимптоты находим так: отыскиваем
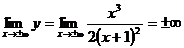 ,
,
а это означает, что горизонтальных асимптот нет.
в) Наклонные асимптоты:
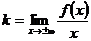
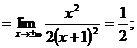
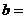
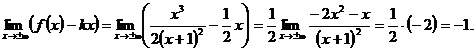
Наклонная асимптота одна: 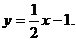
5 и 6. Определяем интервалы возрастания и убывания функции и экстремум функции.
Находим первую производную: 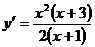 . Определим критические точки:
. Определим критические точки:
1) Решаем уравнение 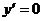 , т. е. уравнение
, т. е. уравнение 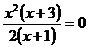 и находим, что
и находим, что 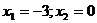 .
.
2) Определяем значения х, при которых 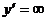 . Таким значением является
. Таким значением является 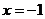 Но это значение не должно подлежать рассмотрению, так как оно не входит в область определения функции. Критические точки, подлежащие рассмотрению:
Но это значение не должно подлежать рассмотрению, так как оно не входит в область определения функции. Критические точки, подлежащие рассмотрению: 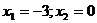 и точка
и точка 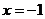 – разделяют область существования функции на такие интервалы:
– разделяют область существования функции на такие интервалы: 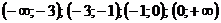 .
.
В каждом из этих интервалов производная сохраняет знак: в первом — плюс, во втором — минус, в третьем — плюс, в четвертом — плюс (в этом можно убедиться, взяв в каждом интервале произвольное значение х и вычислив при нем значение у'). Последовательность знаков первой производной запишется так: +, —, +, +. Значит, в интервале 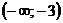 функция возрастает, в интервале
функция возрастает, в интервале 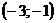 – убывает, в интервалах
– убывает, в интервалах 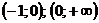 функция возрастает.
функция возрастает.
При 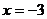 функция имеет максимум и
функция имеет максимум и 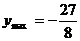 . Так как знаки во втором и третьем интервалах различны, то можно было бы предположить, что при
. Так как знаки во втором и третьем интервалах различны, то можно было бы предположить, что при 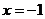 есть экстремум. Но такое предположение неверно, так как при
есть экстремум. Но такое предположение неверно, так как при 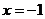 заданная функция не существует. Итак, функция имеет единственный экстремум (максимум) при
заданная функция не существует. Итак, функция имеет единственный экстремум (максимум) при 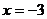 .
.
7. Определяем интервалы выпуклости и вогнутости графика функции и точек перегиба.
Находим, что 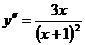 и определяем критические точки второго рода:
и определяем критические точки второго рода:
1) решаем уравнение 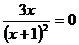 и находим, что
и находим, что 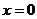 ;
;
2) определяем значения х, при котором 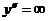 . Таким значением является
. Таким значением является 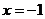 . Как уже было отмечено выше, это значение рассматриваться не должно, так как при нем не существует заданной функции.
. Как уже было отмечено выше, это значение рассматриваться не должно, так как при нем не существует заданной функции.
Критическая точка второго рода 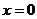 разделяет интервалы (—
разделяет интервалы (— 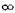 , —1) и (—1, +
, —1) и (—1, + 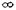 ). существования функции на интервалы:
). существования функции на интервалы: 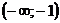 ,
, 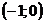 и
и 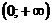 .
.
В каждом из этих интервалов вторая производная конечна и сохраняет знак: в первом – минус, во втором – минус, в третьем – плюс, и мы имеем такое чередование знаков второй производной в этих интервалах: —, —, +.
Значит, в интервалах 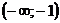 и
и 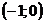 кривая выпукла, а в интервале
кривая выпукла, а в интервале
(0, + ∞) — вогнута. При 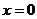 вторая производная равна нулю, а при переходе из второго интервала в третий она поменяла знак. Это указывает на то, что при
вторая производная равна нулю, а при переходе из второго интервала в третий она поменяла знак. Это указывает на то, что при 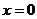 , кривая имеет точку перегиба. Координаты точки перегиба (0, 0) — это начало координат.
, кривая имеет точку перегиба. Координаты точки перегиба (0, 0) — это начало координат.
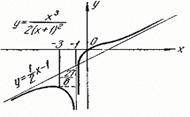 Рис. 9 Рис. 9 | 8. Определение точек пересечения графика с осями координат и исследование промежутков монотонности произведите самостоятельно. График функции пересекает оси координат в единственной точке 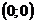 . Функция отрицательна на промежутках . Функция отрицательна на промежутках 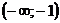 и и 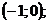 положительна на промежутке положительна на промежутке 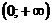 . . |
Все полученные сведения наносим на чертеж и получаем эскиз кривой (см. рис. 9).
Пример 4.
Найдем 1) 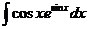 , 2)
, 2) 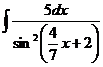
Решение.
1)
|
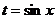 . Тогда
. Тогда 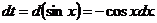
Произведя подстановку, получим:
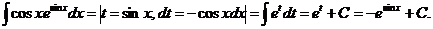
2) Так как аргумент подынтегральной функции имеет вид 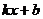 , где
, где 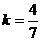 , то, применяя вышеназванную теорему, получим:
, то, применяя вышеназванную теорему, получим:
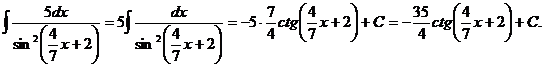
Пример 5.
Вычислим 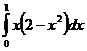 .
.
Решение.
Положим 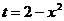 . Тогда
. Тогда 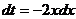 . Вычислим значения новых пределов интегрирования, подставив в формулу новой переменной исходные значения пределов:
. Вычислим значения новых пределов интегрирования, подставив в формулу новой переменной исходные значения пределов: 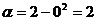 ,
, 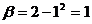 . Воспользовавшись формулой замены переменной в определенном интеграле, получим:
. Воспользовавшись формулой замены переменной в определенном интеграле, получим:
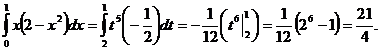
Пример 6.
Исследовать сходимость ряда, используя признак Даламбера:
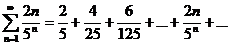
Решение. Подставив в общий член ряда 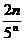 вместо n число n+1, получим
вместо n число n+1, получим 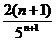 . Найдём предел отношения (n+1)-ого члена к n-му члену при
. Найдём предел отношения (n+1)-ого члена к n-му члену при 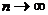 :
:
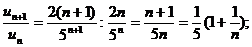
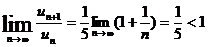 .
.
Следовательно, данный ряд сходится.
Пример 7.
Формула простых процентов:
P - первоначальная сумма кредита
через один год: P+ 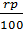 = p (1+
= p (1+ 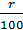 )
)
через два года: P (1+ 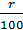 ) +
) + 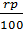 = p (1+
= p (1+ 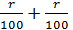 ) = p(1+
) = p(1+ 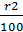 )
)
через три года: P(1+ 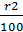 ) +
) + 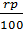 = p(1+
= p(1+ 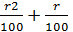 ) = p (1+
) = p (1+ 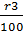 )
)
через n лет: P (1+ 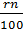 )
)
S = P (1+ 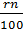 )
)
Формула сложных процентов:
P - первоначальная сумма кредита
через один год: 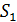 = P+
= P+ 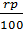 = p (1+
= p (1+ 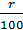 )
)
через два года: 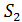 = P(1+
= P(1+ 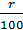 ) + p (1+
) + p (1+ 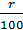 )
) 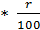 = p (1+
= p (1+ 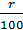 ) (1+
) (1+ 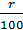 ) = p (1+
) = p (1+ 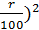
через три года: p (1+ 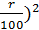 + p (1+
+ p (1+ 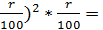 p (1+
p (1+ 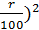 (1+
(1+ 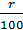 ) = p (1+
) = p (1+ 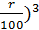
через n лет: p (1+ 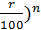
S = p (1+ 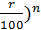
Задача.
Какие условия получения кредита в размере 100 денежных единиц на 3 года выгоднее: под 20% годовых на основе сложного процента или под 15% годовых на основе простого процента с выплатой один раз по окончании срока?
Sсл = 100(1+ 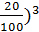 = 100 ·
= 100 · 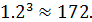 8
8
Sпр = 100(1+ 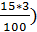 = 100 ·
= 100 · 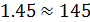
Задания для контрольной работы
Для получения аттестации по учебной дисциплине «Математика» необходимо выполнить домашнюю контрольную работу, сдать экзамен.
Разделы, изучаемые в учебной дисциплине «Математика»
1. Математический анализ
2. Основы теории комплексных чисел
3. Основы теории вероятностей
4. Основные численные методы
5. Задача на проценты
Методические указания для выполнения ДКР:
· ДКР состоит из 7 заданий. Количество вариантов 10.
· Номер варианта выбирается по двум последним цифрам студенческого билета.
· Текст практических заданий необходимо переписать.
· Обязательно написание всех формул с последующей расшифровкой букв и символов.
· Работа выполняется в тетради вручную или в печатном варианте. Отдельные листы необходимо скрепить.
· На проверку ДКР сдается не позднее двух недель до начала сессии. В случае возврата преподавателем выполненной ДКР, ошибки исправляются в этой же тетради, первый отзыв должен быть приложен к работе.
Контрольная работа засчитывается, если соблюдены все требования и все задания выполнены верно.
Желаем Вам успехов в самостоятельном изучении материала
и решении предложенных задач!
Задания для ДКР
Вариант 1
1) Вычислите предел функции: 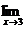
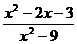
2) Найдите производную функции при данном значении аргумента: f(x) = 2sin2x; f/( 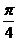 )
)
3) Найдите экстремумы функции: y = 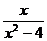
4) Найдите неопределенный интеграл: 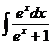
5) Вычислите: 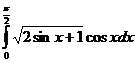 .
.
6) Используя признак Даламбера, исследовать на сходимость ряд: 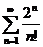
7) Какие условия приобретения депозитного сертификата в размере 200 ден.ед. на 3 года выгоднее: под 25% годовых на основе простого процента с выплатой один раз по окончании срока и или под 20% годовых на основе сложного процента?
Вариант 2
1) Вычислите предел функции: 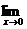
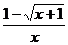
2) Найдите производную функции при данном значении аргумента: f(x) = 3cos2x; f/(- 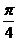 )
)
3) Найдите экстремумы функции: y = 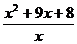
4) Найдите неопределенный интеграл: 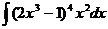
5) Вычислите: 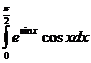 .
.
6) Используя признак Даламбера, исследовать на сходимость ряд: 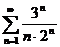
7) Сколько необходимо лет, чтобы получить 720 ден.ед., вложив 180 ден.ед. при ставке сложного процента 60% годовых, начисляемых ежегодно? Ежеквартально?
Вариант 3
1) Вычислите предел функции: 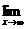
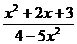
2) Найдите производную функции при данном значении аргумента: f(x) = ln(cosx); f/( 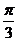 )
)
3) Найдите экстремумы функции: y = 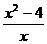
4) Найдите неопределенный интеграл: 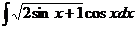
5) Вычислите: 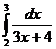
6) Используя признак Даламбера, исследовать на сходимость ряд: 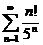
7) Сколько средств надо вложить на основе сложного процента под 20% годовых, начисляемых ежеквартально, чтобы получить через год 400 ден.ед.? А в случае начисления простых процентов?
Вариант 4
1) Вычислите предел функции: 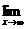 (1+
(1+ 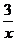 )x
)x
2) Найдите производную функции при данном значении аргумента: f(x) = ln(sinx); f/( 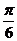 )
)
3) Найдите экстремумы функции: y = 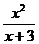
4) Найдите неопределенный интеграл: 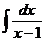
5) Вычислите: 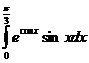
6) Используя признак Даламбера, исследовать на сходимость ряд: 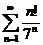
7) Какие условия приобретения депозитного сертификата в размере 200 ден.ед. на 3 года выгоднее: под 25% годовых на основе простого процента с выплатой один раз по окончании срока и или под 20% годовых на основе сложного процента?
Вариант 5
1) Вычислите предел функции: 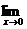
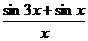
2) Найдите производную функции при данном значении аргумента: f(x) = 4cos2x); f/( 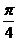 )
)
3) Найдите экстремумы функции: y = 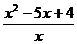
4) Найдите неопределенный интеграл: 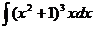 .
.
5) Вычислите: 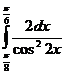
6) Используя признак Даламбера, исследовать на сходимость ряд: 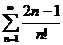
7) Какие условия приобретения депозитного сертификата в размере 200 ден.ед. на 3 года выгоднее: под 25% годовых на основе простого процента с выплатой один раз по окончании срока и или под 20% годовых на основе сложного процента?
Вариант 6
1) Вычислите предел функции: 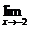
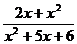
2) Найдите производную функции при данном значении аргумента: f(x) = ln 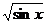 ; f/(
; f/( 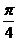 )
)
3) Найдите экстремумы функции: y = 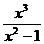
4) Найдите неопределенный интеграл: 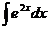 .
.
5) Вычислите: 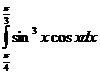
6) Используя признак Даламбера, исследовать на сходимость ряд: 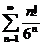
7) Сколько необходимо лет, чтобы получить 720 ден.ед., вложив 180 ден.ед. при ставке сложного процента 60% годовых, начисляемых ежегодно? Ежеквартально?
Вариант 7
1) Вычислите предел функции: 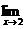
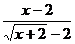
2) Найдите производную функции при данном значении аргумента: f(x) = arctg 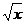 ; f/(
; f/( 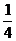 )
)
3) Найдите экстремумы функции: y = 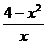
4) Найдите неопределенный интеграл: 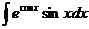
5) Вычислите: 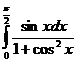 .
.
6) Используя признак Даламбера, исследовать на сходимость ряд: 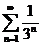
7) Сколько средств надо вложить на основе сложного процента под 20% годовых, начисляемых ежеквартально, чтобы получить 400 ден.ед.? А в случае начисления простых процентов.
Вариант 8
1) Вычислите предел функции: 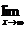
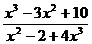
2) Найдите производную функции при данном значении аргумента: f(x) = e 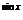 ; f/(0)
; f/(0)
3) Найдите экстремумы функции: y = 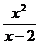
4) Найдите неопределенный интеграл: 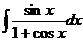
5) Вычислите: 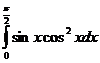
6) Используя признак Даламбера, исследовать на сходимость ряд: 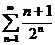
7) Какие условия приобретения депозитного сертификата в размере 200 ден.ед. на 3 года выгоднее: под 25% годовых на основе простого процента с выплатой один раз по окончании срока и или под 20% годовых на основе сложного процента?
Вариант 9
1) Вычислите предел функции: 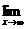 (1-
(1- 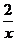 )x
)x
2) Найдите производную функции при данном значении аргумента: f(x) = e 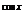 ; f/(
; f/( 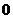 )
)
3) Найдите экстремумы функции: y = 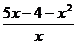
4) Найдите неопределенный интеграл: 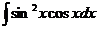
5) Вычислите: 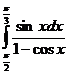
6) Используя признак Даламбера, исследовать на сходимость ряд: 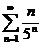
7) Какие условия приобретения депозитного сертификата в размере 200 ден.ед. на 3 года выгоднее: под 25% годовых на основе простого процента с выплатой один раз по окончании срока и или под 20% годовых на основе сложного процента?
Вариант 10
1) Вычислите предел функции: 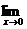
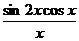 .
.
2) Найдите производную функции при данном значении аргумента: f(x) = cos2x2; f/( 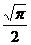 )
)
3) Найдите экстремумы функции: y = 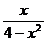
4) Найдите неопределенный интеграл: 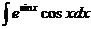
5) Вычислите: 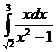
6) Используя признак Даламбера, исследовать на сходимость ряд: 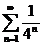
7) Сколько средств надо вложить на основе сложного процента под 20% годовых, начисляемых ежеквартально, чтобы получить 400 ден.ед.? А в случае начисления простых процентов?
3. Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
Основные источники:
1. Богомолов Н.Б. Практические занятия по математике: учебное пособие для студентов средних специальных учебных заведений. Высш. шк., 2007
2. Богомолов Н.Б., П.И.Самойленко Математика: учебник для студентов образовательных учреждений среднего профессионального образования. Дрофа, 2006
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие 2007.
4. Гмурман В.Е. Теория вероятностей и математическая статистика.
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в
упражнениях и задачах (в двух частях), 2006г.
6. Лапчук М.П, М.И.Рагулина, Е.К.Хеннер Численные методы: учебное пособие Издательский центр «Академия», 2007
7. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие для студентов образовательных учреждений среднего профессионального образования. – Ростов н/Д: Феникс, 2007
8. Спирина М.С., Спирин П.А. Дискретная математика: учебник для студентов образовательных учреждений среднего профессионального образования. Издательский центр «Академия», 2007.
Дополнительные источники:
1. Вентцель. Е.С. Теория вероятностей образования учебник для студентов высших учебных заведений. Издательский центр «Академия», 2005
2. Григорьев В.П., Ю.А.Дубинский Элементы высшей математики: учебник для студентов образовательных учреждений среднего профессионального образования. Издательский центр «Академия», 2004
3. Саакян С.М., А.М.Гольдман, Д.В.Денисов Задачи по алгебре и началам анализа: пособие для учащихся 10 – 11 кл. Просвещение, 2005
4. Шипачев С.М. Начала высшей математики: пособие для вузов. Дрофа, 2002
Интернет-ресурсы:
1. http://en.edu/ru – естественнонаучный портал;
2. http://schools.techno.ru – сайт «Школы в Интернете»
3. http://www.school.edu.ru – российский образовательный портал
4.http://www.alleng.ru- сайт «Образовательные ресурсы Интернета школьникам и студентам и др.
