Исследование функции при помощи дифференциального исчисления

Общая схема исследования функции и построения ее графика.

1. Найти область определения функции.

2. Исследовать функцию на четность – нечетность.

3. Исследовать вид разрыва в точках разрыва (если они есть).

4. Найти вертикальные асимптоты. (Для этого определяются значения левосторонних и правосторонних пределов в точках разрыва и выясняется, конечные они или бесконечные. Если пределы бесконечны, то прямая х = х₀ – вертикальная асимптота).

5. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты (для этого определяются пределы функции на бесконечности. Если 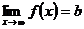, то у = b – горизонтальная асимптота. Если 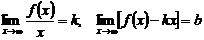, то прямая 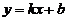является наклонной асимптотой графика функции).

6. Найти экстремумы и промежутки монотонности функции:

- найти производную функции,

- найти критические точки функции, в которых производная равна нулю или не существует,

- исследовать знаки производной слева и справа от каждой критической точки и сделать вывод о характере монотонности и наличии экстремумов функции (если производная на некотором интервале принимает положительные значения, то функция на этом интервале возрастает; если производная отрицательна, то функция убывает; если при переходе через критическую точку производная функции меняет свой знак с минуса на плюс, то данная точка является точкой минимума; если при переходе через критическую точку производная функции меняет свой знак с плюса на минус, то данная точка является точкой максимума).

7.Найти интервалы выпуклости функции и точки перегиба:

- найти вторую производную функции ,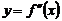

- найти точки, в которых вторая производная равна нулю или не существует,

- исследовать знаки второй производной слева и справа от каждой из найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба функции (если вторая производная функции на некотором интервале положительна, то функция выпукла вниз на этом интервале; если вторая производная функции на некотором интервале отрицательна, то функция выпукла вверх на этом интервале; если вторая производная при переходе через некоторую точку меняет свой знак, то эта точка является точкой перегиба).

- найти значения функций в точках перегиба.

8. Найти точки пересечения с осями координат, промежутки знакопостоянства и, возможно, некоторые дополнительные точки, уточняющие график.

Схема может варьироваться (например, для тригонометрических функций вводится исследование на периодичность), ее «шаги» могут меняться местами, однако их смысл при этом не меняется.

Первообразная функции. Неопределенный интеграл и его свойства.

Таблица интегралов.

Функция F(x) называется первообразной функцией для функции f(x) на промежутке Х, если в каждой точке х этого промежутка .

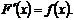Свойство первообразной.

Если F₁(x) и F₂(x) – первообразные для функции f(x) в некотором промежутке Х, то найдется такое число С, что справедливо равенство: .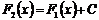

Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x) и обозначается .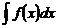

Согласно определению, .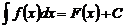

Свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции: .
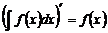2. Дифференциал неопределенного интеграла равен подынтегральному выражению: .
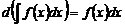3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого: .
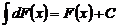4. Постоянный множитель можно выносить за знак интеграла: .
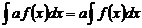5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:
6. .

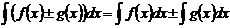Таблица интегралов:

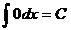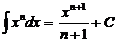; (при п ¹ –1); ;

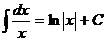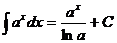(при а > 0, a ¹ 0);

; ; ;

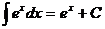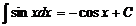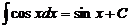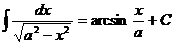(при );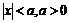

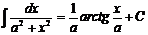(при a ¹ 0);

;

;

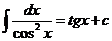
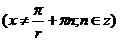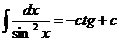
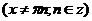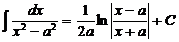(при a ¹ 0); .

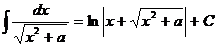Определенный интеграл

Пусть предел интегральной суммы при стремлении 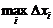к нулю существует, конечен и не зависит от способа выбора точек х₁, х₂,… и точек x₁, x₂,… Тогда этот предел называется определенным интегралом от функции у=f(x) на [a; b], обозначается 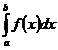, а сама функция у = f(x) называется интегрируемой на [a; b], т.е.

.

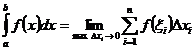Свойства определенного интеграла:

1. Постоянный множитель можно выносить за знак интеграла:

.

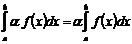2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций: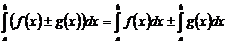

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е.

.

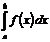
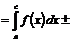
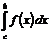4. Если на отрезке [a; b] f(x) £ g(x), то и £ .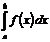

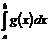5. Если функция у = f(x) непрерывна на отрезке [a; b], то найдется такое значение x Î [a; b], что .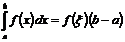

Формула Ньютона-Лейбница.

Пусть функция у = f(x) непрерывна на отрезке [a; b] и F(x) первообразная функцией для функции f(x) на отрезке [a; b]. Тогда определенный интеграл от функции f(x) на [a; b] равен приращению первообразной на этом отрезке, т.е. .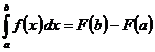

Ряды.

Основные понятия

Числовым рядом называется сумма вида

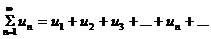
Где числа u₁, u₂, u₃, …. , u_n, … называемые членами ряда, образуют бесконечную последовательность; член u_n называют общим членом ряда.

Суммы:

. . . . . . . . . . .

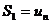
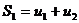
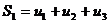
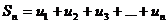
составленные из первых членов ряда, называются частичными суммами этого ряда.

Каждому ряду можно сопоставить последовательность частичных сумм S₁, S₂, S₃,…., S_n Если при бесконечном возрастании номера n частичная сумма ряда S_n стремится к пределу S, то ряд называется сходящимся, а число S – суммой сходящегося ряда, т.е.

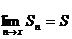или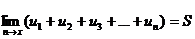

Эта запись равносильна записи

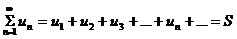
Если частичная сумма S_n ряда при неограниченном возрастании n не имеет конечного предела ( в частности, стремится к +х или к – бесконечность), то такой ряд называют расходящимся.

Если ряд сходится, то значение S_n при достаточно большом n является приближенным выражением суммы ряда S.

Разность r_n = S - S_n называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е. 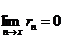, и наоборот, если остаток стремится к нулю, то ряд сходится.