Теорема Коши. Физический смысл.

Теорема: (Коши о среднем)

Пусть функции f(x) и g(x) непрерывны на отрезке [a,b] и имеют производные на интервале (a,b), одновременно не обращающиеся в ноль. При этом g(b)-g(a)¹0 (что следует из условия g΄(x)¹0). Тогда на интервале (a,b) найдется точка ζ, для которой выполняется неравенство:

, a<ζ<b.

Доказательство: Вводим функцию H(x)=(f(b)-f(a))·g(x)-(g(b)-g(a))·f(x). Очевидно, что она непрерывна на [a,b] и имеет производную на (a,b), т.к. f(b)-f(a) и g(b)-g(a) постоянны. Кроме того, H(a)=H(b), поэтому по теореме Ролля найдется такая точка ζ из (a,b), что H΄(ζ)=0.

H΄(ζ)=(f(b)-f(a))·g΄(ζ)-(g(b)-g(a))·f΄(ζ)Þ(f(b)-f(a))·g΄(ζ)=(g(b)-g(a))·f΄(ζ) , т.к. по условию g(b)-g(a)¹0 и g΄(x)¹0 на (a,b).

Теорема доказана.

Физический смысл: Если f΄(x) и g΄(x) – скорости, то отношение перемещений равно отношению скоростей в какой-то момент времени.

Билет 14

Теорема о среднем Лагранжа.

Теорема:

Пусть функция 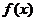непрерывна на отрезке и имеет производную на интервале . Тогда существует на интервале точка 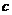, для которой выполняется равенство

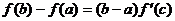(1),

причем .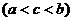

Доказательство:

В теореме Коши, возьмем 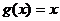. Тогда , , .

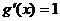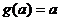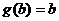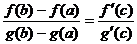
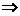
Из теоремы Коши: 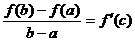теорема доказана.

Физический смысл:

Найдется момент времени когда 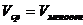(средняя скорость равна мгновенной)

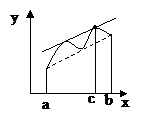Геометрический смысл:

Теорема Лагранжа утверждает, что если кривая есть график непрерывной на функции, имеющей производную на , то на этой кривой существует точка, соответствующая некоторой абсциссе 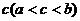такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы криво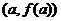й и .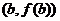

Равенство (1) называется формулой (Лагранжа) конечных приращений. Промежуточное значение 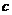удобно записывать в ви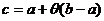де , где есть некоторое число, удовлетворяющее неравенствам 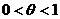. Тогда формула Лагранжа примет вид

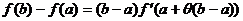
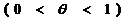
Она верна, очевидно, не только для 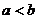, но и для .

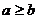Билет 15

Достаточное условие невозрастания (неубывания) функции на отрезке. Условие постоянства функции на отрезке.

Определение: Функция 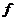называется строго возрастающей на отрезке [a,b], если для любых точек 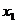, 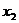из [a,b], удовлетворяющих неравенству , имеет место неравенство .

Определение: Функция 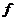называется неубывающей на [a,b], если из того, что и следует, что .

Определение: Функция 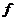называется строго убывающей на отрезке [a,b], если из того, что и следует, что .

Определение: Функция 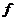называется невозрастающей на [a,b], если из того, что и следует, что .

Пример:

Если 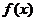убывает на и на , то нельзя говорить, что 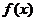убывает на .

Теорема 1: (необходимое условие возрастания (неубывания) функции в точке )

Если функция 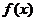возрастает (неубывает) в точке и дифференцируема в , то .

Доказательство:

Теорема доказана.

Пример: возрастает в 0 и

Теорема 1’: (необходимое условие убывания (невозрастания) функции в точке )

Если функция 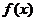убывает (невозрастает) в точке и дифференцируема в , то .

Доказательство – аналогично теореме 1.

Теорема 2: (достаточное условие возрастания)

Если функция 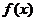дифференцируема в и , то 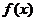возрастает в точке .

Доказательство:

возрастает.

Теорема доказана.

Замечание: Если в точке , то ни про возрастание, ни про убывание ничего сказать нельзя.

Билет 16