Теорема Лагранжа,теорема Коши
Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция непрерывна на отрезке[a,b] и дифференцируема в интервале(a,b) , то найдётся такая точка c э (a,b) , что 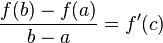 Геометрически это можно переформулировать так: на отрезке[a,b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Геометрически это можно переформулировать так: на отрезке[a,b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Доказательство
Для функции одной переменной:
Введем функцию 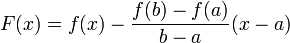 . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равныf(a) . Воспользовавшись упомянутой теоремой, получим, что существует точка , в которой производная функции F равна нулю:
. Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равныf(a) . Воспользовавшись упомянутой теоремой, получим, что существует точка , в которой производная функции F равна нулю:
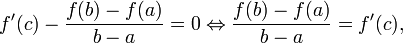
что и требовалось доказать.
Теорема Коши
1)Пусть f(x),g(x) определены на [a,b]
2)сущ-ют производныеf’(x),g’(x) на интервале(a,b)
3)g’(x) не равно 0,любое Х э [a,b],тогда
Существует С, a<c<b, f’(c)/g’(c)=f(b)-f(a)/g(b)-g(a)
Док-во
g(b) не равно g(a)
составимвспомогательнуюфун-июF(x)=f(x)-f(a)-f(b)-f(a)/g(b)-g(a)*(g(x)+g(a)) непрерывнаF’(x)=f’(x)-f(b)-f(a)/g(b)-g(a)*g’(x)
F(a)=f(a)-f(a)-(f(b)-f(a)/g(b)-g(a))*(g(a)-g(a))=0
F(b)=f(b)-f(a)-(f(b)-f(a)/g(b)-g(a))*(g(b)-g(a))=0
Сущ-етСF’(c)=0 отсюдаследуетf’(c)-(f(b)-f(a)/g(b)/g(a))*g’(c)=0
F’(c) /g’(c)=f(b)-f(a)/g(b)-g(a)
Дифференциалывысшихпорядков.
ФормулаЛейбница
Пусть y=f(x) дифференцируема функция, а ее аргумент х – независимая переменная. Тогда дифференциал dy=f ′(x)dx есть также функция х, можно найти дифференци-ал этой функции. Дифференциал от дифференциала есть второй дифференциал.
Производную можно рассматривать, как отношение дифференциала соответствующего порядка к соответ-ствующей степени дифференциала независимой пере-менной.
Дифференциал n-ого порядка, есть дифференциал от дифференциала (n-1)-ого порядка, т.е. производную функции можно рассматривать, как отношение ее диф-ференциала соответствующего порядка к соответству-ющей степени дифференциала независимой перемен-ной.
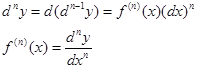
Понятие производной произвольного порядка задаётся рекуррентно. Полагаем
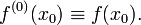
Если функция дифференцируема в , то производная первого порядка определяется соотношением
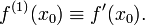
Пусть теперь производная -го порядка определена в некоторой окрестности точки и дифференцируема. Тогда
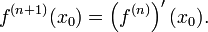
Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).
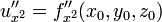 или
или 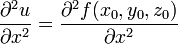
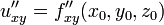 или
или 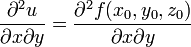
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,
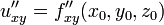
Формула Лейбница
Y^(n)=(U*V)^n=Сумма (от nдоk=0) U^(n-k)*V^(k)
Вторая производная для функции, заданной параметрически
(f’(x))’-производная второго порядка
F’’(x); Y’’=d^2y/dx^2
29. Правило Лопиталя:
Правило Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Условия
1. 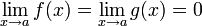 или
или 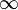
2.f(x)и g(x)дифференцируемы в проколотой окрестности 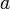
3. 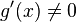 в проколотой окрестности
в проколотой окрестности 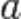
4. существует 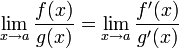
Пределы также могут быть односторонними.
Теорема.
Пустьf(x),g(x) непрерывны и дифференцируемы в окрестности т.а и равны нулю в этой точке. Пусть g’(a)не равно нулю,тогда если сущ-етlimf’(x)/g’(x)=l,то limf(x)/g(x)= limf’(x)/g’(x)=l
Замечание 1.
Теорема верна в том случае,если ф-и f(x) и g(x) не определены в точке а,носущ-етlimf(x)=0,limg(x)=0
Замечание 2.
Т.верна в том случае,если х принадлежит 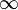
Замечание 3
Если limf’(x)/g’(x)=0/0 дифференцирование можно повторить еще раз
