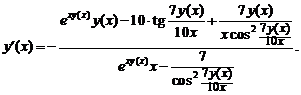Первый замечательный предел.
Можно показать, что справедливо соотношение, называемое первым замечательным пределом:
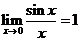 .
.
Рассмотрим на примере, как можно использовать данную формулу для разрешения особенностей тригонометрических функций в конечных точках.
Задача 2.1.в. Вычислить
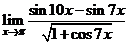 .
.
Решение. Убедимся, что мы имеем дело с неопределенностью вида 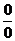 . При
. При 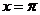 получаем:
получаем:
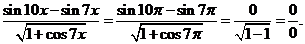
Прежде всего, сделаем замену переменной 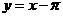 , так, чтобы новая переменная
, так, чтобы новая переменная 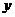 стремилась к 0, когда
стремилась к 0, когда 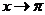 :
:
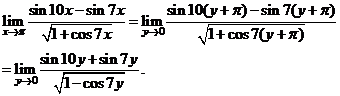
Используя формулу преобразования суммы синусов в произведение и формулу для косинуса двойного угла, получаем
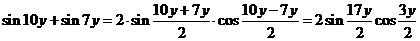
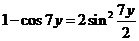 .
.
Отсюда
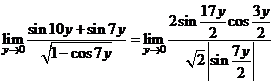 .
.
Пусть сначала 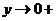 , тогда
, тогда 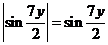 . Чтобы свести полученное выражение к формуле
. Чтобы свести полученное выражение к формуле 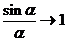 , поделим и умножим
, поделим и умножим 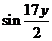 на
на 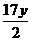 , а
, а 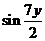 на
на 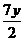 :
:
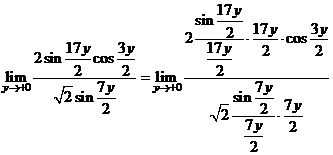
Заменяя пределы дробей 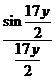 и
и 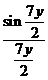 на 1, получаем
на 1, получаем
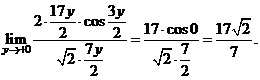
При 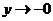 имеем
имеем 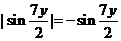 , и предел отличается только знаком:
, и предел отличается только знаком:
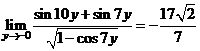 .
.
Второй замечательный предел.
Справедлива формула
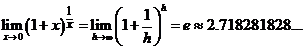
Задача 2.1.г.Вычислить 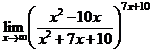 .
.
Решение. Выделим в основании показательной функции выражение вида 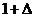 , где
, где 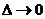 при
при 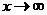 . Для этого прибавим и вычтем 1 из
. Для этого прибавим и вычтем 1 из 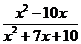 :
:
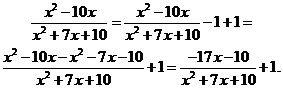
Получаем:
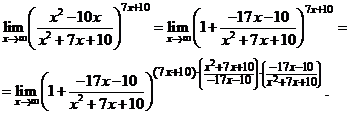
Используя формулу второго замечательного предела, заменим выражение 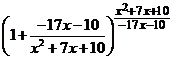 в пределе при
в пределе при 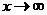 на
на 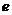 :
:
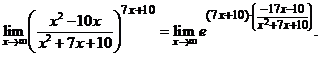
Осталось найти предел показателя степени:
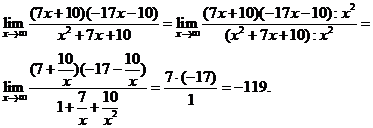
Ответ: 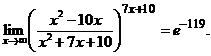
Комбинация первого и второго замечательных пределов.
Задача 2.1.д.Вычислить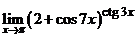 .
.
Решение. Убедимся сначала, что мы имеем дело с неопределенностью вида 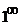 . Предел основания степени равен
. Предел основания степени равен 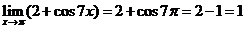 .Предел показателя степени равен
.Предел показателя степени равен 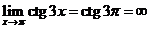 .Неопределенность вида
.Неопределенность вида 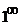 указывает, что для ее раскрытия следует воспользоваться вторым замечательным пределом. Выделим структуру второго замечательного предела
указывает, что для ее раскрытия следует воспользоваться вторым замечательным пределом. Выделим структуру второго замечательного предела 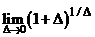 в нашей формуле:
в нашей формуле:
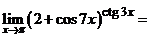
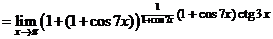
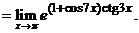
Теперь остается найти предел показателя степени. Делая замену переменной 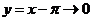 , получаем
, получаем
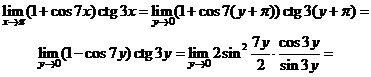
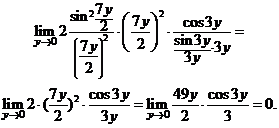
Ответ: 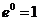 .
.
Особенность вида 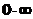 .
.
Задача 2.1.е.Вычислить 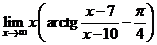
Решение. Чтобы свести данный предел к формуле первого замечательного предела, проведем следующее преобразование:
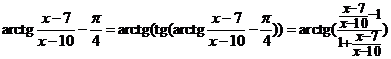 .
.
Мы воспользовались формулой
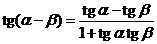 .
.
Поскольку
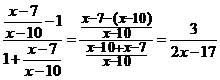 ,
,
получаем
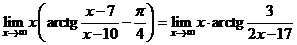 .
.
Остается сделать замену 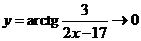 , откуда
, откуда 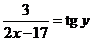 ,
, 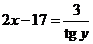 ,
, 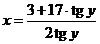 .
.
В результате получаем
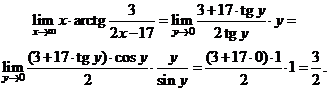
Ответ: 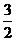 .
.
Производные.
Производной функции 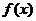 в точке
в точке 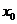 называется предел
называется предел
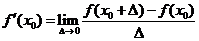 .
.
Наряду с обозначением 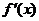 для производной используется еще обозначение
для производной используется еще обозначение 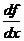 .
.
Производные основных элементарных функций приведены в следующей таблице.
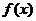 | 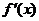 |
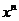 | 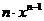 |
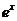 | 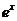 |
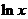 |  |
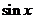 | 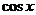 |
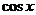 |  |
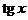 | 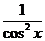 |
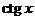 | 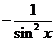 |
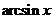 | 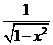 |
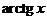 | 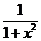 |
Рассмотрим дифференцирование степенной функции при некоторых 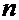 .
.
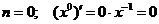
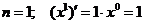
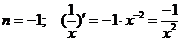
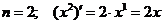
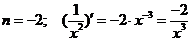
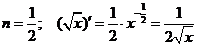
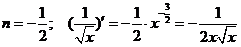
Имеется два основных приема дифференцирования функций
1) Формуладифференцирования произведения и частного двух функций
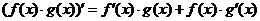 ,
,
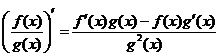 .
.
2) Формула дифференцирования композиции (или сложной функции)
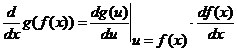 .
.
Примеры дифференцирования сложной функции.
1°) 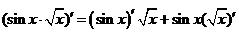
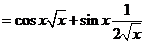
2°) 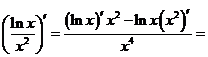
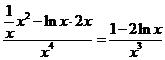
3°) 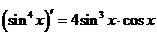
4°) 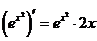
5°) 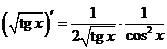
6°) 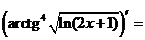
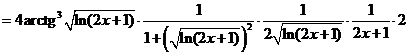
В задачах 2.2.а-2.2.з для функции 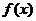 требуется найти производную
требуется найти производную 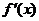 .
.
Задача 2.2.а 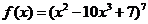 .
.
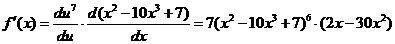 .
.
Задача 2.2.б 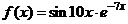 .
.
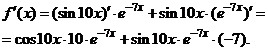
Задача 2.2.в 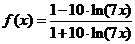 .
.
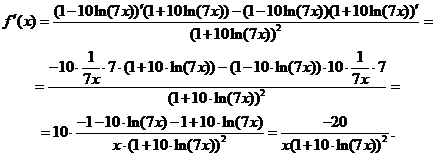 Задача 2.2.г
Задача 2.2.г 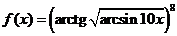 .
.
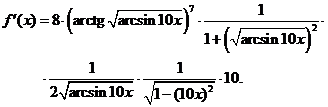
Задача 2.2.д 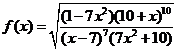 .
.
Решение.При дифференцировании этой функции удобно воспользоваться приемом, который называется логарифмическим дифференцированием. Прежде чем вычислять производную, найдем логарифм функции 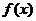 :
:
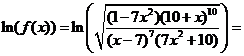
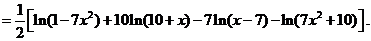
Теперь продифференцируем правую и левую часть полученной формулы, а затем приравняем соответствующие производные. Имеем:
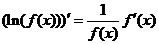 ;
;
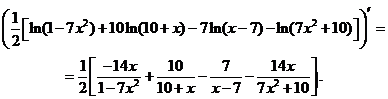
Отсюда,
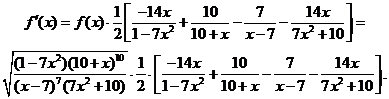
Задача 2.2.е 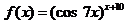 .
.
Решение.Здесь также удобно воспользоваться приемом логарифмического дифференцирования.
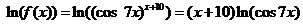 ;
;
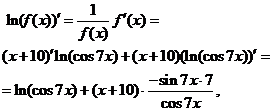
откуда следует, что
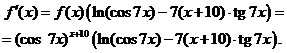
Задача 2.2.ж 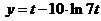 ,
, 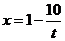 .
.
Решение.Функция 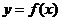 задана в параметрической форме, поэтому следует воспользоваться формулой для параметрической производной:
задана в параметрической форме, поэтому следует воспользоваться формулой для параметрической производной:
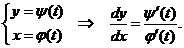
Получаем:
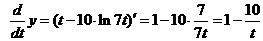 ,
,
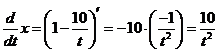 ,
,
откуда
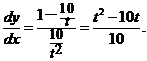
Задача 2.2.з 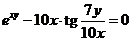 .
.
Решение.Функция 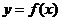 задана неявным уравнением. Чтобы найти производную
задана неявным уравнением. Чтобы найти производную 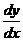 , продифференцируем тождество
, продифференцируем тождество 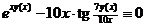 . Получаем:
. Получаем:
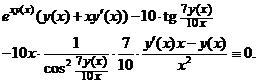
Перегруппируем слагаемые, выделяя члены, содержащие производную 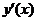 :
:
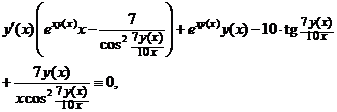
откуда следует, что