Прогнозирование по уравнению регрессии. Вероятностная оценка прогноза.
Прогнозирование осуществляется путем подстановки заранее спрогнозированного или ожидаемого значения факторного признака Х п р . Затем делаем оценку прогноза. Средняя возможная ошибка прогноза ,где
Определяем предельную ошибку прогноза . Рассчитаем доверительный интервал
35. Задачи статистического изучения динамики. Понятие временного ряда. Виды временных рядов, порядок обеспечения их сопоставимости. Графики временных рядов.
Управление любыми процессами (соц, эк., прир-ми), их научное предвидение тесно связаны с изучением изм-я этих процессов во t. Изучение процессов во t в ст-ке наз-ся изучением динамики. Методы изуч-я дин-ки позволяют решать задачи: выявление устойч. закон-тей в развитии процесса во t; аналитич. описание выявлен. законом-тей разв-я; хар-ка особенностей этих законом-тей; изуч-е, регламент, содерж-ий в уровнях любых проц-в дин-ки; опред-е силы этих колебаний и колич оценка колебл-ти; хар-ка типа колеб-ти; прогн-е проц-в по выявленной тенденции развития; оценка тренд. прогноза; оценка прог-за с учетом случ. колеб-й; изуч-е сез-х особ-тей разв-я процесса; колич. хар-ка колеб-й уровня врем-х рядов; прогн-е проц-в с учетом сезон-х колеб-й и др. Изуч-е процесса во t треб-ет особой ориент-ии инф. базы и особых форм сбора инфо. Д/изуч-я процесса /объекта во t, стат. совокуп-ть должна формир-ся из сведений о состоянии этого процесса/объекта, кот. получены при последоват. многоразовых наблюдениях за ним в течен. длит. периода t. При этом, чем чаще собираются сведения об объекте, тем более подробная хар-ка будет получена. Множ-во знач-ий одного признака, зафиксированные за последоват. отрезки / моменты t, образуют временной / динамич. ряд. Времен. ряд – таблица, в кот. приводятся отрезки / моменты t, признаки / знач-я пок-ля, сформированные за эти временные хар-ки. Каждое конкр. знач-е пок-ля – уровень времен. ряда. Виды врем. рядов:
- интервальные (построен. из множ-ва знач.пок-ля, сформирован. за опр. отрезки t – год, квартал, мес. Знач-е их Ур-ней формир-ся за указан. отрезки t) и моментные (ряды, построенные из множ-ва знач-ий пок-ля, приведенных на опр. дату (напр, на начало/конец года). Значение Ур-ней измер-ся в опр.моменты t).
- абсол.пок-лей(построен по знач-ю первич приз-в) и относит.пок-лей(постр по знач-ю вторич приз-в). Ряды разного вида не сопоставимы др. с др. Но несопоставимость интервал. и моментных можно преодолеть. Д/этого моментн. ряды преобраз. к виду, схожему с интервал., путём расчета сред. ур-ня момент. ряда за период t. Если моментн. ряд приведен на начало года – такой можно привести к виду, схожему с интервальным, путём расчеты ср. ур-ня за отрезок t
у1 янв уi – данный месяц
у1 фев yi+1 – след.месяц
у1 мар
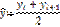
если момент. врем. ряд приведен на конец отрезка t, тогда сред. уровень:
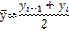уi-1 – предыдущ. Месяц
График построен правильно, если его раз-р по оси у в 2 раза меньше по оси х. Если необ-мо пост-ть на 1ой корд. пл-ти 2 разных графика и их ур-ни взаимос-ны, имеют разную ед-цу изм-я, то графики стр-ся по базисным темпам роста одинак-го показ-ля.