Угол между прямыми на плоскости.

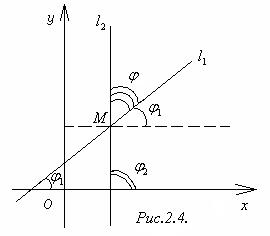Рассмотрим на плоскости две прямые R₁ : y = k₁x + b₁ и R₂ : y = k₂x + b₂ с углами наклона к оси Ox соответственно φ₁ и φ₂ (рис.2.4).

Определение 2.2. Углом между прямымиR₁ и R₂ будем называть меньший из смежных углов, образованных этими пересекающимися прямыми.

На рис.2.4 таким является угол φ. Очевидно, что

0 ≤ φ ≤ 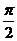. Из геометрических соображений устанавливаем зависимость между углами φ₁, φ₂ и φ : φ = φ₂ – φ₁. Возможны два случая:

1) Угол φ = 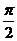, т.е. прямые R₁ и R₂ перпендикулярны.

2) 0 ≤ φ < 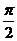. Тогда tg φ = tg (φ₂ – φ₁) = =

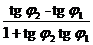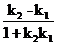
Формула

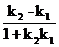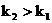tg φ = , где (7)

позволяет вычислить угол между неперпендикулярными прямыми.

Условия параллельности и перпендикулярности прямых на плоскости.

1) Если прямые R₁ и R₂ параллельны, то φ = 0. Тогда tg φ = 0 и из формулы (7) имеем k₂ - k₁ = 0 или k₂ = k₁. Таким образом, условием параллельности двух прямых на плоскости является равенство их угловых коэффициентов.

2) Если прямые R₁ и R₂ перпендикулярны, то φ = 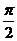. Так как φ = φ₂ – φ₁ , то

φ₂ = 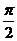+ φ₁ и tg φ₂ = tg( 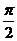+ φ₁) = ctg φ₁ = - 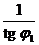, т.е.

k₂ = - 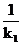. (8)

Таким образом, условие перпендикулярности двух прямых состоит в том, что их угловые коэффициенты обратны по величине и противоположны по знаку.

Расстояние от точки до прямой.

Теорема 3.1.Расстояние d от данной точки М(х₀;у₀) до прямой ℓ, заданной уравнением

Ах + Ву + С = 0 на плоскости определяется формулой

d = 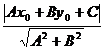. (1)

Доказательство. Пусть в прямоугольной системе координат прямая ℓ имеет уравнение Ах + Ву + С = 0, а точка М ─ координаты (х₀;у₀). Возьмём на прямой ℓ две произвольные точки Е(х₁;у₁) и F(х₂;у₂). Нетрудно заметить, что

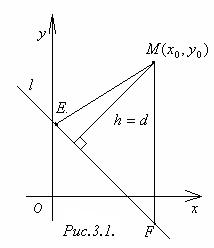d = h = .

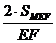По формуле (6) лекции 1 имеем

S_MEF = 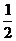│(x₂ – x₁)(y₀ – y₁) – (x₀ – x₁)(y₂ – y₁)│.

По формуле расстояния между точками на плоскости

EF = .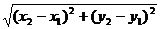

Тогда

d = 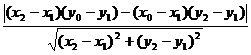. (2)

Запишем уравнение прямой ℓ по двум точкам E и F:

.

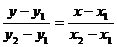Преобразуем это уравнение в общее уравнение прямой:

(у – у₁)(х₂ – х₁) = (х – х₁)(у₂ – у₁),

(у₂ – у₁)х + (х₁ – х₂)у + (у₁(х₂ – х₁) – х₁(у₂ – у₁)) = 0.

По условию, общее уравнение прямой ℓ имеет вид Ах + Ву + С = 0, следовательно,

А = m(y₂ – y₁),

B = m(x₁ – x₂),

C = m(у₁(х₂ – х₁) – х₁(у₂ – у₁)).

для некоторого целого числа m ¹ 0.

Тогда из (2) имеем

d = ==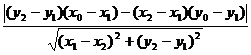

= = =

= =

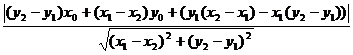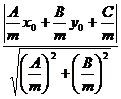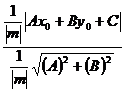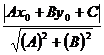
Взаимное расположение двух прямых на плоскости.

Пусть прямые ℓ₁ и ℓ₂ заданы своими общими уравнениями. Рассмотрим эти уравнения как систему двух уравнений первой степени с двумя неизвестными х и у:

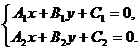(3)

Решаем эту систему:

а)

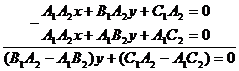
(А₁В₂ – А₂В₁)у = С₁А₂ – А₁С_{2 .} (4)

б)

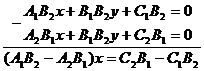(5)

Возможны следующие случаи:

1) А₁В₂ – А₂В₁ ¹ 0 т.е. А₁В₂ ¹ А₂В₁ Þ 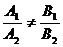. Тогда из формул (4) и (5) находим единственное решение системы (3):

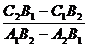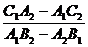х = , у = . (6)

Единственное решение системы (3) означает, что прямые ℓ₁ и ℓ₂ пересекаются. Формулы (6) дают координаты точки пересечения.

2) А₁В₂ – А₂В₁ = 0 т.е. А₁В₂ = А₂В₁ Þ .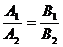

2.1) С₂В₁ – С₁В₂ = 0 и С₁А₂ – А₁С₂ = 0.

Тогда А₁В₂ = А₂В₁, С₂В₁ = С₁В₂ и С₁А₂ = А₁С₂, откуда , , .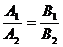

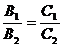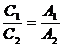Таким образом, 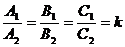. Тогда А₁ = kA₂, B₁ = kB₂, C₁ = kC₂. Теперь, уравнение прямой ℓ₁ имеет вид:

kA₂x + kB₂y + kC₂ = 0

или

A₂x + B₂y + C₂ = 0.

Следовательно, прямые ℓ₁ и ℓ₂, имея одно и то же уравнение, совпадают.

2.2) С₂В₁ – С₁В₂ ¹ 0 или С₁А₂ – А₁С₂ ¹ 0.

Пусть, для определённости С₂В₁ – С₁В₂ ¹ 0, т.е. С₂В₁ ¹ С₁В₂ Þ 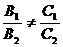. Тогда равенство (5) имеет вид 0 × х = С₂В₁ – С₁В₂. Следовательно, это уравнение, а значит и система (3) решений не имеет. Это означает, что прямые ℓ₁ и ℓ₂ на плоскости не пересекаются, т.е. они параллельны. Аналогичный вывод можно сделать в случае, когда С₁А₂ – А₁С₂ ¹ 0.

Итак, если:

1) 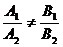, то прямые ℓ₁ и ℓ₂ пересекаются в точке с координатами (6);

2) 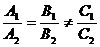, то прямые ℓ₁ и ℓ₂ параллельны;

3) 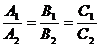, то прямые ℓ₁ и ℓ₂ совпадают.

Эллипс. Окружность.

Определение 4.1. Эллипсомназывается множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.

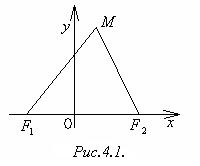Пусть F₁(-c,0) и F₂(c,0) ─ фокусы. Тогда F₁F₂ = 2c ─ фокусное расстояние(рис.4.1). Постоянную величину, о которой идёт речь в определении эллипса, обозначим 2a.

Пусть M(x,y) ─ произвольная точка эллипса. Тогда по определению F₁M + F₂M = 2a > 2c, откуда a > c.

Так как F₁M = 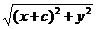, F₂M = 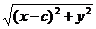, то имеем уравнение 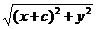+ 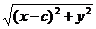= 2a.

Преобразуем это уравнение:

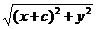( )² = (2a − 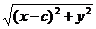)² ,

(x² + 2cx + c²) + y² = 4a² – 4a 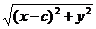+ (x² –­ 2cx + c²) + y²,

a 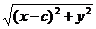= a² – cx.

Возводя в квадрат последнее уравнение, имеем

a²(x² – 2cx + c² + y²) = a⁴ – 2cxa² + c²x²,

(a² – c²)x² + a²y² = a²(a² – c²).

Так как a > c, то a² – c² > 0 и можем обозначить b² = a² – c². Тогда

b²x² + a²y² = a²b²,

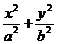= 1 (1)

Таким образом, координаты любой точки эллипса удовлетворяют уравнению (1).

Покажем обратное: если координаты точки M(x,y) удовлетворяют уравнению (1), то точка M лежит на эллипсе.

Из (1) найдём y² : y² = b²(1 - ).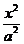

Тогда F₁M = = = = = = = │ │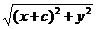

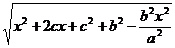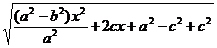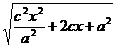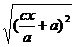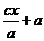Т.к. c < a и из (1) 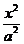≤ 1, т.е. x² ≤ a² , │x│ ≤ a, то 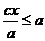. Следовательно,

│ │= .

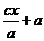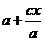Аналогично можно вычислить

F₂M = .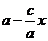

Теперь

F₁M + F₂M = .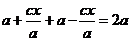

Из уравнения (1) : b² > 0 Þ a² – c² > 0, т.е. a > c, откуда 2a > 2c. Значит, точка M лежит на эллипсе.

Уравнение (1) называется каноническим уравнением эллипса.Изображён эллипс с уравнением (1) на рис 4.2.

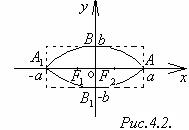Точки пересечения эллипса с осями координат называются вершинами эллипса.Оси симметрии эллипса (оси Ox и Oy) называют осями эллипса. Точка пересечения осей ─ центр эллипса. Осяминазывают также отрезки A₁A, B₁B. Отрезки OA, OB и их длины называют полуосями. В нашем случае a > b, поэтому а называют большой полуосью,b ─ малой полуосью. Эксцентриситетом эллипсаназывается отношение фокусного расстояния к длине большой оси, т.е.

ε = .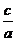

Так как 0 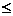c < a, то 0 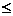ε < 1. Фокальными радиусами точки Mназывают отрезки F₁M и F₂M. Их длины r₁ и r₂ вычисляют по формулам

r₁ = a + εx,

r₂ = a – εx.

Уравнение (1) можно рассматривать и в случае, когда b > a, оно определяет эллипс с большой полуосью OB = b, фокусы такого эллипса лежат на оси Oy, причём a² = b² – c².

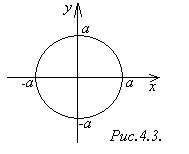
В случае, когда a = b, уравнение (1) принимает вид

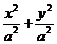= 1 или x² + y² = a²

и определяет окружность радиуса а с центром в начале координат (рис.4.3). В этом случае c = 0, поэтому ε = 0.

Из школьного курса известно уравнение окружности радиуса R с центром в точке A₀(x₀,y₀):

(x – x 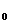) 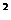+(y – y 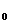) 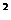=R .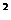

Такое уравнение называют каноническим уравнением окружности.

Гипербола.

Определение 4.2. Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек, называемыхфокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

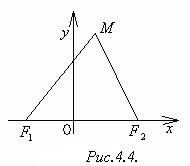
Пусть F₁(-c,0) и F₂(c,0) ─ фокусы. Тогда F₁F₂ = 2c ─ фокусное расстояние (рис.4.4). Постоянную величину, о которой идёт речь в определении, обозначим 2a. Тогда по определению 2a < 2c, т.е. a < c.

Пусть M(x;y) ─ произвольная точка гиперболы. Рассуждая по аналогии с п. 4.1, можем получить уравнение

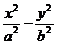= 1, (2)

где b² = c² – a².

Уравнение (2) называют каноническим уравнением гиперболы. Гипербола с уравнением (2) изображена на рис.4.5.

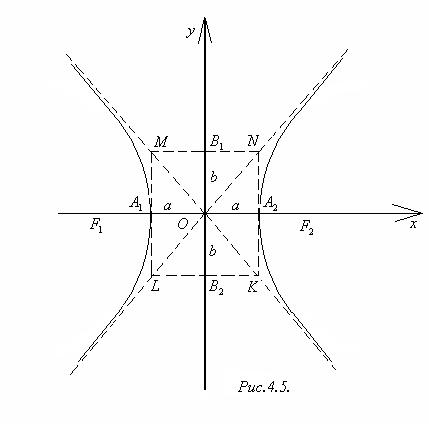
Прямоугольник MNKL, стороны которого MN = LK = 2a, ML = NK = 2b, называется основным прямоугольником. Прямые MK и NL называют асимптотами гиперболы,их уравнения : y = – 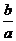x и y = 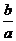x, соответственно. Гипербола имеет две ветви: левую и правую. Центр симметрии гиперболы называется её центром. Оси симметрии гиперболы называются её осями. Одна ось пересекает гиперболу в двух точках (на рис.4.5 это т. A₁ и A₂), эта ось называется действительной осью гиперболы,другая ось ─ мнимой осью, она не имеет общих точек с гиперболой. Длины отрезков A₁A₂ и B₁B₂ также называют осями. Величины a и b называются полуосями гиперболы. Если a = b, то гипербола называется равносторонней,её уравнение

x² – y² = a².

Уравнение

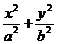- = 1 (3)

определяет гиперболу с действительной осью Oy (рис.4.6).

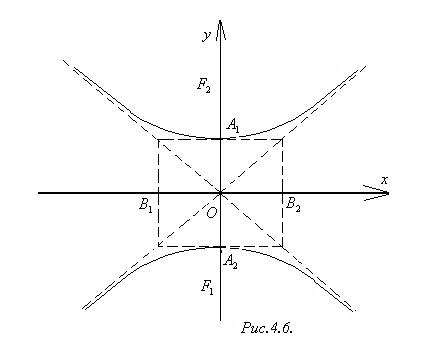
Гиперболы, определяемые уравнениями (2) и (3) в одной и той же системе координат, называются сопряжёнными. Эксцентриситет гиперболы─ это отношение фокусного расстояния к расстоянию между вершинамигиперболы (т.е. точками пересечения гиперболы с осями). Для уравнения (2)

ε = .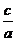

Так как c > a, то ε > 1. Фокальные радиусы точки M гиперболы─ это отрезки F₁M и F₂M. Их длины r₁ и r₂ для правой ветви

r₁ = εx + a, r₂ = εx – a,

для левой ветви

r₁ = -εx − a, r₂ = - εx + a.

Парабола.

Определение 4.3. Параболойназывается множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и данной прямой, называемой директрисой, и не проходящей через фокус.

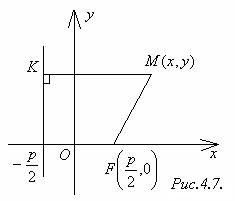
Возьмём в прямоугольной системе координат точку F( 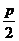,0), где p > 0 и пусть она будет фокусом. Директрисой будет прямая x = - 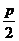(рис.4.7). Пусть M(x,y) ─ произвольная точка параболы. Если K ─ основание перпендикуляра из точки M к директрисе, то она имеет координаты (- 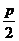,y). По определению 4.3

MK = MF.

Тогда

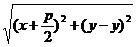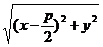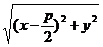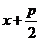= , = , т.к. x ≥ 0.

Возводим уравнение а квадрат и приводим подобные члены:

,

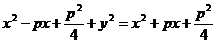y² = 2px (4)

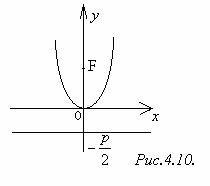
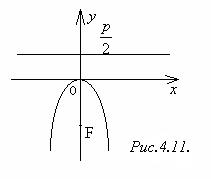
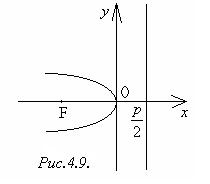
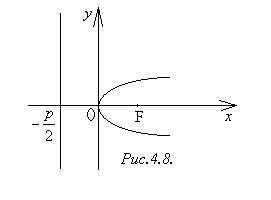Уравнение (4) называется каноническим уравнением параболы. Величину p называют параметром параболы. Парабола с уравнением (4) изображена на рис.4.8. Точка O называется вершиной параболы,ось симметрии ─ осью параболы. Если парабола имеет уравнение y² = - 2px, то её график расположен слева от оси Oy (рис.4.9). Уравнения x² = 2pyи x² = -2py, p > 0 определяют параболы, изображённые на рис.4.10 и рис.4.11, соответственно.

Понятие о матрице.

Таблица чисел а_ik вида

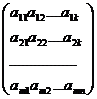, (1)

состоящая из m строк и n столбцов называется матрицей размера m × n. Числа а_ik называются её элементами. Если m ¹ n, то матрица называется прямоугольной.Если же

m = n, то матрица называется квадратной.В частности, если m = 1, n > 1, то матрица

(а₁₁ а₁₂ … а_1n) называется матрицей-строкой. Если же m > 1, n = 1, то матрица называется матрицей-столбцом.

Число строк в квадратной матрице называют порядком такой матрицы. Например, матрица 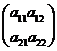есть квадратная матрица второго порядка, а матрица 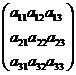есть квадратная матрица третьего порядка.

Матрицы будем обозначать большими латинскими буквами. Две матрицы A и B называются равными (А = В), если они одинакового размера и их соответствующие элементы равны. Так, если А = 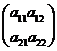, В = 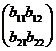и а₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁, a₂₂ = b₂₂, то А = В.