Размерность и базис векторного пространства

Определение. Вектор 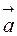называется линейной комбинацией векторов 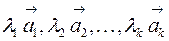векторного пространства R, если он равен сумме произведений этих векторов на произвольные действительные числа:

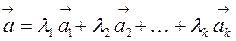(8.1)

где 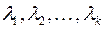– какие угодно действительные числа.

Определение. Векторы 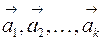векторного пространства 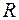называются линейно зависимыми, если существуют, такие числа 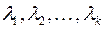, не равные одновременно нулю, что:

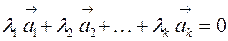(8.2)

В противном случае векторы 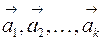называются линейно независимыми.

Из приведенных выше определений следует, что векторы 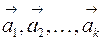линейно независимы, если равенство 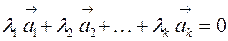справедливо лишь при 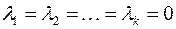, и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел 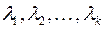отлично от нуля.

Можно показать, что если векторы 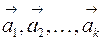линейно зависимы, то, по крайней мере, один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы. В противном случае векторы 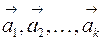называются линейно независимыми.

Из приведенных выше определений следует, что векторы 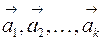линейно независимы, если равенство (8.2) справедливо лишь при 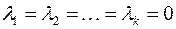, и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел 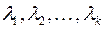отлично от нуля.

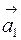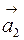Примером линейно независимых векторов являются два неколлинеарных, т.е. не параллельных одной прямой, вектора и на плоскости. Действительно, условие (8.2) 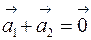будет выполняться лишь в случае, когда 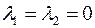, ибо если, например, 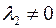, то 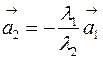и векторы 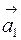и 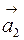коллинеарны. Однако любые три вектора плоскости линейно зависимы.

Отметим некоторые свойства векторов линейного пространства.

I.Если среди векторов 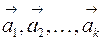имеется нулевой вектор, то эти векторы линейно зависимы.

II.Если часть векторов 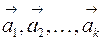являются линейно зависимыми, то и все эти векторы — линейно зависимые.

Определение. Линейное пространство 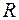называется -мерным, если в нем существует линейно независимых векторов, а любые из 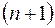векторов уже являются зависимыми. Другими словами, размерность пространства — это максимальное число содержащихся в нем линейно независимых векторов. Число называется размерностью пространства 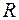и обозначается .

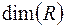Определение.Совокупность линейно независимых векторов -мерного пространства 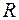называется базисом.

Справедлива следующая теорема.

Теорема. Каждый вектор линейного пространства 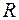можно представить и притом единственным способом в виде линейной комбинации векторов базиса :

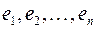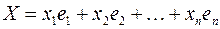
Это равенство называется разложением вектора по базису 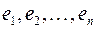, а числа 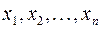— координатами вектора 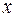относительно этого базиса. В силу единственности разложения каждый вектор однозначно может быть определен координатами в некотором базисе.

Очевидно, что нулевой вектор имеет все нулевые координаты, а вектор, противоположный данному, – противоположные по знаку координаты.

Теорема. Если 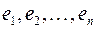– система линейно независимых векторов пространства 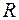и любой вектор линейно выражается через 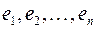, то пространство 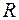является -мерным пространством 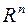, а векторы 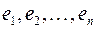– его базисом.

Базисом векторного пространства 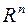называется любая независимая система линейно независимых –векторов этого пространства, количество которых равно , т.е. выбор системы базисных векторов векторного пространства 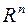неоднозначен, и может быть осуществлен большим числом способов.

Нередко приходится встречаться с заменой переменных, при которой старые переменные линейно выражаются через новые, например, при переходе от одного базиса пространства 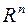к другому. Такую замену переменных называют обычно их линейным преобразованием.

Линейным преобразованием переменных называется выражение системы переменных 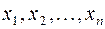через новую систему переменных 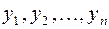с помощью линейных однородных функций:

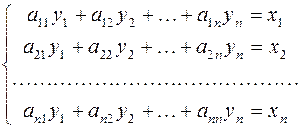
Линейное преобразование вполне определяется таблицей размером 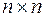, составленной из коэффициентов при 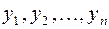. Такая таблица, составленная из элементов 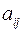называется матрицей 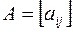, а само преобразование представляет собой пример матричной операции. Понятие матрицы требует более детального рассмотрения, что и будет сделано в следующем разделе.

Контрольные вопросы к лекции №8

1. Понятие евклидова пространства.

2. Линейная зависимость и линейная независимость векторов.

3. Понятия размерности и базиса линейного пространства.

4. Линейное преобразование векторов.

Лекция 9. Матрицы

Основные понятия:

матрица; элемент матрицы; размер матрицы; строка; столбец; квадратная матрица; главная диагональ; побочная диагональ; диагональная матрица; скалярная матрица; единичная матрица; нулевая матрица; сумма матриц; произведение матриц; согласованные матрицы; транспонирование матриц; определитель матрицы; минор; алгебраическое дополнение; линейная зависимость; линейная комбинация; ранг матрицы; окаймляющий минор; элементарные преобразования матрицы; обратная матрица.

Основные понятия

Прямоугольная таблица:

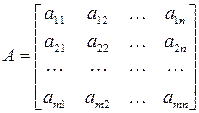(9.1)

состоящая из 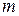строк и 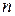столбцов, называется матрицей размера 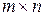или 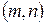-матрицей.

Матрицу (9.1) будем обозначать или 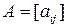. Числа 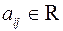называются элементами матрицы, индекс 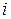обозначает номер строки, а индекс 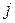‑ номер столбца, на пересечении которых расположен элемент.

Если 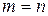, то матрица (9.1) называется квадратной матрицей порядка .

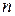В квадратной матрице 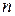-го порядка диагональ, состоящая из элементов 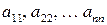называется главной диагональю, состоящая из элементов 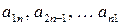‑ побочной диагональю.

Квадратная матрица:

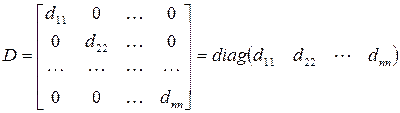
называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е. 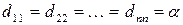, то такая матрица называется скалярной. Скалярная матрица, у которой 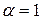называется единичной и обозначается буквой 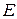. Например, единичная матрица третьего порядка:

.

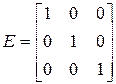Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.

Матрицы и 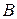называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.

Операции над матрицами

Суммой двух матриц 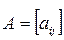и 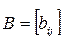одинакового размера называется матрица 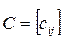того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е. .

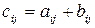Сложение матриц обладает следующими свойствами:

1.Коммутативность, т.е. .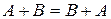

2.Ассоциативность, т.е. .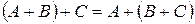

3.Для любых двух матриц и 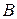одинакового размера существует единственная матрица 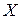такая, что 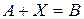. Матрица 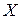обозначается 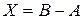и называется разностью матриц 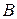и . Уравнение 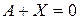имеет решение 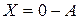, получающаяся при этом матрица называется противоположной и обозначается .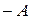

Произведением матрицы 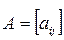на число 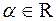называется матрица, все элементы которой равны соответствующим элементам матрицы , умноженным на число .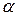

Умножение матрицы на действительное число обладает следующими свойствами:

1. ;

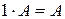2. ;

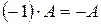3. ;

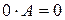4. 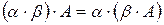(ассоциативность);

5. 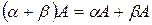(дистрибутивность);

6. 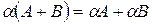(дистрибутивность).

Матрица называется согласованной с матрицей 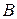, если число столбцов матрицы равно числу строк матрицы 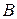. В этом случае произведением матрицы 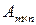на матрицу 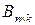называется матрица 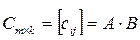, где 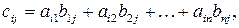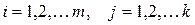, т.е. элемент, стоящий в 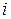-той строке и 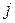-том столбце матрицы произведения равен сумме произведений элементов 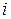-той строки матрицы на соответствующие элементы 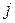-го столбца матрицы .

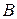Свойства умножения:

1.Если матрица согласована с матрицей 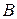, а матрица 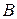согласована с матрицей 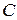, то 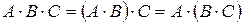‑ ассоциативность умножения;

2. 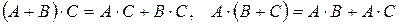‑ свойство дистрибутивности;

3. Умножение матриц не коммутативно, т.е., как правило, .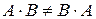

Транспонированием матрицы называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е. 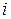-я строка матрицы становится 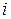-тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице обозначается .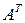

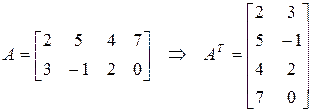
Свойства транспонирования:

1.

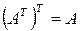
2.

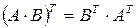
3.

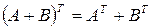
4.

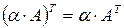
Определитель матрицы

Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.

Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 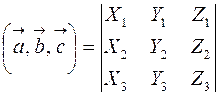, или в свернутой форме 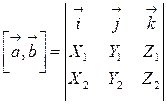. Предыдущая формула получается разложением определителя по первой строке.

Возьмем теперь квадратную матрицу 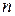-го порядка

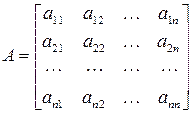(9.2)

Для записи определителя 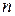-го порядка матрицы будем применять обозначения 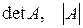. При 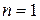матрица состоит из одного элемента и ее определитель равен этому элементу. При 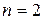получаем определитель .

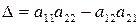Минором 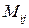элемента 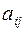матрицы называют определитель матрицы 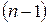-го порядка, получаемого из матрицы вычеркиванием 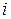-той строки и 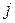-го столбца.

Пример 7. Найти минор 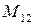матрицы:

.

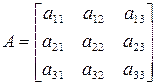По определению, минор 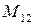элемента 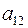есть определитель матрицы, получаемой из матрицы вычеркиванием первой строки и второго столбца. Следовательно, .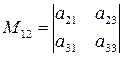

Алгебраическим дополнением элемента 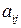матрицы называется минор 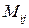, взятый со знаком 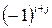. Алгебраическое дополнение элемента 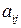обозначается 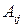, следовательно, .

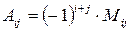Пример 8. Найти алгебраическое дополнение элемента 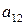матрицы из примера 7.

.

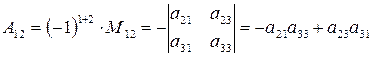Определителем квадратной матрицы 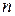-го порядка 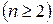называется число:

,

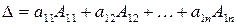(9.3)

где 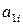‑ элементы первой строки матрицы (9.2), а 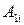их алгебраические дополнения .

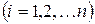Запись по формуле (9.3) называется разложением определителя по первой строке.

Рассмотрим свойства определителей.

Свойство 1. При транспонировании матрицы ее определитель не меняется.

Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:

Определителем квадратной матрицы 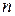-го порядка 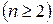называется число:

,

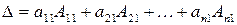(9.4)

где 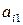‑ элементы первого столбца матрицы (9.2), а 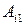их алгебраические дополнения .

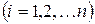Свойство 2. Если поменять местами две строки или два столбца матрицы , то ее определитель изменит знак на противоположный.

Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:

Определитель квадратной матрицы 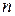-го порядка (будем в дальнейшем говорить определитель 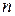-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.

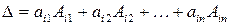, или .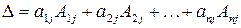

Свойство 3. Определитель, у которого две строки или два столбца одинаковы, равен нулю.

Действительно, поменяем в определителе 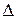две одинаковые сроки местами. Тогда, по свойству 2 получим определитель 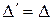, но с другой стороны, определитель не изменится, т.е. 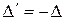. Отсюда .

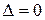Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя 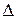умножить на число 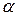, то определитель умножится на .

.

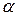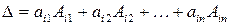Умножим элементы 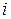-той строки на 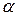. Тогда получим определитель:

.

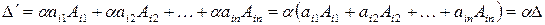Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.

Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.

Свойство 5. Определитель, у которого две строки (два столбца) пропорциональны, равен нулю.

Пусть 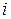-я строка пропорциональна 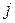-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.

Свойство 6. Если каждый элемент строки (столбца) определителя 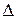есть сумма двух слагаемых, то определитель 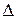равен сумме двух определителей: у одного из них 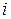-той строкой (столбцом)служат первые слагаемые, а у другого – вторые.

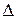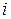Разложив определитель по -той строке получим:

.

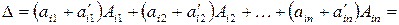
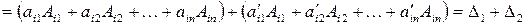Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Прибавив к элементам 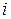-той строки определителя 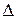соответствующие элементы 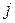-ой строки, умноженные на число 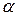, получим определитель 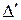. Определитель 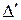равен сумме двух определителей: первый есть 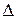, а второй равен нулю, так как у него 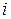-тая и 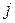-тая строки пропорциональны.

Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.:

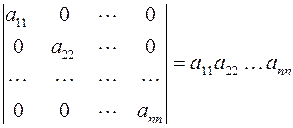
Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.

Рассмотрим вспомогательный определитель 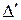, который получается из данного определителя 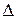заменой 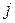-той строки 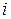-той строкой. Определитель 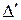равен нулю, так как у него две одинаковые строки. Разложив его по 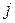-той строке получим:

.

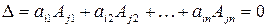Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.

Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.

Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т.е. .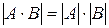

Ранг матрицы

Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы обозначают 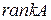или .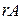

Если все миноры порядка 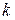данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.

Если все миноры первого порядка (элементы матрицы ) равны нулю, то 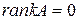. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то 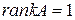. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка 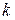, окаймляющие ненулевой минор 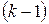-го порядка равны нулю, либо таких миноров нет. Тогда .

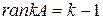Пример 10. Вычислить ранг матрицы .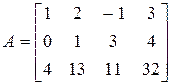

Минор первого порядка (элемент 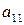) отличен от нуля. Окаймляющий его минор 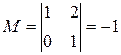тоже не равен нулю.

Далее рассмотрим миноры, окаймляющие минор :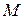

;

.

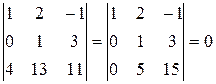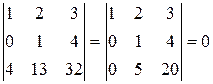Все эти миноры равны нулю, значит .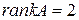

Приведенный алгоритм нахождения ранга матрицы не всегда удобен, поскольку связан с вычислением большого числа определителей. Наиболее удобно пользоваться при вычислении ранга матрицы элементарными преобразованиями, при помощи которых матрица приводится к столь простому виду, что очевидно, чему равен ее ранг.

Элементарными преобразованиями матрицы называют следующие преобразования:

Ø умножение какой-нибудь строки (столбца) матрица на число, отличное от нуля;

Ø прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число.

Полужордановым преобразованием строк матрицы:

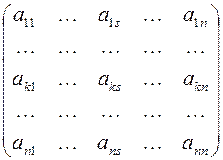
с разрешающим элементом 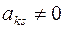называется следующая совокупность преобразований со строками матрицы:

Ø к первой строке прибавить 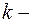ю, умноженную на число 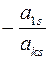и т.д.;

Ø к последней строке прибавить 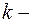ю, умноженную на число .

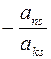После выполнения этих преобразований получается матрица:

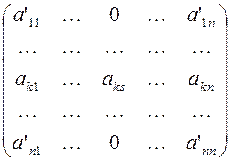
Полужордановым преобразованием столбцов матрицы с разрешающим элементом 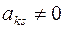называется следующая совокупность преобразований со столбцами матрицы:

Ø к первму столбцу прибавить 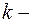й, умноженный на число 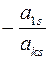и т.д.;

Ø к последнему столбцу прибавить 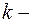й, умноженный на число .

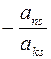После выполнения этих преобразований получается матрица:

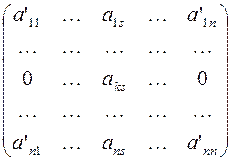
Полужорданово преобразование строк или столбцов квадратной матрицы не изменяет ее определителя.

Элементарные преобразования матрицы не изменяют ее ранга. Покажем на пример, как вычислить ранг матрицы, пользуясь элементарными преобразованиями.

Пример 11. Вычислить ранг матрицы .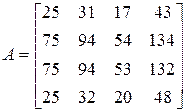

Применим к матрице элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.

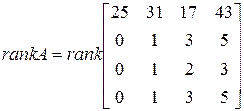
Вычитая далее вторую строку из третьей и последней, имеем:

.

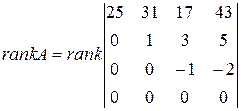Последняя матрица содержит отличный от нуля минор 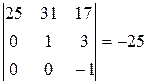третьего порядка, определитель же самой матрицы равен нулю. Следовательно, .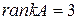

Отметим два важных свойства ранга матрицы:

· Ранг матрицы не меняется при ее транспонировании;

· Если ранг матрицы равен 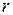, то любые ее 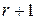строк (столбцов) линейно зависимы.

Обратная матрица

Пусть - квадратная матрица порядка 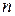. Матрица 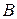называется обратной матицей к матрице , если выполняются равенства 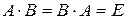, где 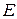‑ единичная матрица порядка .

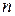Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.

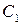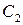Пусть и ‑ матрицы, обратные к матрице . Тогда 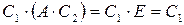, с другой стороны, .

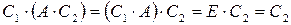Откуда 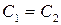. Обратную матрицу к матрице обозначают .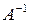

Теорема 2. Матрица имеет обратную матрицу тогда и только тогда, когда .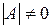

Пусть имеет обратную матрицу. Тогда 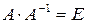и, применяя теорему об умножении определителей, получаем 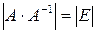или 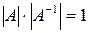. Следовательно, .

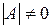Пусть 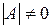. Укажем явное выражение матрицы 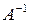через элементы матрицы , а именно: если 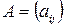, то:

,

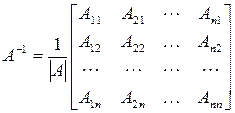(9.5)

здесь 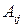‑ алгебраическое дополнение к элементу 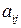. Матрица (9.5) получается из матрицы следующим образом. Сначала вместо каждого элемента 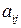пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную .

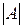Непосредственное умножение на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) – матрица, обратная к .

Пример 12. Найти обратную матрицу к матрице .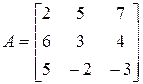

Так как 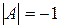, то 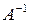существует. Вычислим алгебраические дополнения элементов матрицы :

,	,
,	,
,	,
,	,
.

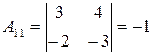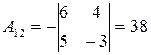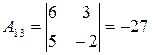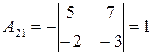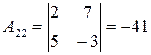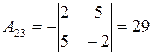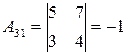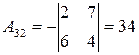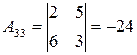Матрицу 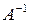находим в два приема, согласно формуле (9.5). Сначала запишем матрицу 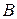, состоящую из алгебраических дополнений элементов . 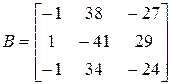Затем матрица 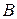транспонируется и умножается на число обратное 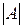, в данном случае – на (-1). Окончательно получаем:

.

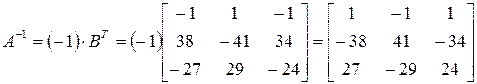Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если и 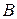‑ невырожденные матрицы одинакового порядка, то:

,

,

,

.

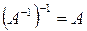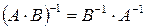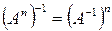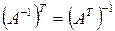Контрольные вопросы к лекции №9

1. Понятие матрицы.

2. Виды матриц.

3. Понятие транспонирования матриц.

4. Операции сложения и вычитания матриц.

5. Операции умножения и возведения в степень матриц.

6. Понятие определителя.

7. Определитель 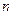- го порядка.

8. Правила нахождения определителей 2 и 3 порядка.

9. Свойства определителей.

10. Правила нахождения определителей 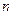- го порядка.

11. Понятие обратной матрицы.

12. Схема нахождения обратной матрицы.

13. Понятие ранга матрицы.