Размерность и базис линейного пространства
Размерностью линейного пространства называется величина равная наибольшему числу имеющемуся в нем линейно независимых векторов. Например, на прямой существует один линейно независимый вектор, а любые два вектора – линейно зависимы. Следовательно, прямая представляет одномерное пространство - R1. На плоскости существуют два линейно независимых вектора, а любые три – линейно зависимы. Следовательно плоскость является двухмерным пространством R2. В пространстве существует три линейно независимых вектора. Поэтому размерность пространства равна трем – R3.
В линейном пространстве размерности n-Rn должны существовать n независимых векторов 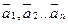 , а любые n+1 векторов должны быть линейно зависимы. Выберем в этом пространстве еще один вектор
, а любые n+1 векторов должны быть линейно зависимы. Выберем в этом пространстве еще один вектор 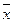 , тогда совокупность векторов
, тогда совокупность векторов 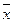 ,
, 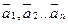 - линейно зависима, так как их число равно n+1>n. Поэтому найдется такой набор чисел λ1,λ2,…λn, что
- линейно зависима, так как их число равно n+1>n. Поэтому найдется такой набор чисел λ1,λ2,…λn, что 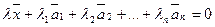 . При этом λ≠0 т.к. в противном случае вектора
. При этом λ≠0 т.к. в противном случае вектора 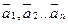 - линейно зависимы. Отсюда вектор
- линейно зависимы. Отсюда вектор 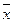 может быть представлен в виде линейной комбинации векторов
может быть представлен в виде линейной комбинации векторов 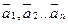 .
. 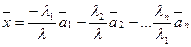 . Предположим, теперь, что
. Предположим, теперь, что 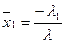 ;
; 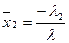 ;
; 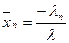 , тогда
, тогда 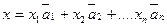 (1). Докажем теперь единственность такого разложения методом отпротивного. Пусть существует другое разложение вектора
(1). Докажем теперь единственность такого разложения методом отпротивного. Пусть существует другое разложение вектора 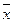 по векторам
по векторам 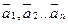 т.е.
т.е. 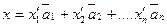 . Тогда
. Тогда 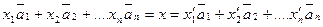 или
или 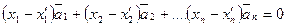 , но
, но 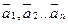 по условию линейно независимы, поэтому для выполнения равенства необходимо чтобы
по условию линейно независимы, поэтому для выполнения равенства необходимо чтобы 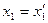 ;
; 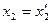 ;
; 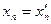 . Следовательно мы доказали, что любой вектор может быть, и притом единственный образом, представлен в виде линейной комбинации линейно независимых векторов (
. Следовательно мы доказали, что любой вектор может быть, и притом единственный образом, представлен в виде линейной комбинации линейно независимых векторов ( 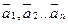 ). Совокупность таких векторов и называется базисом n-мерного линейного пространства, а числа (
). Совокупность таких векторов и называется базисом n-мерного линейного пространства, а числа ( 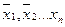 ) – координаты вектора
) – координаты вектора 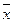 в этом базисе. Число этих векторов равно рангу системы. Так в R1любой вектор
в этом базисе. Число этих векторов равно рангу системы. Так в R1любой вектор 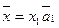 . На плоскости R2
. На плоскости R2 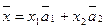 , где
, где 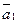 и
и 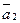 - неколлинеарные вектора этой плоскости. И, наконец, в пространстве
- неколлинеарные вектора этой плоскости. И, наконец, в пространстве 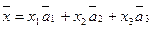 , где
, где 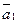 ,
, 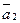 и
и 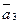 - три некомпланарных вектора пространства.
- три некомпланарных вектора пространства.
Разложение (1) можно более коротко записать в виде 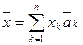 или просто
или просто 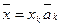 - в соответствии с правилом получившем название «соглашение о суммировании» - предложенном А.Эйнштейном. Индекс k называется индексом суммирования.
- в соответствии с правилом получившем название «соглашение о суммировании» - предложенном А.Эйнштейном. Индекс k называется индексом суммирования.
Следует отметить, что при заданном базисе векторы пространств R1, R2, R3- определяются своими координатами, т.е. эти пространства могут быть рассмотрены как частные виды пространства Rn при n=1,2,3.
3.3. Разложение вектора в ортогональном базисе.
Рассмотрим базис пространства Rn, в котором каждый вектор ортогонален остальным векторам базиса. 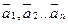 ;
; 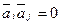 - по условию ортогональности при i≠j,
- по условию ортогональности при i≠j, 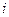 ,j=(1,2,…n).
,j=(1,2,…n).
Ортогональные базисы удобны потому, что координаты разложения произвольного вектора определяются очень просто без трудоемких вычислений .
Действительно, разложим произвольный вектор 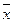 в ортогональном базисе. Составим разложение этого вектора с неизвестными пока координатами в данном базисе:
в ортогональном базисе. Составим разложение этого вектора с неизвестными пока координатами в данном базисе:
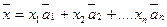 (1)
(1)
умножим обе части этого равенства, представляющие собой вектора, на вектор 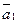 .
.
В силу свойств скалярного произведения векторов, получим:
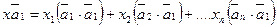
Однако, в силу взаимной ортогональности векторов базиса, все скалярные произведения векторов базиса, за исключением первого, равны нулю, т.е. коэффициент x1 будет определятся по формуле 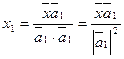
Умножая поочередно (1) на другие базисные векторы получим общую формулу для коэффициентов разложения вектора 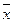 .
.
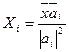 ;
; 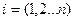
Частным случаем ортогонального базиса является случай, когда все векторы 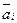 имеют единичную длину |
имеют единичную длину | 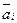 |=1 ; в таком случае базис называют нормированным и координаты разложения имеют наиболее простой вид:
|=1 ; в таком случае базис называют нормированным и координаты разложения имеют наиболее простой вид:
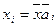 i=1,2,….n
i=1,2,….n
Переход к новому базису.
Пусть B=( 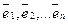 ) и B'=(
) и B'=( 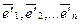 ) старый и новый базисы линейного векторного пространства Rn. Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
) старый и новый базисы линейного векторного пространства Rn. Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
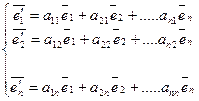
Или
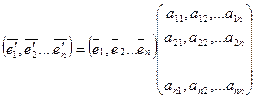
Или в сокращенной матричной форме:
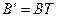 ,где
,где 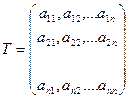
T - называется матрицей перехода от старого базиса 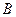 к новому
к новому 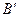 .Следует обратить внимание на то, что координаты разложения нового базиса по старому базису располагаются в матрице перехода по столбцам. Матрица перехода от нового базиса к старому имеет вид:
.Следует обратить внимание на то, что координаты разложения нового базиса по старому базису располагаются в матрице перехода по столбцам. Матрица перехода от нового базиса к старому имеет вид:
T-1; B =B′ ·T-1;
Найдем зависимость между координатами вектора в разных базисах. Пусть некоторый вектор 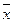 имеет координаты (x1 x2 …хn) в старом и (x'1, x'2,...x'n) в новом, тогда
имеет координаты (x1 x2 …хn) в старом и (x'1, x'2,...x'n) в новом, тогда
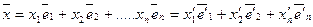
Подставив сюда разложение векторов ( 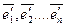 ) по базису(
) по базису( 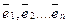 ),получим:
),получим:
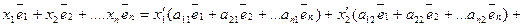
+ 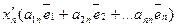

Перенесем все влево и сгруппируем слагаемые с одинаковыми сомножителями 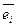
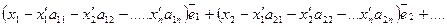
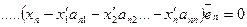
Это равенство выполняется при условии, что все коэффициенты перед 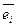 равны 0. следовательно:
равны 0. следовательно:
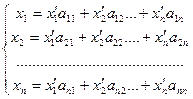
Или в матричной форме:
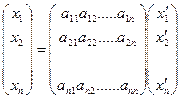 или X=TX1
или X=TX1
Линейные операторы.
Пусть Rn1 Rm2-линейные пространства размерности nи m. Если задан закон (правило),по которому каждому вектору x пространства Rn1 ставится в соответствии единственный вектор y пространства Rm2, то говорят, что задан оператор 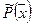 действующий из Rn1 в Rm2 и записывают эту операцию
действующий из Rn1 в Rm2 и записывают эту операцию 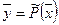 . Оператор называется линейным, если для любых векторов xи yпространства Rnи любого числа λ выполняются соотношения:
. Оператор называется линейным, если для любых векторов xи yпространства Rnи любого числа λ выполняются соотношения:
1) 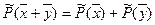
2) 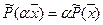
Вектор 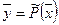 -называется образом вектора
-называется образом вектора 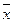 ,а сам вектор
,а сам вектор 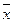 –прообразом вектора
–прообразом вектора 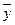 .
.
Если пространства Rn1 и R m 2 совпадают, то оператор 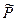 отображает пространство Rn1 в себя. Именно такие операторы мы и будем рассматривать.
отображает пространство Rn1 в себя. Именно такие операторы мы и будем рассматривать.
Пусть в пространстве Rn задан базис( 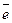 1,
1, 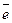 2,..
2,.. 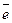 n).Произвольный вектор
n).Произвольный вектор 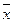 может быть разложен по этому базису:
может быть разложен по этому базису:
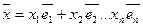
Выясним, что собой представляет оператор 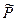 , для этого подействуем на вектор
, для этого подействуем на вектор 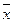 оператором
оператором 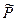 :
:
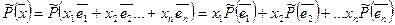
Поскольку 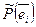 (i=1,2..n) является вектором Rn то их также можно разложить по базису (
(i=1,2..n) является вектором Rn то их также можно разложить по базису ( 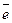 1,
1, 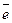 2,..
2,.. 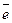 n):
n):
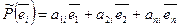 и тогда
и тогда
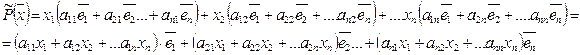 (1)
(1)
С дpугой стороны 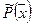 по определению, есть некоторый вектор
по определению, есть некоторый вектор 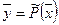 , и имеет в том же базисе (
, и имеет в том же базисе ( 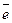 1,
1, 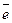 2,..
2,.. 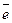 n), координаты y1,y2...yn и поэтому он может быть разложен по этому базису:
n), координаты y1,y2...yn и поэтому он может быть разложен по этому базису:
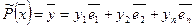 (2)
(2)
Разложение вектора 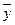 по базису единственно, поэтому правые части (1) и (2) равны следовательно:
по базису единственно, поэтому правые части (1) и (2) равны следовательно:
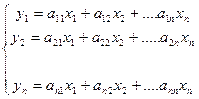
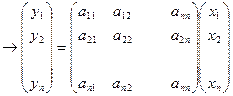
Или в матричной форме 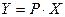
Таким образом, действие линейного оператора на вектор 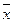 сводится к умножению некоторой матрицы P=(
сводится к умножению некоторой матрицы P=(  ij) на матрицу столбец, составленный из координат вектора
ij) на матрицу столбец, составленный из координат вектора 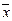 . Матрица P называется матрицей линейного оператора
. Матрица P называется матрицей линейного оператора 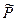 в базисе (
в базисе ( 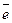 1,
1, 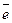 2,..
2,.. 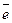 n), а ранг матрицы рангом оператора
n), а ранг матрицы рангом оператора 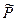 . Таким образом, каждому линейному оператору соответствует матрица в данном базисе и наоборот.
. Таким образом, каждому линейному оператору соответствует матрица в данном базисе и наоборот.
Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой .
Теорема1. матрицы P и P' линейного оператора 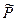 ,в старом базисе (
,в старом базисе ( 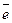 1,
1, 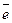 2,..
2,.. 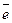 n) и новом
n) и новом 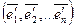 связаны соотношениями:
связаны соотношениями:
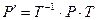 , где Т – матрица перехода от старого базиса к новому.
, где Т – матрица перехода от старого базиса к новому.
Теорема2. Определитель матрицы линейного оператора не зависит от выбора базиса.
