Линейные пространства. Подпространства. Размерность и базис
Подмножество линейного пространства образует подпространство, если оно замкнуто относительно сложения векторов и умножения на скаляры.
П р и м е р 6.1. Образует ли подпространство в плоскости множество векторов, концы которых лежат: а) в первой четверти; б) на прямой, проходящей через начало координат? (начала векторов лежат в начале координат)
Р е ш е н и е.
а) нет, так как множество не замкнуто относительно умножения на скаляр: при умножении на отрицательное число конец вектора попадает в третью четверть.
б) да, так как при сложении векторов и умножении их на любое число их концы остаются на той же прямой.
У п р а ж н е н и е 6.1. Образуют ли подпространство следующие подмножества соответствующих линейных пространств:
а) множество векторов плоскости, концы которых лежат в первой или третьей четверти;
б) множество векторов плоскости, концы которых лежат на прямой, не проходящей через начало координат;
в) множество координатных строк {(x1, x2, x3)ï x1 + x2 + x3 = 0};
г) множество координатных строк {(x1, x2, x3)ï x1 + x2 + x3 = 1};
д) множество координатных строк {(x1, x2, x3)ï x1 = x2 2}.
Размерностью линейного пространства L называется число dim L векторов, входящих в любой его базис.
Размерность суммы и пересечения подпространств связаны соотношением
dim (U + V) = dim U + dim V – dim (U Ç V).
П р и м е р 6.2. Найти базис и размерность суммы и пересечения подпространств, натянутых на следующие системы векторов:
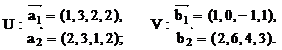
Р е ш е н и е. Каждая из систем векторов, порождающих подпространства U и V, линейно независима, значит, является базисом соответствующего подпространства. Построим матрицу из координат данных векторов, расположив их по столбцам и отделив чертой одну систему от другой. Приведем получившуюся матрицу к ступенчатому виду.

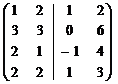 ~
~ 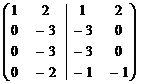 ~
~ 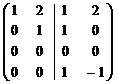 ~
~ 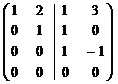 .
.
Базис U + V образуют векторы 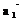 ,
, 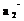 ,
, 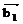 , которым в ступенчатой матрице соответствуют ведущие элементы. Следовательно, dim (U + V) = 3. Тогда
, которым в ступенчатой матрице соответствуют ведущие элементы. Следовательно, dim (U + V) = 3. Тогда
dim (UÇV) = dim U + dim V – dim (U + V) = 2 + 2 – 3 = 1.
Пересечение подпространств образует множество векторов, удовлетворяющих уравнению 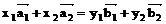 (стоящих в левой и правой частях этого уравнения). Базис пересечения получим с помощью фундаментальной системы решений системы линейных уравнений, соответствующей этому векторному уравнению. Матрица этой системы уже приведена к ступенчатому виду. Исходя из него, заключаем, что y2 – свободная переменная, и полагаем y2 = c. Тогда 0 = y1 – y2, y1 = c,. и пересечение подпространств образует множество векторов вида
(стоящих в левой и правой частях этого уравнения). Базис пересечения получим с помощью фундаментальной системы решений системы линейных уравнений, соответствующей этому векторному уравнению. Матрица этой системы уже приведена к ступенчатому виду. Исходя из него, заключаем, что y2 – свободная переменная, и полагаем y2 = c. Тогда 0 = y1 – y2, y1 = c,. и пересечение подпространств образует множество векторов вида 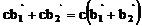 = с (3, 6, 3, 4). Следовательно, базис UÇV образует вектор (3, 6, 3, 4).
= с (3, 6, 3, 4). Следовательно, базис UÇV образует вектор (3, 6, 3, 4).
З а м е ч а н и я. 1. Если продолжить решать систему, находя значения переменных х, то получим x2 = c, x1 = c, и в левой части векторного уравнения получится вектор 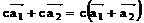 , равный полученному выше.
, равный полученному выше.
2. Указанным методом можно получить базис суммы независимо от того, являются ли порождающие системы векторов линейно независимыми. Но базис пересечения будет получен правильно, только если хотя бы система, порождающая второе подпространство, линейно независима.
3. Если будет установлено, что размерность пересечения равна 0, то пересечение не имеет базиса, и искать его не нужно.
У п р а ж н е н и е 6.2. Найти базис и размерность суммы и пересечения подпространств, натянутых на следующие системы векторов:
а) 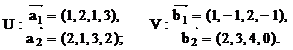
б) 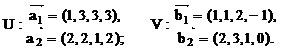
Евклидово пространство
Евклидовым пространством называется линейное пространство над полем R, в котором определено скалярное умножение, ставящее в соответствие каждой паре векторов 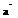 ,
, 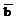 скаляр
скаляр 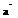
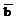 , причем выполнены условия:
, причем выполнены условия:
1) 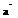
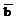 =
= 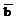
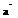 ;
;
2) (a 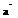 + b
+ b 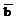 )
) 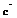 = a(
= a( 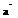
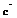 ) + b(
) + b( 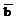
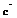 );
);
3) 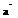 ¹
¹ 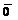 Þ
Þ 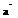
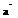 > 0.
> 0.
Стандартное скалярное произведение вычисляется по формулам
(a1 , … , an) (b1, … , bn) = a1b1 + … + anbn.
Векторы 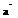 и
и 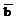 называются ортогональными, записывается
называются ортогональными, записывается 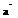 ^
^ 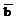 , если их скалярное произведение равно 0.
, если их скалярное произведение равно 0.
Система векторов называется ортогональной, если векторы в ней попарно ортогональны.
Ортогональная система векторов линейно независима.
Процесс ортогонализации системы векторов 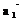 , … ,
, … , 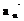 заключается в переходе к эквивалентной ортогональной системе
заключается в переходе к эквивалентной ортогональной системе 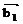 , … ,
, … , 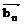 , выполняемом по формулам:
, выполняемом по формулам:
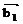 =
= 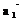 ;
;
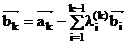 , где
, где 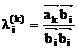 , k = 2, … , n.
, k = 2, … , n.
П р и м е р 7.1. Ортогонализировать систему векторов
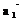 = (1, 2, 2, 1),
= (1, 2, 2, 1), 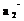 = (3, 2, 1, 1),
= (3, 2, 1, 1), 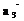 = (4, 1, 3, -2).
= (4, 1, 3, -2).
Р е ш е н и е. Имеем 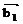 =
= 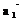 = (1, 2, 2, 1);
= (1, 2, 2, 1);
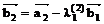 ,
, 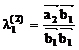 =
= 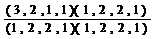 =
= 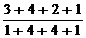 = 1;
= 1;
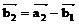 = (3, 2, 1, 1) – (1, 2, 2, 1) = (2, 0, -1, 0).
= (3, 2, 1, 1) – (1, 2, 2, 1) = (2, 0, -1, 0).
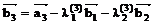 ,
, 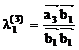 =
= 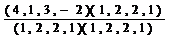 =
= 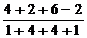 =1;
=1;
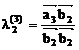 =
= 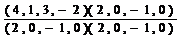 =1;
=1;
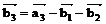 = (4, 1, 3, -2) – (1, 2, 2, 1) – (2, 0, -1, 0) = (1, -1, 2, -3).
= (4, 1, 3, -2) – (1, 2, 2, 1) – (2, 0, -1, 0) = (1, -1, 2, -3).
У п р а ж н е н и е 7.1. Ортогонализировать системы векторов:
а) 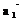 = (1, 1, 0, 2),
= (1, 1, 0, 2), 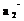 = (3, 1, 1, 1),
= (3, 1, 1, 1), 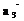 = (-1, -3, 1, -1);
= (-1, -3, 1, -1);
б) 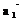 = (1, 2, 1, 1),
= (1, 2, 1, 1), 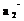 = (3, 4, 1, 1),
= (3, 4, 1, 1), 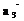 = (0, 3, 2, -1).
= (0, 3, 2, -1).
П р и м е р 7.2. Дополнить систему векторов 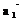 = (1, -1, 1, -1),
= (1, -1, 1, -1),
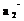 = (1, 1, -1, -1), до ортогонального базиса пространства.
= (1, 1, -1, -1), до ортогонального базиса пространства.
Р е ш е н и е. Исходная система ортогональна, поэтому задача имеет смысл. Так как векторы заданы в четырехмерном пространстве, то требуется найти еще два вектора. Третий вектор 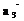 = (x1, x2, x3, x4) определяем из условий
= (x1, x2, x3, x4) определяем из условий 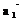
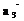 = 0,
= 0, 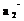
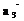 = 0. Эти условия дают систему уравнений, матрица которой образована из координатных строк векторов
= 0. Эти условия дают систему уравнений, матрица которой образована из координатных строк векторов 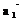 и
и 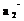 . Решаем систему:
. Решаем систему:
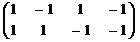 ~
~ 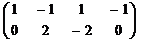 ~
~ 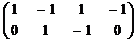 .
.
Свободным переменным x3 и x4 можно придать любой набор значений, отличный от нулевого. Полагаем, например, x3 = 0, x4 = 1. Тогда x2 = 0, x1 = 1, и 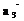 = (1, 0, 0, 1).
= (1, 0, 0, 1).
Аналогично находим 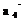 = (y1, y2, y3, y4). Для этого к полученной выше ступенчатой матрице добавляем новую координатную строку и приводим к ступенчатому виду:
= (y1, y2, y3, y4). Для этого к полученной выше ступенчатой матрице добавляем новую координатную строку и приводим к ступенчатому виду:
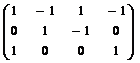 ~
~ 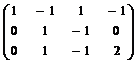 ~
~ 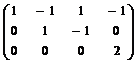 .
.
Для свободной переменной y3 полагаем y3 = 1. Тогда y4 = 0, y2 = 1, y1= 0, и 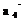 = (0, 1, 1, 0).
= (0, 1, 1, 0).
Нормой вектора 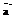 евклидова пространства называется неотрицательное действительное число
евклидова пространства называется неотрицательное действительное число 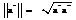 .
.
Вектор называется нормированным, если его норма равна 1.
Чтобы нормировать вектор, его следует разделить на его норму.
Ортогональная система нормированных векторов называется ортонормированной.
У п р а ж н е н и е 7.2. Дополнить систему векторов до ортонормированного базиса пространства:
а) 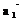 = (1/2, 1/2, 1/2, 1/2),
= (1/2, 1/2, 1/2, 1/2), 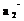 = (-1/2, 1/2, -1/2, 1/2);
= (-1/2, 1/2, -1/2, 1/2);
б) 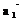 = (1/3, -2/3, 2/3).
= (1/3, -2/3, 2/3).
Линейные отображения
Пусть U и V – линейные пространства над полем F. Отображение f: U ® V называется линейным, если 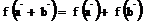 и
и 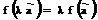 .
.
П р и м е р 8.1. Являются ли линейными преобразования трехмерного пространства:
а) f(x1, x2, x3) = (2x1, x1 – x3, 0);
б) f(x1, x2, x3) = (1, x1 + x2, x3).
Р е ш е н и е.
а) Имеем f((x1, x2, x3) + (y1, y2, y3)) = f(x1 + y1, x2 + y2, x3 + y3) =
= (2(x1 + y1), (x1 + y1) – (x3 + y3), 0) = (2x1, x1 – x3 , 0) + (2y1, y1 - y3, 0) =
= f((x1, x2, x3) + f(y1, y2, y3));
f(l(x1, x2, x3)) = f(lx1, lx2, lx3) = (2lx1, lx1 – lx3, 0) = l(2x1, x1 – x3, 0) =
= l f(x1, x2, x3).
Следовательно, преобразование является линейным.
б) Имеем f((x1, x2, x3) + (y1, y2, y3)) = f(x1 + y1, x2 + y2, x3 + y3) =
= (1, (x1 + y1) + (x2 + y2), x3 + y3);
f((x1, x2, x3) + f(y1, y2, y3)) = (1, x1 + x2, x3) + (1, y1 + y2, y3) =
= (2, (x1 + y1) + (x2 + y2), x3 + y3) ¹ f((x1, x2, x3) + (y1, y2, y3)).
Следовательно, преобразование не является линейным.
Образом линейного отображения f: U ® V называется множество образов векторов из U, то есть
Im (f) = {f( 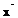 ) ï
) ï 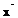 Î U}.
Î U}.
Ядром линейного отображения f: U ® V называется множество векторов из U, отображающихся в 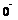 , то есть
, то есть
Ker (f) = { 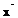 Î Uï f(
Î Uï f( 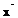 ) =
) = 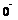 }.
}.
Im (f) и Ker (f) являются подпространствами в пространствах V и U соответственно. Их размерности называются рангом и дефектом линейного отображения f и обозначаются rank f и def f соответственно.
Ранг и дефект линейного отображения f: U ® V связаны соотношением
rank f + def f = dim U.
Пусть задано линейное отображение f: U ® V, и 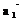 , … ,
, … , 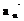 ;
; 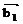 , … ,
, … , 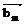 – базисы пространств U и V соответственно. Пусть
– базисы пространств U и V соответственно. Пусть
f( 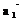 ) = a11
) = a11 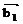 + … + am1
+ … + am1 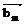 ;
;
………………………………
f( 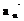 ) = a1n
) = a1n 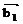 + … + anm
+ … + anm 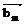 .
.
Матрицей линейного отображения f называется матрица
A = 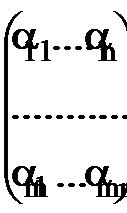 .
.
Образ любого вектора 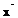 можно найти с помощью матричного умножения: f(
можно найти с помощью матричного умножения: f( 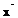 ) = А
) = А 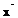 , где
, где 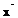 записан в виде столбца.
записан в виде столбца.
П р и м е р 8.2. Найти ранг, дефект, базисы образа и ядра линейного отображения f, заданного матрицей
А = 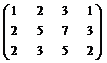 .
.
Р е ш е н и е. Образ отображения порождается образами базисных векторов, расположенных по столбцам матрицы А. Поэтому базис образа – это базис системы столбцов. Находим его приведением матрицы к ступенчатому виду:
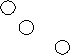
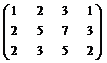 ~
~ 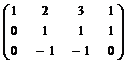 ~
~ 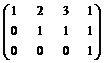 .
.
Заключаем, что базис Im f образуют векторы (1, 2, 2), (2, 5, 3) и (1, 3, 2). Следовательно, rank f = 3. Исходное пространство имеет размерность 4 (число столбцов матрицы), поэтому def f = 4 – rank f = 1.
Ядро отображения – это множество решений уравнения А 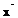 =
= 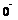 , базис ядра – фундаментальная система решений соответствующей системы линейных уравнений. Матрица системы уже приведена к ступенчатому виду. Полагаем
, базис ядра – фундаментальная система решений соответствующей системы линейных уравнений. Матрица системы уже приведена к ступенчатому виду. Полагаем
x3 = a, тогда x4 = 0, x2 = -a, x1 = -a, 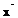 = (-a, -a, a, 0) = a(-1, -1, 1, 0). Таким образом, базис ядра образует вектор (-1, -1, 1, 0).
= (-a, -a, a, 0) = a(-1, -1, 1, 0). Таким образом, базис ядра образует вектор (-1, -1, 1, 0).
З а м е ч а н и е. Если будет получено, что def f = 0, то ядро будет нулевым пространством и не имеет базиса.
У п р а ж н е н и е 8.1. Найти ранг, дефект, базисы образа и ядра линейного отображения f, заданного матрицей:
а) А = 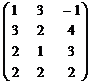 ; б) А =
; б) А = 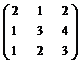 ; в) А =
; в) А = 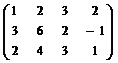 .
.
