Метод интегрирования по частям
Пусть функции 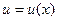 и
и 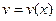 имеют непрерывные производные на некотором промежутке. Найдем дифференциал произведения этих функций:
имеют непрерывные производные на некотором промежутке. Найдем дифференциал произведения этих функций:
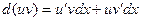 .
.
Так как по условию функции 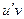 и
и 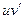 непрерывны, можно проинтегрировать обе части этого равенства,
непрерывны, можно проинтегрировать обе части этого равенства,
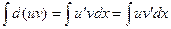 ,
,
или
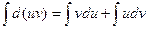
но
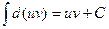 ,
,
следовательно
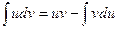 (4)
(4)
В правой части формулы (4) постоянную интегрирования С не пишут, т.к она фактически присутствует в интеграле 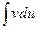 . Формула (4) называется формулой интегрирования по частям.
. Формула (4) называется формулой интегрирования по частям.
Сущность метода интегрирования по частям вполне соответствует его названию. Дело в том, что при вычислении интеграла этим методом подынтегральное выражение 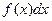 представляется в виде произведения множителей
представляется в виде произведения множителей 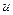 и
и 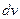 ; при этом
; при этом 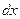 обязательно входят в
обязательно входят в 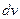 . В результате получается, что заданный интеграл находят по частям: сначала находят
. В результате получается, что заданный интеграл находят по частям: сначала находят 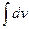 , а затем
, а затем 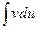 . Естественно, что этот метод применим лишь в случае, если задача нахождения указанных двух интегралов более проста, чем нахождение заданного интеграла.
. Естественно, что этот метод применим лишь в случае, если задача нахождения указанных двух интегралов более проста, чем нахождение заданного интеграла.
При вычислении интегралов методом интегрирования по частям главным является разумное разбиение подынтегрального выражения на множители 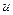 и
и 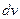 . Общих установок по этому вопросу не имеется. Однако, для некоторых типов интегралов, вычисляемых методом интегрирования по частям, сделать это возможно.
. Общих установок по этому вопросу не имеется. Однако, для некоторых типов интегралов, вычисляемых методом интегрирования по частям, сделать это возможно.
1. В интегралах вида: 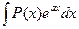 ,
, 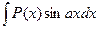 ,
, 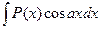 ,
,
где Р(х) – многочлен относительно х, а – некоторое число, полагают 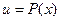 , а все
, а все
остальные сомножители за 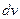 .
.
2. В интегралах вида: 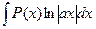 ,
, 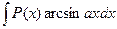 ,
, 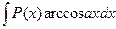 ,
,
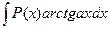 ,
, 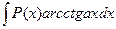
полагают 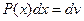 , а остальные сомножители за
, а остальные сомножители за 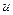 .
.
3. В интегралах вида: 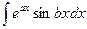 ,
, 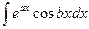 , где a и b числа, за
, где a и b числа, за 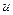 можно принять
можно принять
любую из функций 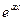 или sin bx (или cos bx).
или sin bx (или cos bx).
Пример по выполнению практической работы
Пример 1.Вычислить: 1) 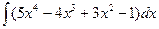 ; 2)
; 2) 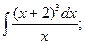
Решение:
1) 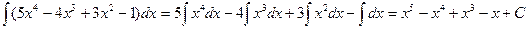 ;
;
2) 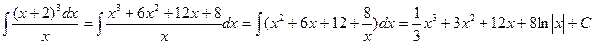
Пример 2.Вычислить 1) 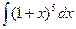 ; 2)
; 2)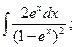 3)
3) 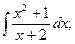 4)
4) 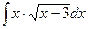 ;
;
5) 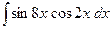 ;
;
Решение:
1) Положим 1+x = z. Продифференцируем это неравенство: d(1+ x)= dz или dx = dz. Заменим в интеграле: 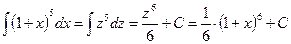 .
.
2)Сделав замену: 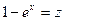 , получим
, получим 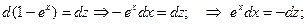
Тогда:
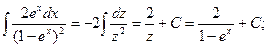
3) Положим 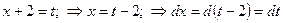
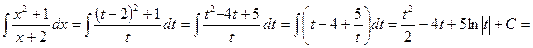
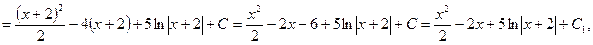
где 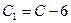 ;
;
4) Пусть 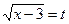 , тогда
, тогда 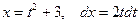 . Поэтому
. Поэтому

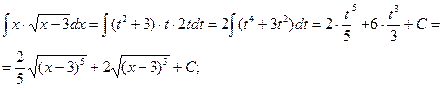
5) Этот интеграл решается с помощью формул тригонометрии:
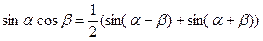 .
.
Поэтому, имеем 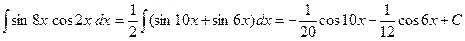 ;
;
Пример 3.Вычислить 1) 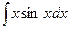 ; 2)
; 2) 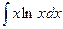 ;
;
Решение:
1) положим 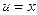 ,
, 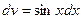 ; тогда
; тогда 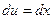 ,
, 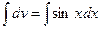 , т.е.
, т.е. 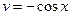 . Используя формулу (4), получим
. Используя формулу (4), получим 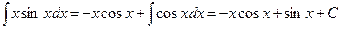 .
.
2) 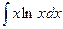 ; положим u=lnx, dv=xdx; тогда
; положим u=lnx, dv=xdx; тогда 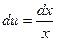 ;
; 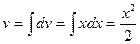 .
.
Задания для практического занятия:
Вариант 1
1. Методом непосредственного интегрирования вычислить:
а) 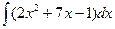 ; б)
; б) 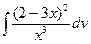 в)
в) 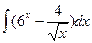
г) 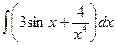 ; д)
; д) 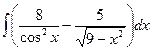 ; е)
; е) 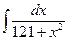 ;
;
2. Методом подстановки вычислить:
а) 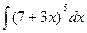 ; б)
; б) 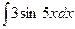 ; в)
; в) 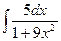 ; г)
; г) 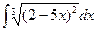 ;
;
д) 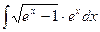 е)
е) 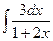 ; ж)
; ж) 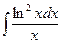 ; з)
; з) 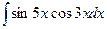 ;
;
3. Методом интегрирования по частям вычислить:
а) 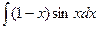 б)
б) 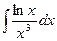
Вариант 2
1. Методом непосредственного интегрирования вычислить:
а) 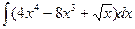 ; б)
; б) 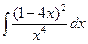 ; в)
; в) 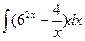 ;
;
г) 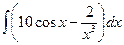 ; д)
; д) 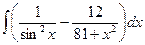 ; е)
; е) 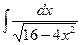 ;
;
2. Методом подстановки вычислить:
а) 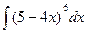 ; б)
; б) 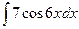 ; в)
; в) 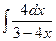 ; г)
; г) 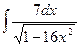 ;
;
д) 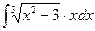 ; е)
; е) 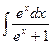 ; ж)
; ж) 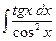 ; з)
; з) 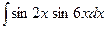 ;
;
3. Методом интегрирования по частям вычислить:
а) 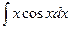 ; б)
; б) 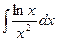
Вариант 3
1. Методом непосредственного интегрирования вычислить:
а) 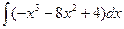 ; б)
; б) 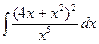 ; в)
; в) 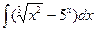
г) 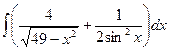 ; д)
; д) 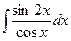 ; е)
; е) 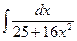 ;
;
2. Методом подстановки вычислить:
а) 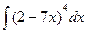 ; б)
; б) 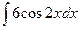 ; в)
; в) 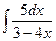 ; г)
; г) 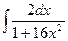 ;
;
д) 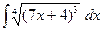 ; е)
; е) 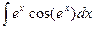 ; ж)
; ж) 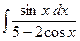 ; з)
; з) 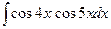 ;
;
3. Методом интегрирования по частям вычислить:
а) 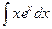 ; б)
; б) 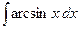 ;
;
Вариант 4
1. Методом непосредственного интегрирования вычислить:
а) 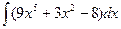 ; б)
; б) 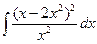 ; в)
; в) 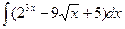 ;
;
г) 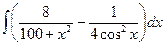 ; д)
; д) 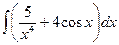 ; е)
; е) 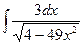 .
.
2. Методом подстановки вычислить:
а) 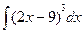 ; б)
; б) 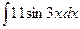 ; в)
; в) 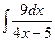 ; г)
; г)  ;
;
д) 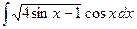 ; е)
; е) 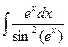 ; ж)
; ж) 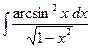 ; з)
; з) 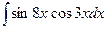 ;
;
3. Методом интегрирования по частям вычислить:
а) 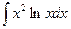 ; б)
; б) 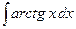 .
.
Контрольные вопросы
1. Какая функция называется первообразной для функции 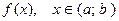 ?
?
2. Что называется неопределенным интегралом функции 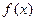 на некотором промежутке?
на некотором промежутке?
3. Перечислите основные свойства неопределенного интеграла.
4. Перечислите основные табличные интегралы.
5. Какие методы интегрирования вы знаете?
Практическая работа № 23
«Вычисление определенных интегралов»
Цель работы:научиться вычислять определенные интегралы.
Образовательные результаты, заявленные во ФГОС:
Студент должен
уметь:
- применять методы дифференциального и интегрального исчисления.
знать:
- основы дифференциального и интегрального исчисления.
Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.
Методические указания по выполнению работы:
1. Ознакомиться с теоретическим материалом по практической работе.
2. Рассмотрите образцы решения задач по теме.
3.Выполнить предложенное задание согласно варианту по списку группы.
4.Изучить условие заданий для практической работы и выполнить её.
5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.
5. Оформить отчет о работе. Сделайте вывод.
