Производные и дифференциалы высших порядков
Производная 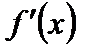 функции
функции 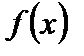 , очевидно, зависит от x, т.е.
, очевидно, зависит от x, т.е. 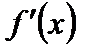 есть также функция аргумента x и по отношению к ней также можно ставить вопрос о производной. Производная от
есть также функция аргумента x и по отношению к ней также можно ставить вопрос о производной. Производная от 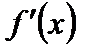 , т.е. производная от производной, называется второй производной и обозначается
, т.е. производная от производной, называется второй производной и обозначается 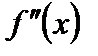 :
:
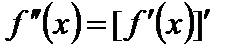 .
.
Часто вместо 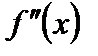 применяют символ
применяют символ 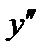 :
:
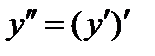 .
.
Аналогично определяется третья производная, или производная третьего порядка– как производная от второй производной: 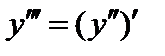 и т.д. Таким образом, производная n-го порядка определяется как производная от производной (n – 1)-го порядка:
и т.д. Таким образом, производная n-го порядка определяется как производная от производной (n – 1)-го порядка:
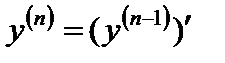 .
.
Рассмотрим примеры:
1) 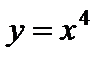 .
.
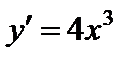 ,
, 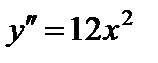 ;
;
2) 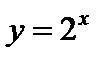 .
.
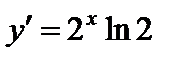 ,
, 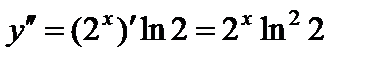
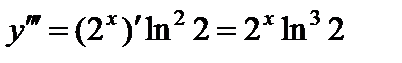 ;
;
3) 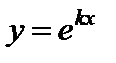 .
.
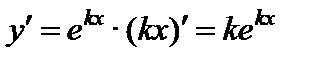 ,
, 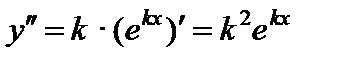 ,
,
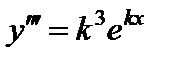 , ...,
, ..., 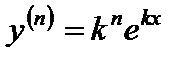 ;
;
4) 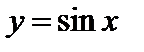 .
.
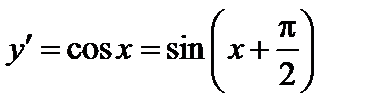 ,
, 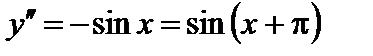 ,
,
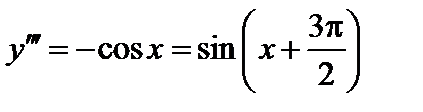 , ...,
, ..., 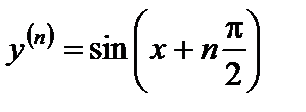 .
.
Аналогичным образом определяются дифференциалы второго, третьего и более высоких порядков:
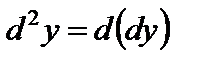 ,
, 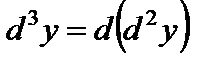 , ...
, ...
Можно показать, что
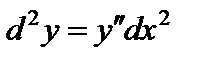 ,
, 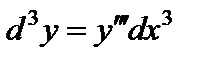 , ... .
, ... .
Лекция 4. Применение производных
в исследовании функций
4.1. Основные теоремы дифференциального
исчисления
1. Теорема Ферма.Пусть функция 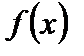 определена на интервале
определена на интервале 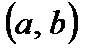 и имеет наибольшее (наименьшее) значение в точке
и имеет наибольшее (наименьшее) значение в точке 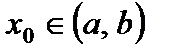 . Тогда если в точке
. Тогда если в точке 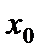 существует производная этой функции, она равна нулю:
существует производная этой функции, она равна нулю:
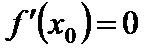 .
.
Доказательство. Докажем теорему для случая, когда функция имеет в точке 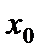 наибольшее значение (для наименьшего значения доказательство аналогично). В этом случае для всех
наибольшее значение (для наименьшего значения доказательство аналогично). В этом случае для всех 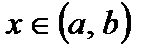 выполняется неравенство
выполняется неравенство 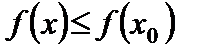 , что означает
, что означает
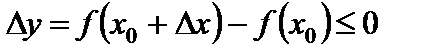
для любой точки 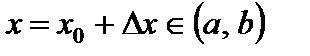 .
.
Если 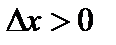 , то
, то
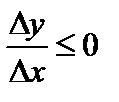 . (1)
. (1)
Если 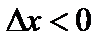 , то
, то
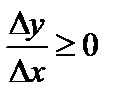 . (2)
. (2)
Но из условия теоремы производная в точке 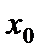 существует, тогда, переходя к пределу при
существует, тогда, переходя к пределу при 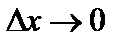 , получаем
, получаем
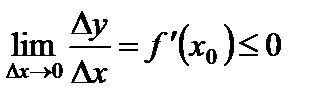 при
при 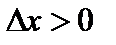 ,
,
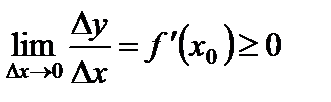 при
при 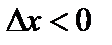 .
.
Но соотношения 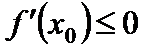 ,
, 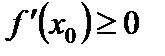 совместимы лишь в том случае, если
совместимы лишь в том случае, если 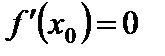 .
.
Теорема доказана.
Геометрический смысл теоремы Ферма заключается в том, что если дифференцируемая функция в точке 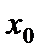 принимает наибольшее (наименьшее) значение, то касательная к графику этой функции в точке
принимает наибольшее (наименьшее) значение, то касательная к графику этой функции в точке 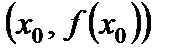 параллельна оси Ox (см. рис. 1).
параллельна оси Ox (см. рис. 1).
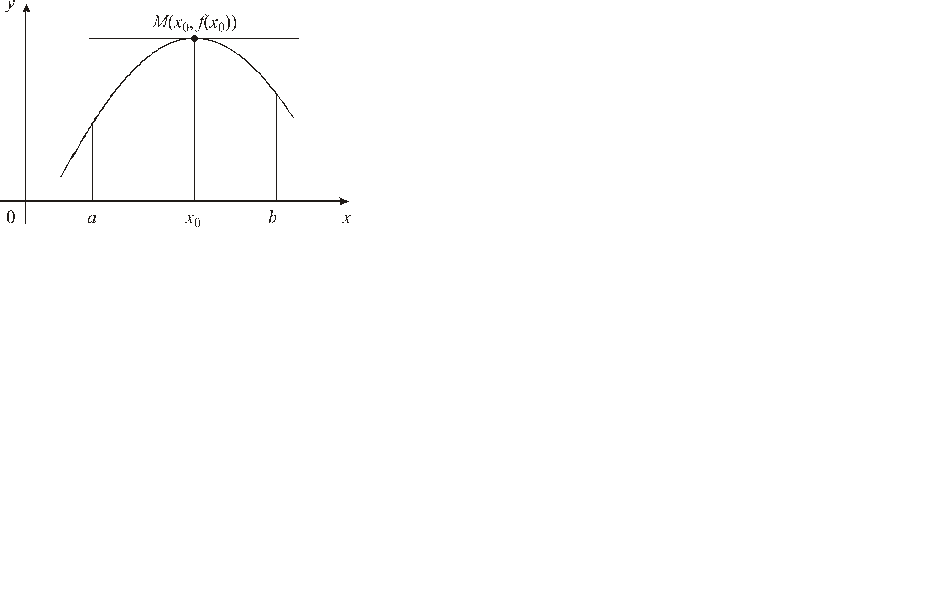 |
| Рис. 1 |
2. Теорема Ролля. Пусть функция 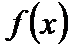 удовлетворяет следующим трем условиям:
удовлетворяет следующим трем условиям:
1) непрерывна на отрезке 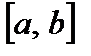 ;
;
2) дифференцируема на интервале 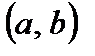 ;
;
3) на концах отрезка принимает равные значения: 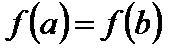 .
.
Тогда внутри отрезка существует хотя бы одна точка 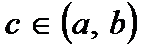 , в которой производная функции равна нулю:
, в которой производная функции равна нулю:
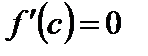 .
.
Доказательство. Известно (см. п. 2.5), что функция, непрерывная на отрезке, достигает на нем своего наибольшего значения M и своего наименьшего значения m. Если оба эти значения достигаются на концах отрезка, то по условию 3) они равны: 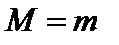 , т.е.
, т.е. 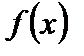 есть константа. В этом случае производная равна нулю во всех точках отрезка.
есть константа. В этом случае производная равна нулю во всех точках отрезка.
Если же 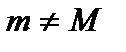 , то хотя бы одно из этих значений достигается внутри отрезка, в некоторой точке
, то хотя бы одно из этих значений достигается внутри отрезка, в некоторой точке 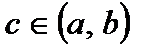 . Тогда по теореме Ферма
. Тогда по теореме Ферма 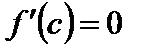 .
.
Доказательство закончено.
3. Теорема Лагранжа. Пусть функция 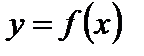 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) непрерывна на отрезке 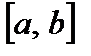 ;
;
2) дифференцируема на интервале 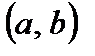 .
.
Тогда внутри отрезка существует такая точка 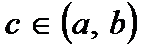 , что справедлива формула
, что справедлива формула
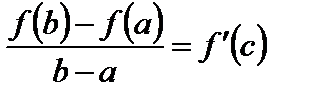 . (3)
. (3)
Доказательство. Возьмем вспомогательную функцию
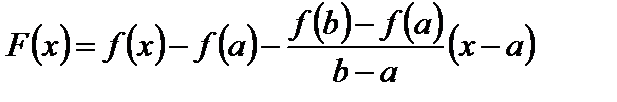 . (4)
. (4)
Эта функция 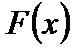 удовлетворяет всем трем условиям теоремы Ролля: она непрерывна на отрезке
удовлетворяет всем трем условиям теоремы Ролля: она непрерывна на отрезке 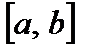 (так как
(так как 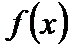 непрерывна), она дифференцируема на
непрерывна), она дифференцируема на 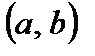 :
:
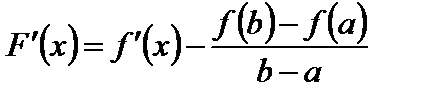 , (5)
, (5)
кроме того, 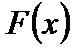 принимает на концах отрезка
принимает на концах отрезка 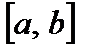 одинаковые значения:
одинаковые значения: 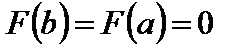 . Следовательно, по теореме Ролля существует такая точка
. Следовательно, по теореме Ролля существует такая точка 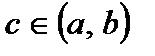 , что
, что 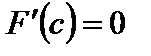 . Но тогда (см. (5))
. Но тогда (см. (5))
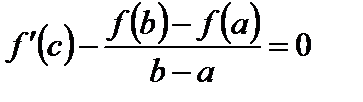 ,
,
т.е. справедливо равенство (3). Теорема доказана.
Заметим, что из (3) непосредственно следует равенство
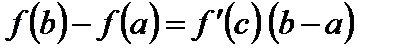 . (6)
. (6)
Эта формула (6) называется формулой Лагранжа.
Рассмотрим пример применения формулы Лагранжа.
Пусть  . Что больше:
. Что больше: 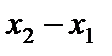 или
или 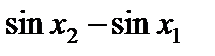 ?
?
Чтобы ответить на этот вопрос, рассмотрим 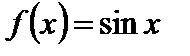 . Имеем
. Имеем 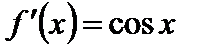 . В соответствии с формулой (6) при
. В соответствии с формулой (6) при 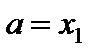 ,
, 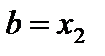 :
:
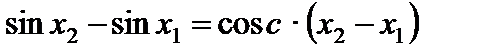 .
.
Но 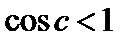 , следовательно,
, следовательно, 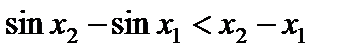 .
.
4. Теорема Коши.Пусть функции 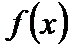 и
и 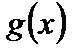 непрерывны на
непрерывны на 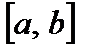 и дифференцируемы на
и дифференцируемы на 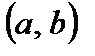 , причем
, причем 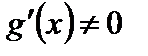 . Тогда существует такая точка
. Тогда существует такая точка 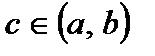 , что справедлива формула
, что справедлива формула
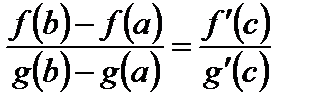 . (7)
. (7)
Доказательство этой теоремы приводить не будем.
Заметим, что теорема Лагранжа есть частный случай теоремы Коши при 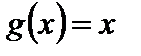 .
.
Правило Лопиталя
Будем говорить, что отношение двух функций 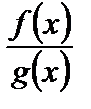 при
при 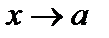 есть неопределенность вида«
есть неопределенность вида« 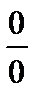 », если
», если
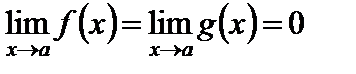 . (8)
. (8)
Можно доказать, что в этом случае (т.е. при условии (8)) верна формула
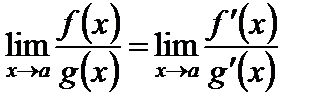 . (9)
. (9)
Формула (9) дает правило вычисления пределов 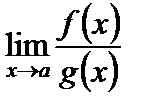 при условии (8). Это правило называется правилом Лопиталя.
при условии (8). Это правило называется правилом Лопиталя.
(Заметим, что вычисление 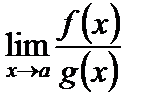 при
при 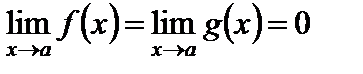 называют раскрытием неопределенности вида «
называют раскрытием неопределенности вида « 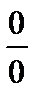 ».)
».)
Рассмотрим на примерах применение правила Лопиталя:
1) 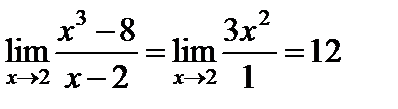 ;
;
2) 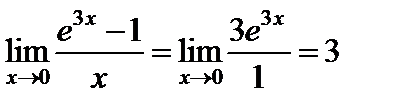 ;
;
3) 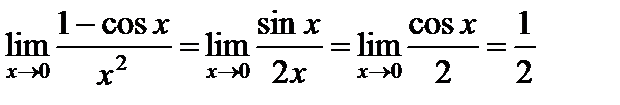 .
.
(Здесь мы дважды последовательно применили правило Лопиталя.)
Будем называть отношение 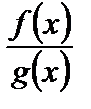 при
при 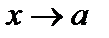 неопределенностью вида «
неопределенностью вида « 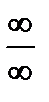 », если
», если
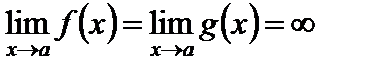 . (10)
. (10)
Для раскрытия неопределенностей « 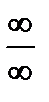 » также применимо правило Лопиталя, т.е. при условии (10) применяется формула
» также применимо правило Лопиталя, т.е. при условии (10) применяется формула
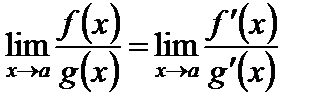 .
.
Это правило применяется также и при 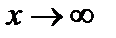 .
.
Примеры:
1) 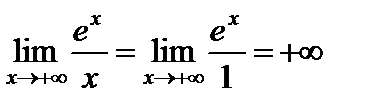 ;
;
2) 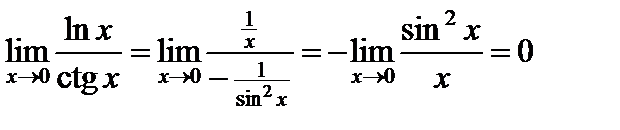 .
.
Заметим, что неопределенности других видов: « 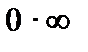 », «
», « 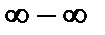 », «
», « 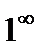 » и т.д.* можно свести к неопределенностям «
» и т.д.* можно свести к неопределенностям « 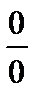 » или «
» или « 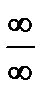 » и затем раскрыть по правилу Лопиталя.
» и затем раскрыть по правилу Лопиталя.
