Исследований функций и построение графиков

Рассмотрим приложения производной к исследованию поведения функций.

Возрастание и убывание функций

Теорема. Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка Х, то функция возрастает (соответственно убывает) на этом промежутке.

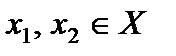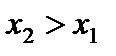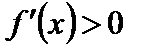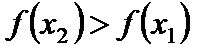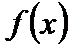Доказательство. Пусть ; ; . Надо доказать, что . Для на отрезке 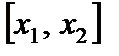выполняются условия теоремы Лагранжа. Поэтому

,

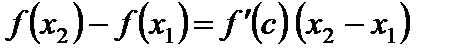где 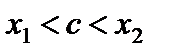. По условию 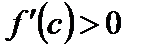, следовательно, 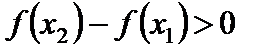. Отсюда 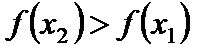. Теорема доказана.

Аналогично доказывается, что если производная отрицательна внутри некоторого промежутка, то функция убывает на этом промежутке.

Доказанная теорема дает достаточное условие возрастания (убывания) функции.

Необходимое условие монотонности формулируется следующим образом:

если функция 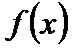возрастает (убывает) на некотором промежутке, то 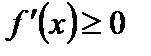(соответственно 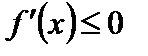) на этом промежутке.

Итак,

1) если 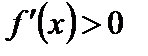, то 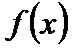возрастает;

2) если 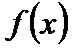возрастает, то 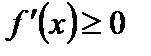, т.е. в отдельных точках производная возрастающей функции может равняться нулю.

Аналогичные утверждения верны для убывающей функции.

Экстремумы

Определение 1. Точка 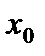называется точкой максимума функции 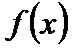, если в некоторой окрестности точки 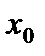выполняется неравенство .

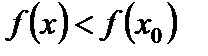Определение 2. Точка 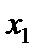называется точкой минимума функции 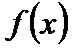, если в некоторой окрестности точки 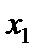выполняется неравенство .

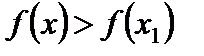Значения функции в точках 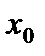и 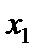называются соответственно максимумоми минимумом функции (т.е. 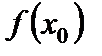– максимум, 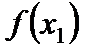– минимум).

Общий термин для максимума и минимума – экстремум.

Необходимое условие экстремума. Если в точке 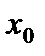дифференцируемая функция 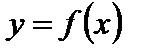имеет экстремум, то в некоторой окрестности этой точки выполнены условия теоремы Ферма, следовательно, 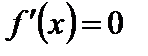. Но функция может иметь экстремум и в точках, в которых она не дифференцируема. Поэтому необходимое условие экстремума можно сформулировать следующим образом.

Для того чтобы функция 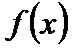имела экстремум в точке 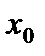, необходимо, чтобы ее производная в этой точке равнялась нулю ( 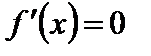) или не существовала.

Точки, в которых выполняется необходимое условие экстремума (т.е. точки, в которых производная равна нулю или не существует), называются критическими (или стационарными).

Итак, если в какой-либо точке имеется экстремум, то эта точка критическая. Заметим, что обратное утверждение неверно. Критическая точка не всегда является точкой экстремума.

Пример. 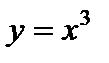. В точке 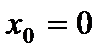производная этой функции равна нулю. Но в этой точке нет ни минимума, ни максимума.

Первое достаточное условие экстремума. Если при переходе через точку 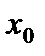производная дифференцируемой функции 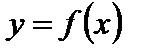меняет знак с плюса на минус, то в точке 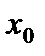имеется максимум, а если с минуса на плюс, то – минимум.

Доказательство. Пусть производная меняет знак с плюса на минус, т.е. в некотором интервале 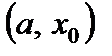выполняется условие 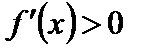, а в некотором интервале 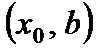– условие 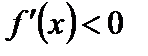. Тогда функция 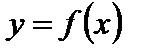возрастает на интервале 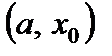и убывает на интервале 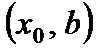. Поэтому 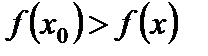и для 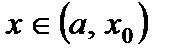, и для 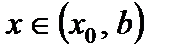, т.е. 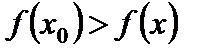для всех 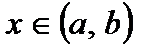. А это значит, что в точке 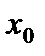– максимум.

Для случая, когда производная меняет знак с минуса на плюс, доказательство аналогично.

Заметим, что если изменения знака не происходит, то экстремума нет.