Линейные ур-ния.Метод вариации.

Определение 6. Уравнение вида

У' + Р (х) *У = f(х),

где P (х) и f (х) — непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Название уравнения объясняется тем, что неизвестная функция у и ее производная у' входят в уравнение линейно, т. е. в первой степени.

Если f(х) == 0(тождественно), то уравнение (10) называется линейным однородным уравнением

Для нахождения общего решения уравнения (10) может применен метод вариации постоянной.

В этом методе сначала находят общее решение линейного однородного уравнения

у' + р(х)у = О, (11)

соответствующего данному неоднородному уравнению (10). Ур-нение (11) является уравнением с разделяющимися переменными; Разделяя переменные и интегрируя, имеем

dy/y= -р(х) dх,

lnlyl = - S р (х)dx+ln IC1 I

lyl/lc1l=-Sp(x)dx

Отсюда, потенцируя, находим общее решение уравнения (11):

у = ±С1*e ^-Sр(х)dх, или у = С*e^ -Sр(х)dх, где у = ±С1*e^ -Sр(х)dх, или у = С*e ^-Sр(х)dх, где

С = ±C1 — произвольная постоянная.

Теперь найдем общее решение Ур(10) в виде (12), где С будем принимать не постоянной, а новой неизв функцией от х, т.е. в виде

y=C(x)*e^-Sp(x)dx

Чтобы найти функцию С (х) и, тем самым, решение в виде (13), ставим функцию (13) в уравнение (10). Получим

C'(x)*e^-Sp(x)dx-C(x)*p(x)*e^(-Sp(x)dx)+p(x)*C(x)*e^-Sр(х)dх=f(x)

или c'(x)=f(x)*e^Sр(х)dх(14)

Итак чтобы функция (13) являлась решением уравнения(10), функця С (х) должна удовлетворять уравнению (14). Интегрируя находим

C(x)=Sf(x)*e^(Sр(х)dх)dx+c1

С1 — произвольная постоянная. Подставляя найденное выра-ие для С (х} в соотношение (13), получаем общее решение линейного уравнения (10):

. y(x)=c1*e^-Sр(х)dх+e^-sр(х)dх*Sf(x)*e^S(р(х)dх)dx(15)

1. Понятие первообразной. Основные свойства (лемма, теорема)

2. Понятие неопределенного интеграла.

3. Методы замены переменной

4. Метод интегрирования по частям.

5. Основные типы интегралов берущихся по частям.

6. Теорема о представлении рациональной функции в виде суммы элементарных дробей с неопределенными коэффициентами.

7. Метод неопределенных коэффициентов.

8. Основные типы интегралов от рациональных функций.

9. Понятие интегральной суммы. Геометрический смысл.

10. Понятие определенного интеграла.

11. Основные свойства определенного интеграла.

12. Интеграл с переменным верхним пределом.

13. Формула Ньютона-Лейбница.

14. Замена переменных в определенном интеграле.

15. Формула интегрирования по частям в определенном интеграле.

16. Приближенное вычисление определенного интеграла.

17. Несобственные интегралы с бесконечными пределами.

18. Несобственные интегралы от неограниченных функций.

19. Метрические, линейные, нормированные, евклидовы пространства.

20. Понятие функции N переменный. Предел функции N переменных.

21. Непрерывность функции N переменных.

22. Непрерывность сложной функции.

23. Частные производные функции N переменных.

24. Дифференцируемость функции N переменных.

25. Дифференциал функции N переменных.

26. Дифференцирование сложной функции.

27. Производная по направлению. Градиент.

Частные производные высших порядков функции N переменных.
Таблица основных интегралов:

2. ò0dx=C

3. òdx=x+C

4. òх^a dx=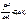

5. òа^хdx=а^х/lna+C

6. òdx/x=ln|x|+C

7. òe^хdx=e^х+C

8. òsinxdx=-cosx+C

9. òcosxdx=sinx+C

10. òdx/cos²x=tgx+C

11. òdx/sin²x=-ctgx+C

12. òdx/ 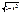=arcsinx +C=-arccosx+c

13. òdx/1+x²=arctgx+C=-arcctgx+C

14. òdx/x²+ a² =1/a arctgx/a+C

15. òdx/x²-a² =1/2a ln|x-a/x+a|+C

16. òdx/ 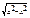=arcsin x/a +C

17. òdx/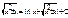

28.

29. Дифференциал второго порядка функции N переменных.

30. Квадратичная форма. Критерий Сильвестра.

31. Локальный экстремум функции N переменных. Необходимое условие локального экстремума.

32. Достаточные условия локального экстремума функции N переменных.

33. Неявные функции.

34. Условный экстремум

35. Метод множителей Лагранжа.

36. Определение числового ряда, частичной суммы, сходящегося ряда.

37. Свойства сходящихся числовых рядов.

38. Необходимое условие сходимости числового ряда. Сходимость гармонического ряда.

39. Необходимое и достаточное условие сходимости ряда с неотрицательными членами.

40. Признак сравнения.

41. Признак Даламбера.

42. Интегральный признак Коши.

43. Знакочередующийся ряд. Признак Лейбница.

44. Знакопеременные ряды, их сходимость.

45. Степенные ряды.

46. Теорема Абеля.

47. Теорема об интервале сходимости степенного ряда.

48. Теорема о радиусе сходимости степенного ряда

49. Понятие двойного интеграла.Геометрический смысл двойного интеграла

50. Свойства двойного интеграла

51. Переход от двойного интеграла к повторному для прямоугольной области

52. Переход от двойного интеграла к повторному для криволинейной области Приложение двойного интеграла

53. Дифференциальные уравнения первого порядка. Задача Коши. Общие и частные решения дифференциального уравнения

54. Уравнения с разделяющимися переменными.

55. Линейные уравнения . Метод вариации.

Таблица основных интегралов:

18. ò0dx=C

19. òdx=x+C

20. òх^a dx=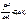

21. òа^хdx=а^х/lna+C

22. òdx/x=ln|x|+C

23. òe^хdx=e^х+C

24. òsinxdx=-cosx+C

25. òcosxdx=sinx+C

26. òdx/cos²x=tgx+C

27. òdx/sin²x=-ctgx+C

28. òdx/ 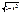=arcsinx +C=-arccosx+c

29. òdx/1+x²=arctgx+C=-arcctgx+C

30. òdx/x²+ a² =1/a arctgx/a+C

31. òdx/x²-a² =1/2a ln|x-a/x+a|+C

32. òdx/ 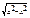=arcsin x/a +C

33. òdx/