Линейных систем с постоянными коэффициентами

Задачи оптимизации, в которых производится минимизация времени перехода из начального состояния в конечное, называются задачами об оптимальном (максимальном) быстродействии. Рассмотрим случай линейной системы с постоянными коэффициентами:

.

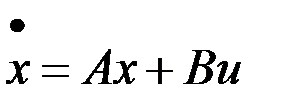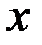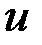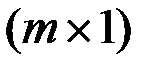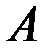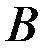Здесь - вектор состояния , - вектор управления , и - постоянные матрицы порядков 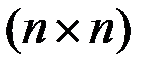и 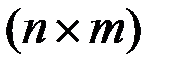. Будем полагать, что компоненты вектора управления ограничены по величине:

, .

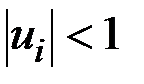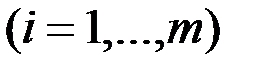В задачах об оптимальном быстродействии критерий оптимальности имеет вид

.

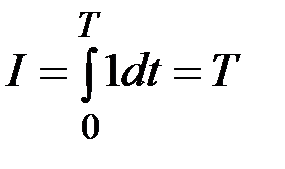Для выявления структуры оптимального управления воспользуемся необходимыми условиями в задаче Лагранжа. Составим гамильтониан

,

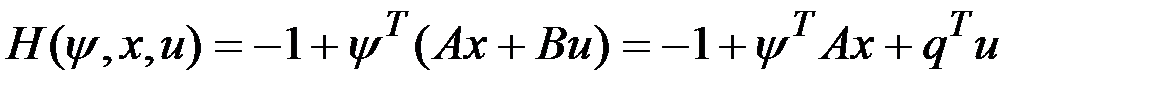где , .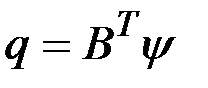

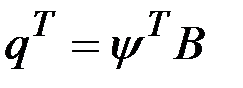Каноническая система уравнений принимает вид

, ,

, .

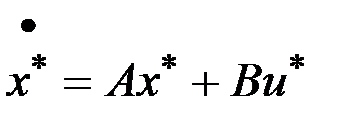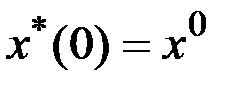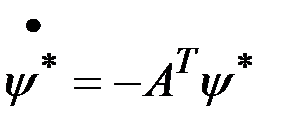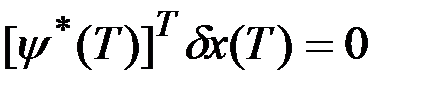Оптимальное управление 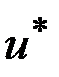определяется из условия максимизации гамильтониана:

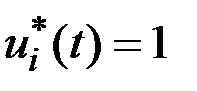, если 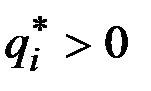, , 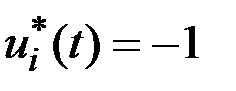если 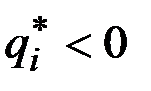, , 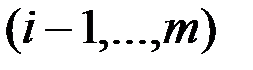или в векторной форме .

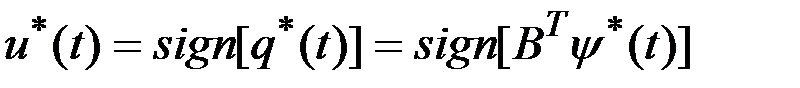Если 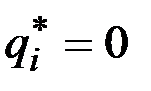на некотором отрезке времени , то задача называется вырожденной, а управление может быть любым, поскольку гамильтониан от него не зависит. Однако в данной постановке случай вырожденности не имеет места.

Так как 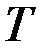свободно, 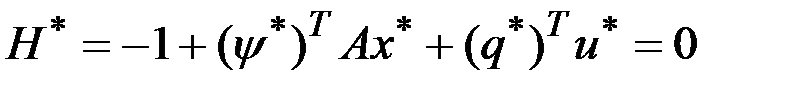или 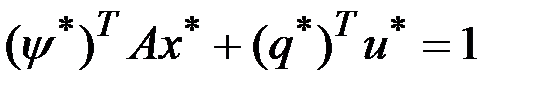для любого 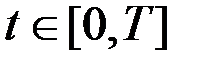. Отсюда следует, что 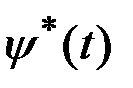- ненулевой вектор для всех 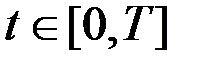, задача не вырождена.

Если задача вырождена, а все корни характеристической системы, соответствующей рассматриваемой математической модели, являются действительными числами, то можно доказать, что оптимальное управление имеет не более 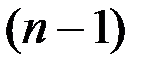переключений. В случае комплексных корней число переключений также конечно, но зависит от начального и конечного состояния системы.

Предположим, что алгоритм решения канонической системы существует. Тогда для каждого момента времени 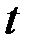могут быть найдены векторы 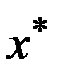, 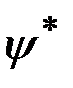и установлена (в общем случае численно) зависимость 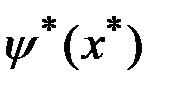. Фактически получается решение задачи синтеза оптимального управления:

,

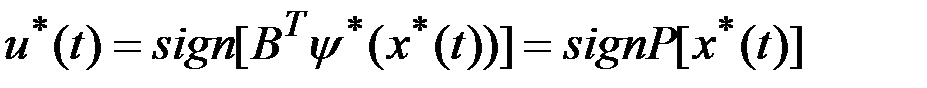где функция 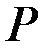называется функцией переключения.

Оптимальное управление линейной системой

С квадратичным функционалом

1. Задача программирования оптимального управления

Рассмотрим линейную динамическую систему

, , , ,

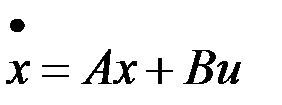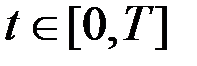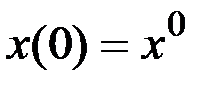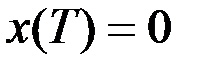где 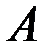и 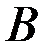- матрицы порядков 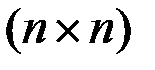и 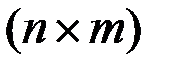, зависящие от времени, 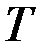- фиксировано, 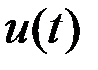- не ограничено.

Критерий оптимальности зададим в виде

,

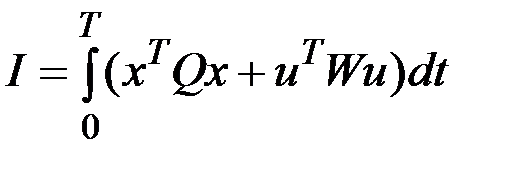где 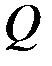и 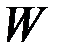- положительно определенные матрицы порядков 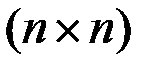и 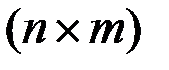, зависящие от времени.

Для определения оптимального управления 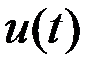, минимизирующего функционал 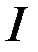, используем принцип максимума, Составим гамильтониан 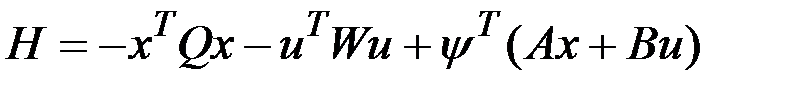. Оптимальное управление определим из условий максимума :

, .

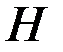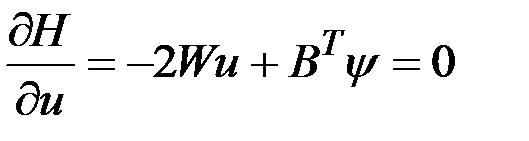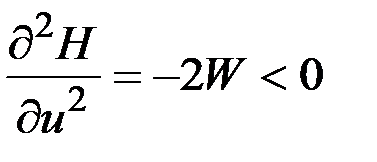Второе условие выполняется, поскольку - положительно определенная матрица. Следовательно, в соответствии с первым условием оптимальный закон управления имеет вид программы

.

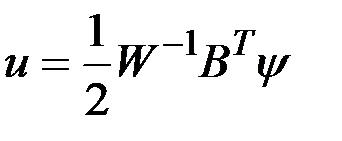Каноническая система уравнений принимает вид

, , ,

.

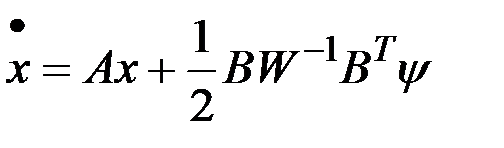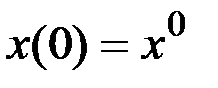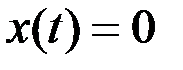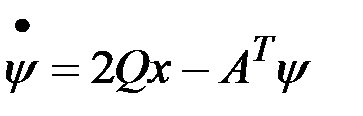Получили краевую задачу для системы линейных дифференциальных уравнений.

2. Задача синтеза оптимального управления

Рассмотрим задачу синтеза оптимального управления системой

, ,

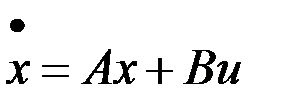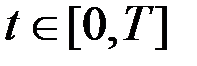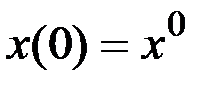
из условия обращения в минимум критерия оптимальности

.

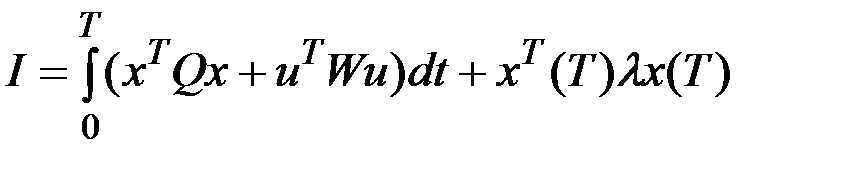Полагаем, что 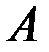, , 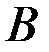, 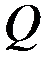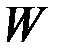- матрицы, зависящие от времени, причем 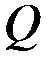, , 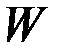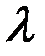- положительно определенные, 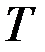- фиксировано.

Как и в предыдущей задаче в соответствии с принципом максимума оптимальное управление определяется зависимостью

.

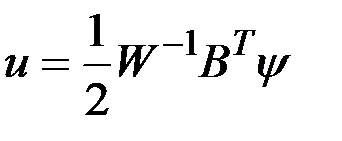Каноническая система уравнений имеет также прежнюю структуру, но другие граничные условия:

, , ,

, .

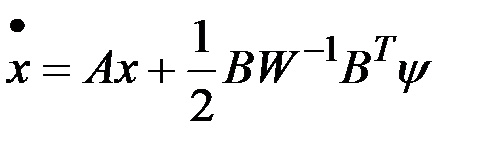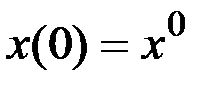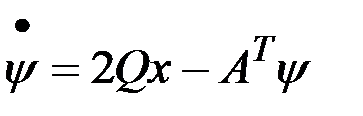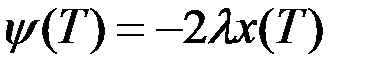Если решение второго уравнения искать в виде 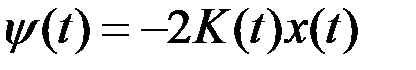, то для матрицы 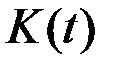можно получить уравнение, которое позволит найти ее непосредственно:

, .

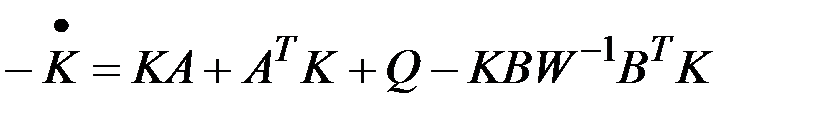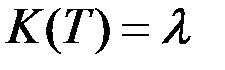Это уравнение представляет собой нелинейное матричное дифференциальное уравнение Риккати. Определив 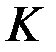, получим закон оптимального управления:

.

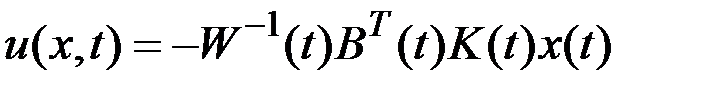Если 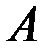, , 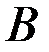, 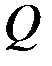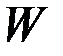не зависят от времени, то при достаточно большом 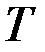можно говорить об «установившемся» режиме. В этом случае полагается 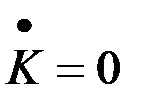. Тогда матрица 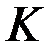является постоянной и определяется из линейного матричного алгебраического уравнения:

.

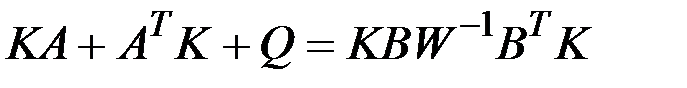Решение этого уравнения можно рассматривать как предел решения дифференциального уравнения Риккати при 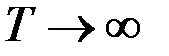, если он существует.