С ограничениями на вектор состояния

Доказательство принципа максимума было проведено без учета ограничений на фазовый вектор. Рассмотрим систему уравнений

, , ,

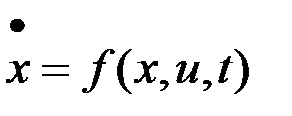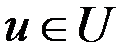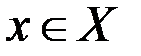
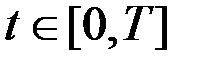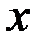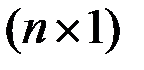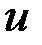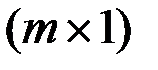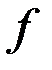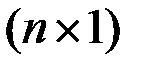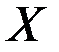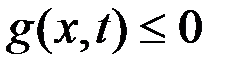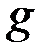где - вектор , - вектор , - вектор , а множество задано в виде , где - вектор-функция 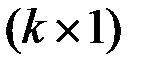, причем .

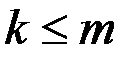Рассмотрим задачу Лагранжа при свободном :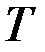

.

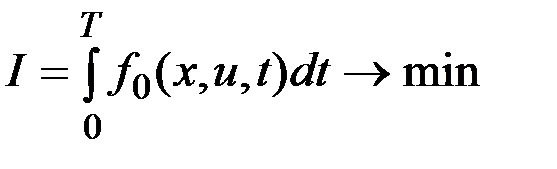Исследуем оптимальные траектории, которые можно разбить на конечное число участков, каждый из которых лежит либо на границе множества 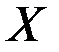, либо внутри него. Пусть оптимальная траектория полностью лежит на границе 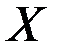, а управляемая система автономна. Чтобы 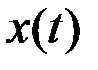принадлежал границе, необходимо и достаточно, чтобы

,

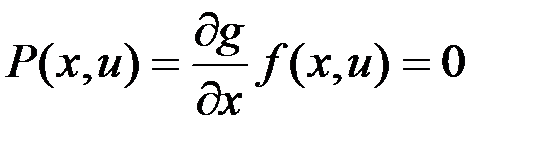т.е. вектор скорости должен быть перпендикулярен нормали к поверхности 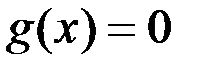. 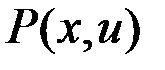- вектор размерности .

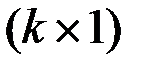Введем в рассмотрение расширенный вектор 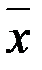, аналогично доказательству принципа максимума. Тогда задача Лагранжа принимает частный виз задачи Майера:

, , , ,

.

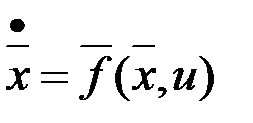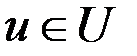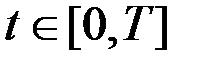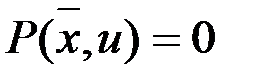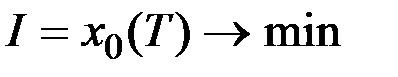Получим необходимые условия оптимальности. Дадим оптимальному управлению 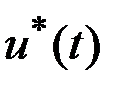игольчатую вариацию при 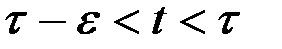. Вариация траектории при 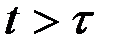определяется из уравнения в приращениях

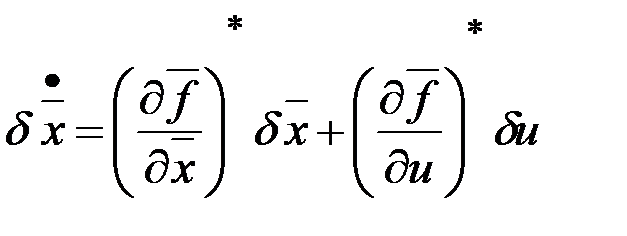
с начальным условием .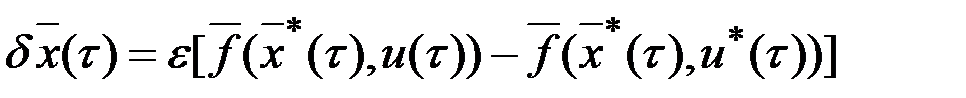

Связь вариаци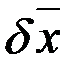й и 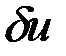определим, продифференцировав уравнение :

.

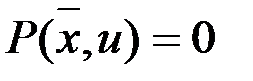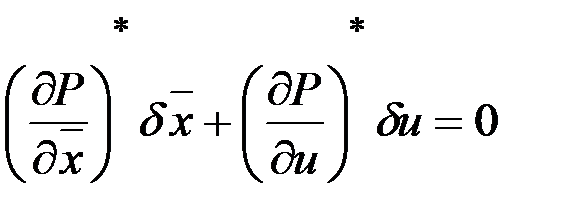Исключим 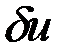из уравнения для вариации траектории. Умножим последнее уравнение на некоторую матрицу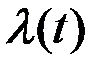 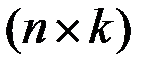и прибавим к уравнению для вариации траектории:

.

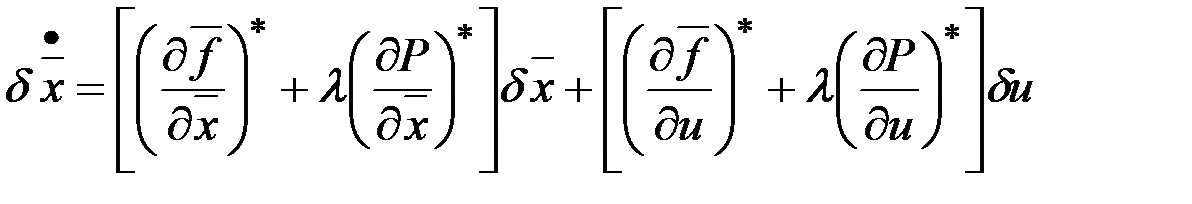Потребуем, чтобы матрица 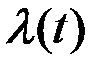обеспечивала равенство

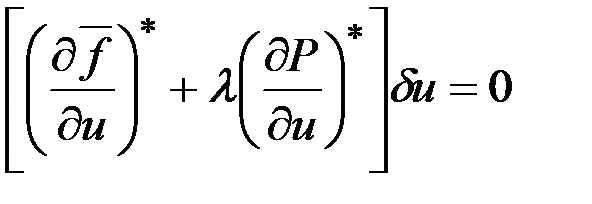для всех .

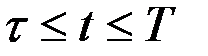Тогда .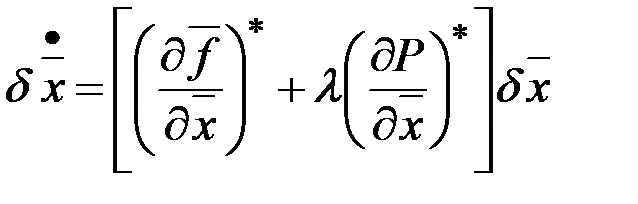

Введем вектор 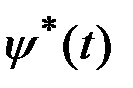, такой, чтобы

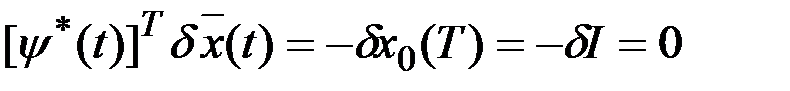для всех .

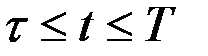Отсюда следует, что при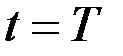

, .

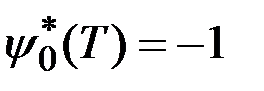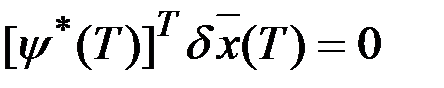Дифференцируя предпоследнее равенство по времени и учитывая выражение для производной 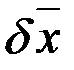, получим следующее уравнение для сопряженных множителей

.

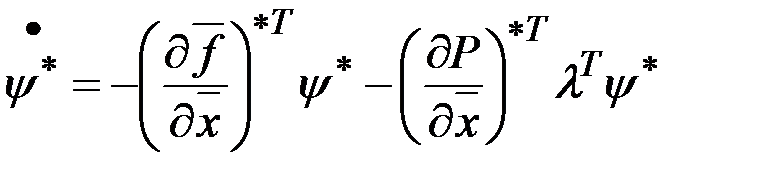Определив вектор 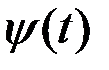согласно последним выражениям и введя функцию Гамильтона 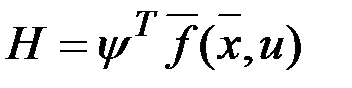, получим для момента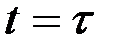

.

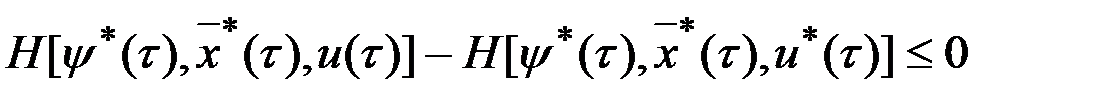Или .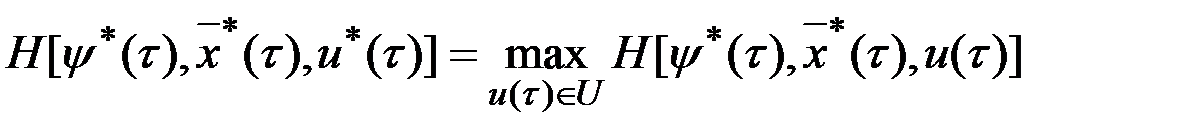

Так как 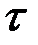может быть любым из 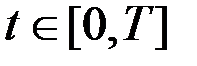, то окончательно

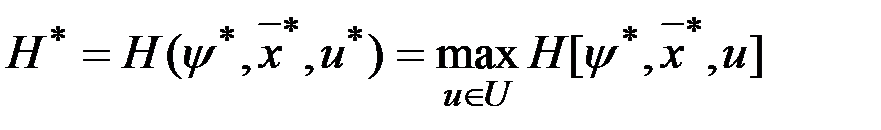для всех .

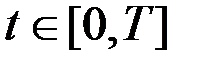Каноническая система уравнений имеет вид

, ,

,

, .

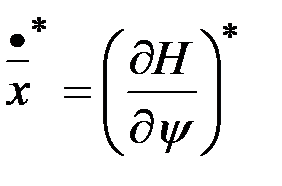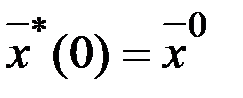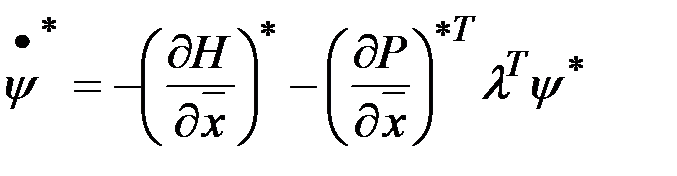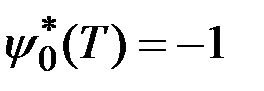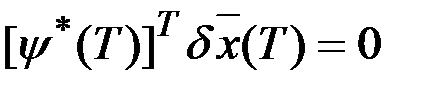Кроме того, должно выполняться условие .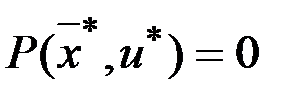

Определим матрицу 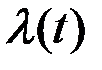. По определению

.

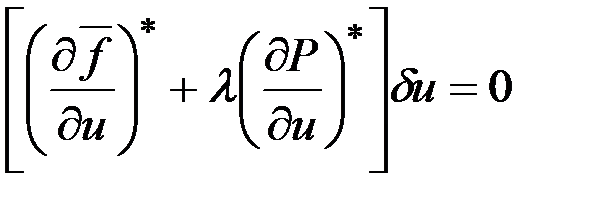Пусть 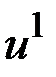и 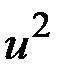- составляющие вектора 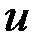, такие, что 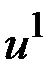имеет размеры 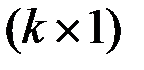, а 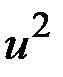- 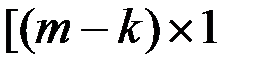, а матрица 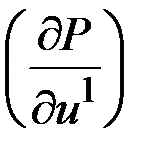- неособенная с размером 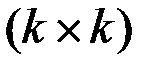. Вариаци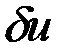и и 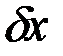связаны 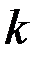соотношениями

.

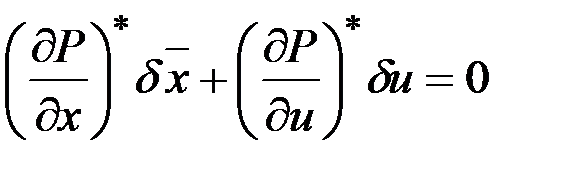Поэтому 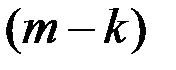компонентов 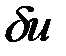, например, 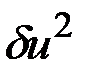, можно считать свободными. Зададим 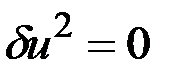, тогда

.

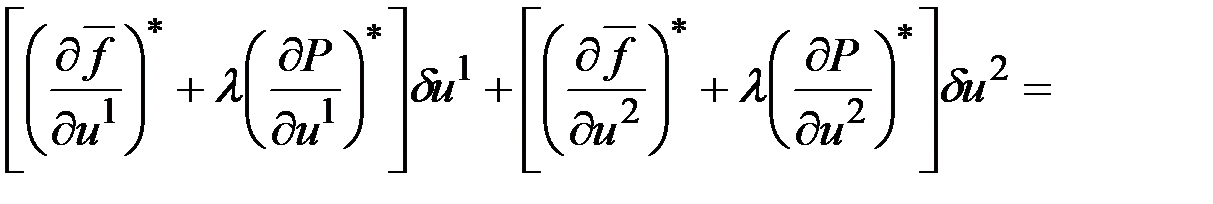
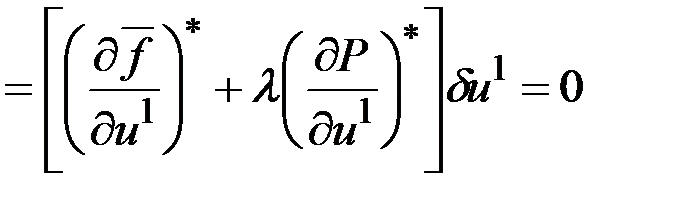Следовательно, достаточно задать 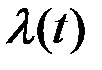следующим образом

.

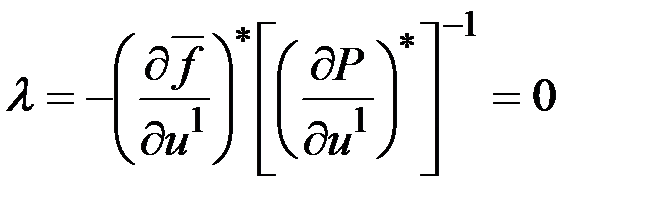Таким образом, для рассматриваемой задачи необходимые условия оптимальност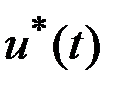и и 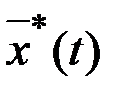имеют вид:

1. , ,

,

, ,

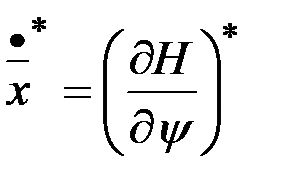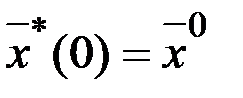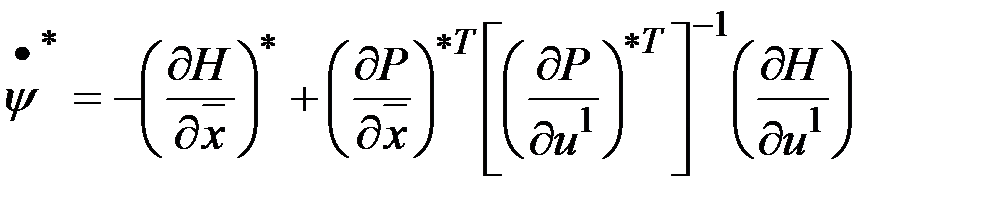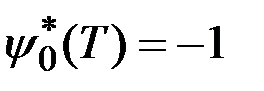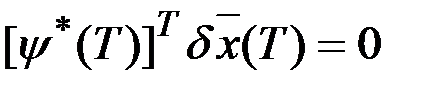где 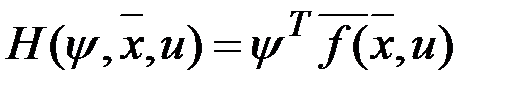, 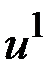- вектор, составленный из любых 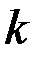компонентов вектора 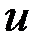, таких, что матрица 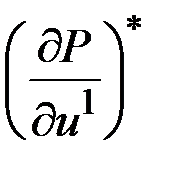неособенная, 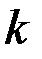- размерность вектора ;

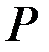2. 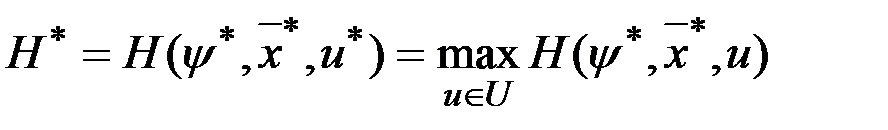для всех 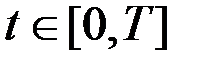при условии ;

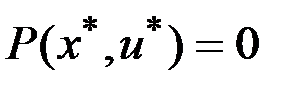3. 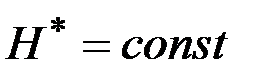, если 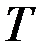фиксировано,

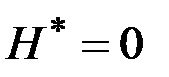, если свободно для всех .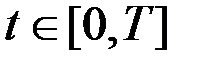

Для исходной задачи Лагранжа необходимые условия оптимальности записываются также, но для нерасширенного вектора состояния 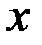при отсутствии условия 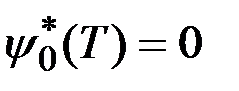и гамильтониана, имеющего вид: .

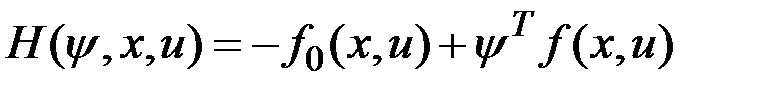Можно получить обобщения на другие случаи, в частности, для неавтономной системы.

Получим условия стыковки участков оптимальной траектории. Предположим, что оптимальная траектория состоит из конечного числа участков, каждый из которых лежит либо внутри области 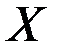, либо на ее границе 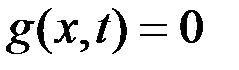. Имеет место следующее свойство оптимальной траектории. В классе кусочно-непрерывных управлений каждый участок оптимальной траектории является оптимальным в смысле общего критерия, рассматриваемого лишь на данном участке. Обозначив через 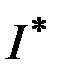минимальное значение функционала, а через 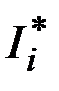минимальное значение функционала на 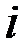-ом участке, можно утверждать, что .

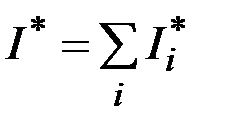В соответствии с этим свойством, на любом участке оптимальной траектории выполняются необходимые условия оптимальности. Определим условия, которым должна удовлетворять оптимальная траектория в точках стыка участков, т.е. при переходе от одного участка к другому. Рассмотрим переход от участка, лежащего внутри допустимой области на участок, лежащий на ее границе, т.е. отрезок времени 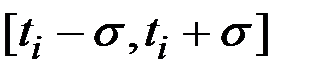, где - сколь угодно малая величина, а 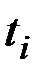- момент входа оптимальной траектории на участок границы 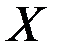, описываемый уравнением 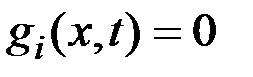, где 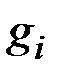- вектор-функция размерности .

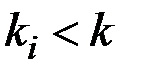Функционал на участке 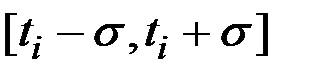записывается следующим образом

.

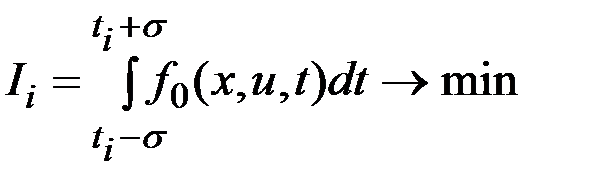Для рассматриваемого бесконечно малого участка оптимальной траектории 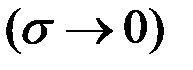составляется гамильтониан и выводятся соотношения, связывающие величины до момента 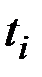и после него:

,

,

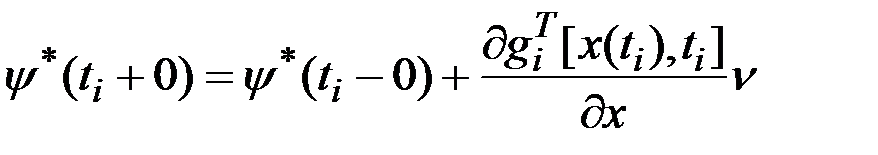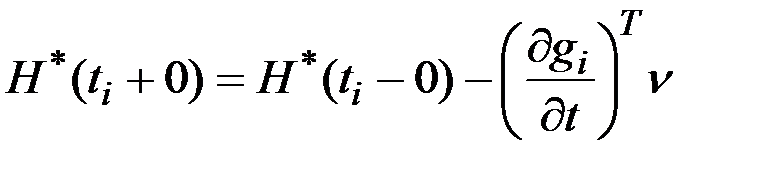где 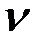- вектор размерности 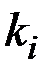. Эти соотношения называются условиями скачка.

Таким образом, если оптимальная траектория существует и содержит конечное число точек стыка, то каждый участок, лежащий внутри допустимой области 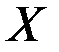, удовлетворяет принципу максимума без ограничений на фазовый вектор, каждый участок, лежащий на границе, удовлетворяет принципу максимума с ограничениями на фазовый вектор, а в каждой точке стыка выполняются условия скачка гамильтониана и сопряженных переменных.

Связь принципа максимума