Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.

Рассмотрим еще один метод интегрирования нормальной системы уравнений (6.1) в случае, когда она представляет собой систему линейных однородных ДУ с постоянными коэффициентами, т. е. систему вида 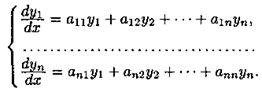. Для простоты ограничимся рассмотрением системы трех уравнений с тремя неизвестными функциями y1, у2 и у3: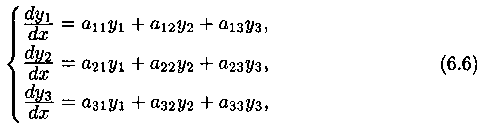

где все коэффициенты аij (i,j= 1,2,3) - постоянные. Будем искать частное решение системы (6.6) в виде: 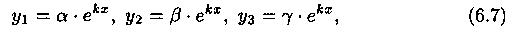где а, β, γ, k - постоянные, которые надо подобрать (найти) так, чтобы функции (6.7) удовлетворяли системе (6.6). Подставив эти функции в систему (6.6) и сократив на множитель 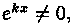получим: 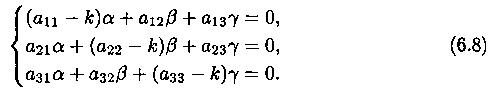Систему (6.8) можно рассматривать как однородную систему трех алгебраических уравнений с тремя неизвестными а, β, γ. Чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель системы был равен нулю: 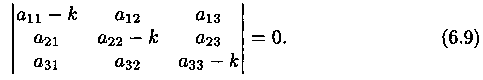Уравнение (6.9) называется характеристическим уравнением системы (6.6). Раскрыв определитель, получим уравнение третьей степени относительно К. Рассмотрим возможные случаи. Случай 1. Корни характеристического уравнения действительны и различны: k1 k2, k3. Для каждого корня ki (i=1,2,3) напишем систему (6.8) и определим коэффициенты 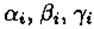(один из коэффициентов можно считать равным единице). Таким образом, получаем: для корня k1 частное решение системы (6.6): 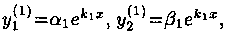для корня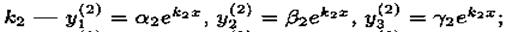

для корня 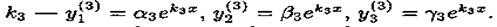Можно показать, что эти функции образуют фундаментальную систему, общее решение системы (6.6) записывается в виде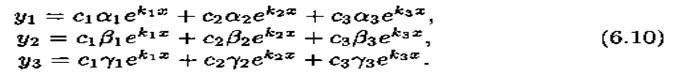

Случай 2. Корни характеристического уравнения различные, но среди них есть комплексные: 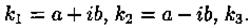Вид частных решений в этой ситуации определяют так же, как и в случае 1.

Замечание. Вместо полученных частных решений можно взять их линейные комбинации, применяя формулы Эйлера; в результате получим два действительных решения, содержащих функции вида 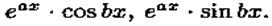Или, выделяя действительные и мнимые части в найденных комплексных частных решениях, получим два действительных частных решения (можно показать, что они тоже являются решениями уравнения). При этом понятно, что комплексно-сопряженный корень k2=а- ib не даст новых линейно независимых действительных решений.

Случай 3. Характеристическое уравнение имеет корень k кратности m (m=2,3). Решение системы, соответствующее кратному корню, следует искать в виде: а) если m=2, то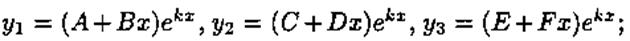

б)если m=3, то ,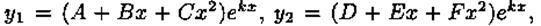

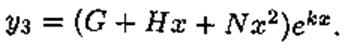Это решение зависит от m произвольных постоянных. Постоянные А,В,С,... ,N определяются методом неопределенных коэффициентов. Выразив все коэффициенты через m из них, полагаем поочередно один из них равным единице, а остальные равными нулю. Получим m линейно независимых частных решений системы (6.6)

23.Устойчивость решений дифференциальных уравнений.Асимптотическая устойчивость. Поскольку при решении реальных задач с помощью дифференциальных уравнений начальные условия обычно являются результатами измерений и, следовательно, получены с некоторой погрешностью, очень важным является вопрос о том, как изменится решение уравнения при малом изменении начальных условий. В частности, если такие изменения существенно меняют решение, то подобное решение, очевидно, не имеет практической ценности.

Пусть некоторое явление описывается системой дифференциальных уравнений 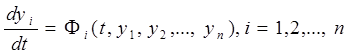(24.1) с начальными условиями y_i(t₀) = y_i0 .

Определение 24.1. Решение φ_i (t) (ǐ = 1,2,…,n) называется устойчивым по Ляпунову, если 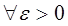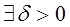такое, что для всякого решения y_i (t) той же системы, начальные условия которого удовлетворяют неравенствам 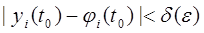, для всех 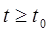справедливы неравенства 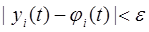(24.2) (то есть близкие по значениям решения остаются близкими для всех 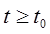).Если хотя бы для одного решения y_i (t) неравенства (24.2) не выполняются, решение φ_i (t) называется неустойчивым. Если решение φ_i (t) не только устойчиво по Ляпунову, но и удовлетворяет условию 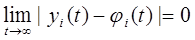(24.3)

при 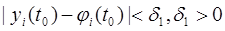, то это решение называется асимптотически устойчивым. Замечание. Одно условие (24.3) не обеспечивает устойчивость решения.

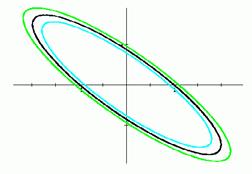
На рисунке чёрным изображена устойчивая фазовая траектория, некой системы дифференциальных уравнений второго порядка, которая начинается в точке (1, 0), и две, начинающиеся вблиз неё траектории.

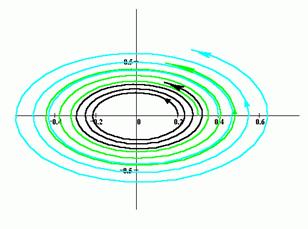
На рисунке чёрным изображена неустойчивая фазовая траектория, некой системы дифференциальных уравнений второго порядка, которая начинается в точке (0.2, 0), и две, начинающиеся вблиз неё траектории

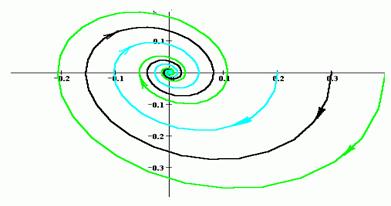На рисунке чёрным изображена асимптотически устойчивая фазовая траектория, некой системы дифференциальных уравнений второго порядка, которая начинается в точке (0.3, 0), и две, начинающиеся вблизи неё, траектории.