Формула полной вероятности. Формулы Байеса (теорема гипотез)

Пусть случайный эксперимент можно описать событиями H₁,H₂,…,H_т, которые являются попарно несовместными 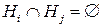, 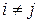и их объединение достоверное событие 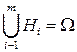. Такие события Н_i называют гипотезами. Предполагается, что событие А может произойти с одной из гипотез Н_i.

Вероятность любого события А, которое может произойти с одной из гипотез Н_i, будет равна сумме произведений вероятностей гипотез на условную вероятность события А,т.е. вычисляется по формуле:

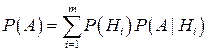, (3.1)

которая называется формулой полной вероятности.

Безусловные вероятности 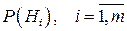, рассматриваются как априорные (доопытные) вероятности гипотез.

Предположим, что эксперимент произведен и в результате произошло событие А. Как изменится при этом апостериорная (послеопытная) вероятность гипотез H_k?

Условные вероятности гипотез Н₁,Н₂,…,Н_т при условии, что событие А имело место, вычисляются по формулам Байеса:

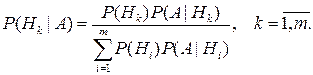(3.2)

Задачи

3.1.В некоторую торговую точку поступает определенного вида товар от двух производителей. Известно , что первый производитель поставляет 40% этого товара, а второй - 60%. Опыт показывает, что, как правило, 2% изделий первого производителя содержат брак, а для второго производителя брак составляет 3%. Определить вероятность того, что случайно отобранное изделие содержит брак.

Решение. Из условия задачи следует, что рассматриваемое событие А={случайно отобранное изделие содержит брак} может произойти с одной из гипотез Н_i: i =1,2. Н_i={изделие поставлено i-ым производителем}.

Безусловные априорные вероятности этих гипотез легко вычисляются по классической формуле (1.1):

; .

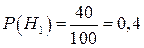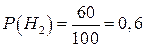Условные вероятности событий А|H_i ={бракованное изделие поставлено i-ым производителем}, i=1,2, так же определяется по формуле(1.1):

; .

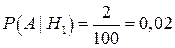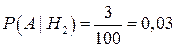Применив формулу полной вероятности (3.1), получим искомую вероятность:

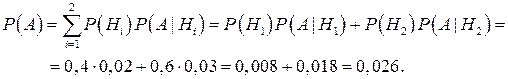
Находясь в условиях этой же задачи, предположим, что выбранное изделие содержит брак. Тогда определим вероятность того, что это изделие поставил первый поставщик, воспользовавшись формулой Байеса:

‌

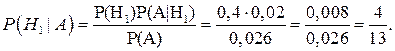
Ответ: Р(А)=0,026; .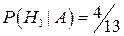

3.2.Партия транзисторов, среди которых 10% дефектных, поступила на проверку. Схема проверки такова, что с вероятностью 0,95 обнаруживают дефект (если он есть), и существует ненулевая вероятность 0,03 того, что исправный транзистор будет признан дефектным. Какова вероятность того, что случайно выбранный из партии транзистор будет признан дефектным?

3.3.В продажу поступают телевизоры трех заводов. Продукция первого завода содержит 20% телевизоров со скрытым дефектом, второго – 10%, третьего – 5%. Какова вероятность приобрести неисправный телевизор, если в магазин поступило 30% телевизоров с первого завода, 20% – со второго, 50% – с третьего?

3.4.В ящике лежит 20 теннисных мячей, в том числе 15 новых и 5 использованных в игре. Для игры наудачу выбирается 2 мяча и после игры возвращаются обратно. Затем для второй игры также наудачу извлекаются еще 2 мяча. Какова вероятность того, что вторая игра будет проводиться новыми мячами?

3.5.Из десяти студентов, пришедших сдавать экзамен по теории вероятностей и взявших билеты, Иванов и Петров знают 20 билетов из 30, Сидоров успел повторить только 15 билетов, остальные студенты знают все 30 билетов. По прошествии отведенного времени на подготовку экзаменатор наудачу вызывает отвечать одного из студентов. Какова вероятность того, что студент сдаст экзамен, если знание билета гарантирует сдачу экзамена с вероятностью 0,85, а при незнании билета, можно сдать экзамен лишь с вероятностью 0,1?

3.6.Для контроля продукции из трех партий деталей взята для испытаний одна деталь. Как велика вероятность обнаружения бракованной продукции, если в одной партии 2/3 деталей бракованные, а в других – все доброкачественные?

3.7.Число бракованных микросхем на 1000 априори (до опыта) считается равновозможным от 0 до 3. Наудачу протестированы 100 микросхем, оказавшиеся исправными. Какова вероятность того, что все схемы исправны?

3.8.Определить вероятность того, что 100 лампочек, взятых наудачу из 1000, окажутся исправными, если известно, что число испорченных лампочек на 1000 штук равновозможно от 0 до 5.

3.9.Известно, что 96% выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодность стандартной продукции с вероятностью 0,98 и нестандартной – с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.

3.10.На фирме работает два бухгалтера – опытный и начинающий. Опытный бухгалтер оформляет 75% документов, а начинающий – 25%. У опытного бухгалтера наличие ошибок в документах составляет 0,5%, у начинающего – 8%. Какова вероятность того, что взятый наудачу документ окажется с ошибкой?

3.11.Рабочий обслуживает 3 станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,03, для второго – 0,05, для третьего – 0,06. Обработанные детали складываются в один ящик. Производительность второго станка в два раза больше, чем первого, а третьего в два раза меньше, чем первого. Какова вероятность того, что взятая наудачу деталь из ящика будет бракованной?

Решение. Введем события: А={взятая наудачу деталь бракованная}, Н_i={деталь изготовлена на i-ом станке}, i=1,2,3. Пусть х – производительность первого станка, тогда 2х – производительность второго и 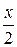– производительность третьего. Общая производительность трех станков равна .

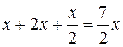Вероятности гипотез Н_i равны:

; ; .

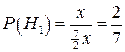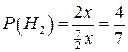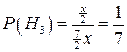Вероятность события А находим по формуле (3.1):

.

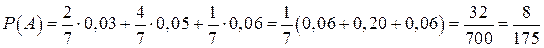Ответ: .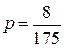

3.12.Фирма совершает сделки, 80% из которых прибыльные, а 20% – неприбыльные. Вероятность банкротства фирмы за время t в случае, когда она заключает прибыльные сделки, равна 0,01, а в случае заключения не прибыльных сделок равна 0,7. Определить вероятность банкротства фирмы за время t.

3.13.При наступлении кризиса сбыта продукции фирма не терпит убытков с вероятностью р₁, полностью терпит банкротство с вероятностью р₂ и имеет серьезные издержки с вероятностью 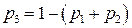. Две серии серьезных издержек приводят к полному банкротству фирмы. Найти вероятность того, что при наступлении п кризисов сбыта продукции фирма не обанкротится.

3.14.В группу, состоящую из 20 студентов, добавили отличника, после чего из нее наудачу перевели в другую группу студента. Определить вероятность того, что переведенный студент окажется отличником, если все предположения о первоначальном составе группы равновозможны.

3.15.Для поиска самолета, потерпевшего аварию, выделено 5 вертолетов, каждый из которых может быть использован для поисков в одном из двух возможных районов, где самолет может находиться с вероятностями 0,7 и 0,3. Как следует распределить вертолеты по районам поисков, чтобы вероятность обнаружения самолета была наибольшей, если каждый вертолет обнаруживает находящийся в районе поисков самолет с вероятностью 0,3, а поиски осуществляются каждым вертолетом независимо от других? Найти вероятность обнаружения самолета при оптимальной процедуре поисков.

3.16.Два предпринимателя занимаются реализацией одинаковой продукции, которая поставляется ими в один и тот же магазин. Первый предприниматель поставляет продукции в 2 раза больше, чем второй, причем продукция высшего качества у него составляет 60 %, а у второго – 84%. Случайный покупатель приобретает продукцию высшего качества. Определить вероятность того, что она поставлена первым предпринимателем.

Решение: Рассматриваемое событие А ={приобретена продукция высшего качества} может произойти из одной из гипотез Н_i, Н_i={продукция поставлена i-ым предпринимателем}, i=1,2. Безусловные доопытные вероятности гипотез вычисляются по классической формуле (1.1):

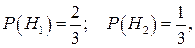
так, как первый предприниматель поставляет в 2 раза больше продукции.

Условные вероятности событий А|Н_i={i-ым предпринимателем поставлена продукция высшего качества}, так же находятся по формуле (1.1):

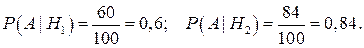
Далее находим вероятность того, что случайный покупатель приобрел продукцию высшего качества, т.е. вероятность события А. Поскольку событие А может произойти с одной из гипотез Н₁ или Н₂, то для нахождения вероятности события А воспользуемся формулой полной вероятности:

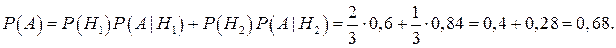
Событие А произошло, т.е. покупатель приобрел продукцию высшего качества, тогда вероятность события А|Н₁={продукция высшего качества поставлена первым предпринимателем} вычислим по формуле Байеса:

‌

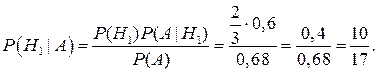
3.17.Возбуждено дело о банкротстве фирмы. Основанием для этого могли быть следующие положения:

1. Заявление предприятия о своем банкротстве.

2. Решение суда о возбуждении дела о банкротстве.

3. Заявление кредитора, поданное после определенного срока.

Вероятности использования каждого из положений соответственно равны 0,9; 0,96; 0,99. Найти вероятность того, что дело о банкротстве фирмы возбуждено на основе второго положения.

3.18.Число грузовых автомобилей, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых автомобилей, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовой автомобиль, равна 0,1, для легковых автомобилей эта вероятность равна 0,2. К бензоколонке подъезжает для заправки автомобиль. Найти вероятность того, что это грузовой автомобиль.

3.19.Изделие проверяется на стандартность однимиз двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед.

3.20.Расследуются причины банкротства фирмы, о котором можно высказать четыре предположения (гипотезы) Н₁, Н₂, Н₃, Н₄. По статистическим данным Р(Н₁)=0,2; Р(Н₂)=0,4; Р(Н₃)=0,3; Р(Н₄)=0,1. В ходе анализа обнаружено, что фирма обанкротилась в связи с неудачной маркетинговой политикой (событие А). Условные вероятности события согласно той же статистики равны: Р(А׀Н₁)=0,9; Р(А׀Н₂)=0; Р(А׀Н₃)=0,2; Р(А׀Н₄)=0,3. Какая из гипотез наиболее вероятна при данных условиях?

3.21.Два из трех работающих телевизоров, которые работают независимо друг от друга, отказали. Найти вероятность того, что отказали первый и второй телевизоры, если вероятность отказа первого, второго и третьего телевизоров соответственно равны 0,2; 0,4 и 0,3.

3.22.Контрольные студентов-заочников попадают для проверки к одному из двух преподавателей. Вероятность того, что контрольная попадет к первому преподавателю, равна 0,6, а ко второму – 0,4. Вероятность того, что работа будет зачтена первым преподавателем, равна 0,94, а вторым – 0,98. Работа при проверке была зачтена. Найти вероятность того, что ее проверил первый преподаватель.

3.23.Число студентов, изучающих французский язык, относится к числу студентов, изучающих английский язык как 3:7. Вероятность того, что за границу на практику отправят студентов, изучающих французский язык, равна 0,2. Для студентов, изучающих английский язык, эта вероятность равна 0,5. За границу отправили студентов. Найти вероятность того, что эти студенты изучают французский язык.

3.24.Имеются две партии обуви, причем известно, что в одной партии вся обувь доброкачественная, а во второй – ¼ имеет брак. Пара обуви, взятая из наудачу выбранной партии, оказалась доброкачественной. Определить вероятность того, что вторая пара обуви из этой же партии будет иметь брак, если первая пара обуви после проверки возвращена в партию.

3.25.Исследуется динамика курсов валют А и В (по отношению к некоторой валюте С) с целью прогнозирования. Статистика валютных торгов показывает, что курс В возрастает в 90% случаев, если вырос курс А; в 60% случаев, если курс А не изменился. Предполагая, что все три исходные гипотезы об изменении курса А равновозможны, оценить вероятность этих гипотез, если известно, что на последних торгах курс В вырос.

3.26.В филиале банка А (в банке два филиала) проводят 40% всех операций этого банка, а в филиале банка В – 60%. В среднем 9 операций из 1000 проведенных в филиале банка А оказываются не прибыльными, а в филиале В – 2 операции из 500. Некоторая операция, выбранная случайным образом, оказалась не прибыльной для этого банка. Какова вероятность того, что она производилась в филиале В?

3.27.Количество банкнот, поступивших в отделение банка из четырех магазинов, соотносится как 4:3:2:1. Среди поступивших банкнот из первого магазина 0,1% банкнот в силу изношенности подлежат замене, из второго магазина таких банкнот 0,2%, из третьего – 0,25%, из четвертого – 0,5%. Наугад взятая контролером банкнота не подлежит замене. Какова вероятность того, что контролер взял банкноту, поступившую из первого магазина?

3.28.В филиале сбербанка клиенты срочных вкладов распределяются по трем категориям: первая – срок сбережения от 1 до 3 лет, вторая – срок сбережения от 3 до 5 лет, третья – срок сбережения свыше 5 лет. На 100 срочных вкладов к первой категории относится 55 вкладчиков, ко второй – 35, к третьей – 10. В среднем 8 вкладчиков из 1000 первой категории закрывают вклады, нарушив условия договора размещения денег, т.е. снимают деньги раньше обусловленного срока – 1 года; среди вкладчиков второй категории нарушителей 2 из 100, в третьей категории каждый пятый. Вкладчик закрыл вклад, нарушив условия договора размещения денег. Какова вероятность того, что вкладчик относится к клиентам третьей категории?

3.29.Число граждан, имеющих высшее образование, обратившихся на биржу труда с тем, чтобы найти работу, относится к числу граждан, имеющих среднее специальное образование, так же обратившихся на биржу труда, как 2:3. Вероятность того, что работу получит гражданин со средним специальным образованием, равна 0,1; а для гражданина с высшим образованием эта вероятность равна 0,2. Человек получил работу. Найти вероятность того, что это человек со средним специальным образованием.

3.30.На распродажу поступает в среднем 50% продукции фирмы К, 30% – фирмы Н и 20% – фирмы М. Вероятность полной продажи товаров фирмы К равна 0,7, для фирм Н и М эти вероятности соответственно равны 0,8 и 0,9. Покупатель, попавший на распродажу, покупает товар. Найти вероятность того, что этот человек купил товар фирмы К.

Случайные величины

Пусть (Ω, F, Р) – произвольное вероятностное пространство. Случайной величиной Х называется измеримая функция 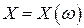, отображающая Ω в множество действительных чисел R, и такая, что при любом 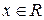множество тех 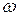,для которых 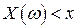, принадлежит 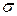-алгебре событий данного эксперимента (множества { 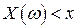} – это события).

Функцией распределения случайной величины Х называется функция F(x) действительного переменного х, определяющая вероятность того, что случайная величина Х примет в результате реализации эксперимента значение, меньшее некоторого фиксированного числа х:

.

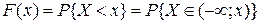Функция распределения имеет следующие свойства:

1.

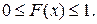
2. F(x) – неубывающая функция.

3.

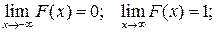
4. F(x) – непрерывна слева, т.е.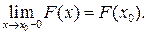

Для любых х₁ и х₂ вероятность неравенства 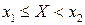вычисляется по формуле:

.

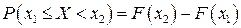Различают дискретные и непрерывные случайные величины.