Приложения производной функции в геометрии и физике
Уравнения касательной и нормали к графику функции
Пусть дана некоторая кривая 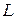 . Возьмем на кривой фиксированную точку
. Возьмем на кривой фиксированную точку 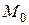 и произвольную точку
и произвольную точку 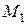 . Прямая
. Прямая 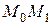 называется секущей. Предельное положение секущей
называется секущей. Предельное положение секущей 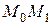 (если оно существует) при
(если оно существует) при 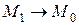 называется касательной к кривой L в точке
называется касательной к кривой L в точке 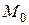 .
.
Рассмотрим функцию 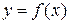 . Пусть в точке
. Пусть в точке 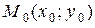 проведена касательная к графику функции. Составим уравнение касательной, проведенной в точке
проведена касательная к графику функции. Составим уравнение касательной, проведенной в точке 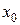 .
.
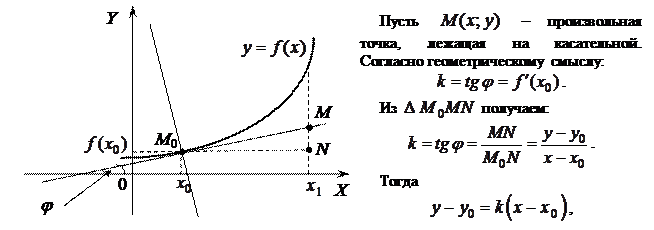
или 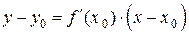 .
.
В результате получаем
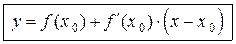 . (3.5)
. (3.5)
Равенство (3.5) есть уравнение касательной к графику функции 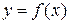 в точке
в точке 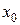 .
.
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.
Так как нормаль перпендикулярна касательной, то ее угловой коэффициент
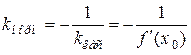 .
.
Поэтому уравнение нормали имеет вид:
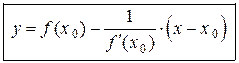 . (3.6)
. (3.6)
Пример 3.11. Составить уравнение касательной и нормали к графику функции 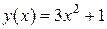 в точке
в точке 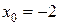 .
.
Решение. Для составления уравнения касательной воспользуемся формулой (3.5). Находим:
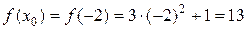 .
.
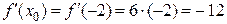 .
.
Тогда
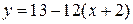 или
или 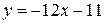 .
.
Для составления уравнения нормали воспользуемся формулой (3.6).
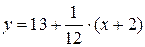 или
или 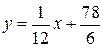 . ,
. ,
Производная функции в физике
Согласно механическому смыслу: скорость прямолинейного движения материальной точки в момент времени  есть первая производная от пути
есть первая производная от пути 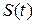 по времени
по времени  , т.е.
, т.е.
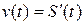 .
.
А вторая производная от пути по времени или первая производная от скорости есть ускорение прямолинейного движения материальной точки, т.е.
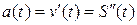 .
.
Если другие физические процессы заданы в виде функции 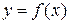 , то
, то 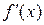 − есть скорость протекания этого процесса.
− есть скорость протекания этого процесса.
Пример 3.12. Закон движения тела имеет вид: 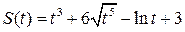 (м). Найти:
(м). Найти:
1) скорость и ускорение движения тела в момент время 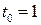 с;
с;
2) кинетическую энергию тела через 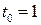 с после начала движения, если его масса
с после начала движения, если его масса 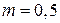 кг (ответ записать в кДж).
кг (ответ записать в кДж).
Решение. 1) Согласно механическому смыслу 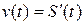 . Сначала находим скорость тела в общем виде, а потом значение скорости в момент времени
. Сначала находим скорость тела в общем виде, а потом значение скорости в момент времени 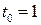 с:
с:
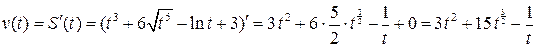 ;
;
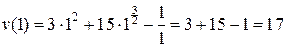 (м/с).
(м/с).
Далее находим ускорение тела в общем виде и значение ускорения в момент времени  с:
с:
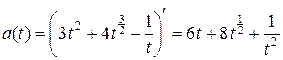 ;
;
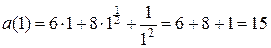 (м/с2).
(м/с2).
2) Кинетическая энергия тела находится по следующей формуле:
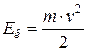 .
.
Находим кинетическую энергию тела в момент времени 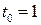 с:
с:
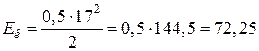 (Дж)
(Дж) 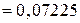 (кДж).
(кДж).
,
4. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Понятие дифференциала функции,
Его геометрический смысл
Пусть дана функция 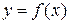 , определенная на множестве X, и в точке
, определенная на множестве X, и в точке 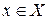 имеет отличную от нуля производную, т.е.
имеет отличную от нуля производную, т.е. 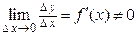 . Тогда по теореме о связи функции, ее предела и б.м.ф., можно записать
. Тогда по теореме о связи функции, ее предела и б.м.ф., можно записать 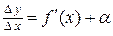 , где
, где 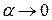 при
при 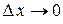 , или
, или 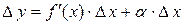 .
.
Таким образом, приращение функции 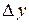 представляет собой сумму двух слагаемых
представляет собой сумму двух слагаемых 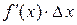 и
и 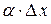 , являющиеся бесконечно малыми при
, являющиеся бесконечно малыми при 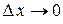 . При этом первое слагаемое есть бесконечно малая функция одного порядка с
. При этом первое слагаемое есть бесконечно малая функция одного порядка с 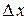 , так как
, так как 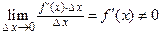 , а второе слагаемое есть бесконечно малая функция более высокого порядка, чем
, а второе слагаемое есть бесконечно малая функция более высокого порядка, чем 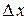 , так как
, так как 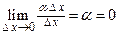 .
.
Слагаемое 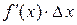 называют главной частью приращения функции
называют главной частью приращения функции 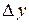 .
.
Определение 4.1. Дифференциалом функции 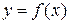 в точке x называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
в точке x называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается 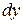 (или
(или 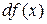 ):
):
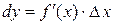 . (4.1)
. (4.1)
Дифференциал 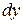 называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной x, т.е. дифференциал функции
называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной x, т.е. дифференциал функции 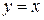 . Так как
. Так как 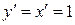 , то согласно формуле (2.1), имеем
, то согласно формуле (2.1), имеем 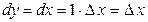 , т.е. дифференциал независимой переменной равен приращению этой переменной:
, т.е. дифференциал независимой переменной равен приращению этой переменной: 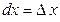 . Поэтому формулу (2.1) можно записать так:
. Поэтому формулу (2.1) можно записать так:
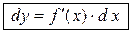 , (4.2)
, (4.2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (4.2) следует равенство 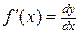 . Теперь обозначение производной можно рассматривать как отношение дифференциалов
. Теперь обозначение производной можно рассматривать как отношение дифференциалов 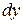 и
и 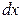 .
.
Пример 4.1. Найти дифференциал функции
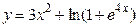
а) в общем виде;
б) в точке 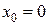 ;
;
в) при 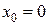 и
и 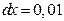 .
.
Решение. Находим производную первого порядка:
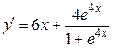 .
.
а) Используя формулу (4.2), получаем
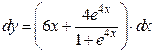 .
.
б) Дифференциал функции в точке равен
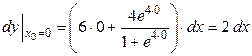 .
.
в) При 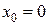 и
и 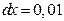 получаем:
получаем:
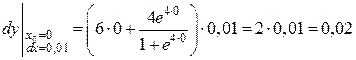 .
.
,
Выясним геометрический смысл дифференциала функции.
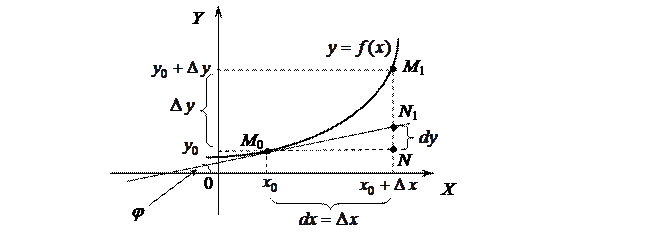
Проведем к графику функции 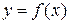 в точке
в точке 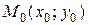 касательную
касательную 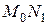 и рассмотрим ординату этой касательной для точки
и рассмотрим ординату этой касательной для точки 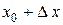 . На рисунке
. На рисунке 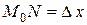 ,
, 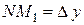 . Из прямоугольного треугольника
. Из прямоугольного треугольника 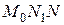 имеем:
имеем:
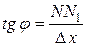 , т.е.
, т.е. 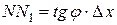 .
.
Но, согласно геометрическому смыслу производной, 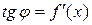 . Поэтому
. Поэтому 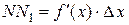 .
.
Сравнивая полученный результат с формулой (2.1.), получаем 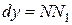 .
.
Геометрический смысл: дифференциал функции 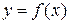 в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение
в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение 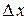 .
.
Правила вычисления дифференциала аналогичны соответствующим правилам нахождения производной.
Инвариантность формы записи дифференциала
Пусть 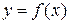 для
для 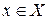 , тогда
, тогда
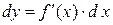 .
.
Рассмотрим сложную функцию 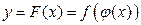 , где
, где 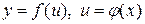
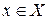 , причем
, причем 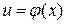 и
и 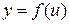 дифференцируемы соответственно в точках x и
дифференцируемы соответственно в точках x и 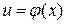 . Тогда
. Тогда 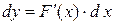 , но
, но 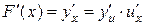 следовательно,
следовательно, 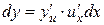 . А так как
. А так как 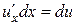 , то
, то
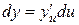 .
.
Таким образом, форма записи дифференциала сохраняется, если независимую переменную заменить некоторой функцией. Это свойство называется инвариантностью (неизменностью) формы записи дифференциала.
Заметим, что из инвариантности следует, что, хотя 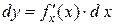 (x – независимая переменная), а
(x – независимая переменная), а 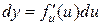 (
( 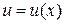 – функция), запись их одинакова. Однако сущность этих формул различна:
– функция), запись их одинакова. Однако сущность этих формул различна: 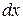 задается произвольно,
задается произвольно, 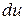 же задавать произвольно, вообще говоря, нельзя;
же задавать произвольно, вообще говоря, нельзя; 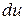 нужно вычислить по формуле дифференциала
нужно вычислить по формуле дифференциала 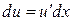 . Это относится и к случаю с несколькими промежуточными функциями.
. Это относится и к случаю с несколькими промежуточными функциями.
