Пункт 4. Приложения производной
Функция 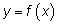 называется возрастающей на интервале
называется возрастающей на интервале 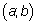 , если для любых x1 и x2 из этого интервала, для которых
, если для любых x1 и x2 из этого интервала, для которых 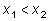 , верно неравенство
, верно неравенство 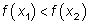 .
.
Функция 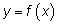 называется убывающей на интервале
называется убывающей на интервале 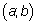 , если для любых x1 и x2 из этого интервала, для которых
, если для любых x1 и x2 из этого интервала, для которых 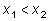 , верно неравенство
, верно неравенство 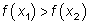 .
.
Необходимое условие возрастания функции. Если функция 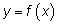 дифференцируема и возрастает на интервале
дифференцируема и возрастает на интервале 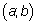 , то
, то 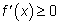 для всех
для всех 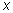 из этого интервала.
из этого интервала.
Необходимое условие убывания функции. Если функция 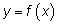 дифференцируема и убывает на интервале
дифференцируема и убывает на интервале 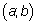 , то
, то 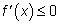 для всех
для всех 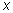 из этого интервала.
из этого интервала.
Достаточное условие возрастания (убывания функции). Пусть функция 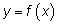 дифференцируема на интервале
дифференцируема на интервале 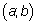 . Если во всех точках этого интервала
. Если во всех точках этого интервала 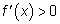 , то функция возрастает на этом интервале, а если
, то функция возрастает на этом интервале, а если 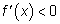 , то функция убывает на этом интервале.
, то функция убывает на этом интервале.
Точка x = x0 называется точкой максимума, а число 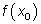 — максимумом функции, если для всех точек из некоторой окрестности точки x0 , не совпадающих с x0 , выполняется неравенство
— максимумом функции, если для всех точек из некоторой окрестности точки x0 , не совпадающих с x0 , выполняется неравенство 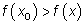 .
.
Точка x = x0 называется точкой минимума, а число 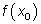 — минимумом функции, если для всех точек из некоторой окрестности точки x0 , не совпадающих с точкой x0 , выполняется неравенство
— минимумом функции, если для всех точек из некоторой окрестности точки x0 , не совпадающих с точкой x0 , выполняется неравенство 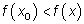 .
.
Точки максимума и минимума называются точками экстремума.
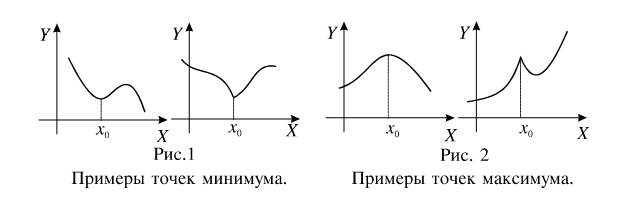
Необходимое условие существования экстремума
Если x0 — точка экстремума, то производная в этой точке равна нулю или не существует.
Достаточное условие существования экстремума
Если функция 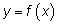 непрерывна в точке x = x0 , дифференцируема в некоторой окрестности этой точки, и при переходе через точку x0 производная
непрерывна в точке x = x0 , дифференцируема в некоторой окрестности этой точки, и при переходе через точку x0 производная 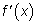 меняет знак, то x = x0 — точка:
меняет знак, то x = x0 — точка:
а) 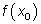 — максимум, если
— максимум, если 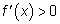 , при
, при 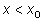 и
и 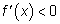 , при
, при 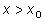 .
.
б) 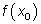 — минимум, если
— минимум, если 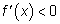 , при
, при 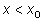 и
и 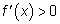 , при
, при 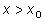 .
.
Число 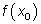 называется наибольшим значением функции на отрезке
называется наибольшим значением функции на отрезке 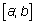 , если для всех
, если для всех 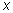 из этого отрезка выполняется неравенство
из этого отрезка выполняется неравенство 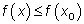 ; число называется наименьшим значением функции на отрезке
; число называется наименьшим значением функции на отрезке 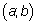 , если для всех
, если для всех 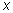 из этого отрезка выполняется неравенство
из этого отрезка выполняется неравенство 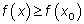 .
.
Функция принимает свое наибольшее или наименьшее значение в точках экстремума или на границе. Для нахождения наибольшего и наименьшего значений функции на отрезке руководствуются следующим правилом: находят все критические точки функции (производная равна нулю), лежащие внутри отрезка, и находят значения функции в этих точках и на концах отрезка. Наибольшее из этих значений будет наибольшим, а наименьшее из этих значений — наименьшим значением функции на отрезке.
Пример.
27.Найти наименьшее и наибольшее значение функции: 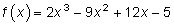 на отрезке
на отрезке 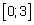 .
.
Решение.
Находим 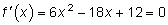 и приравниваем к нулю:
и приравниваем к нулю: 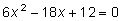 или
или 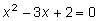 .
.
Решая уравнение, находим критические точки 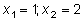 , причем обе лежат внутри отрезка.
, причем обе лежат внутри отрезка.
Находим значение функции 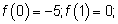
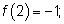
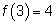 . Наибольшее значение равно 4, а наименьшее -5.
. Наибольшее значение равно 4, а наименьшее -5.
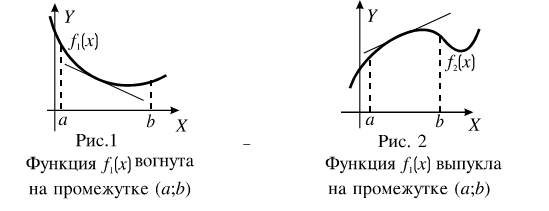
Если график функции 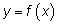 имеет касательную в точке x = x0 , и в некоторой окрестности этой точки он лежит ниже касательной, то он называется выпуклым в точке x0 ; a если в некоторой окрестности этой точки он лежит выше касательной, то он называется вогнутым.
имеет касательную в точке x = x0 , и в некоторой окрестности этой точки он лежит ниже касательной, то он называется выпуклым в точке x0 ; a если в некоторой окрестности этой точки он лежит выше касательной, то он называется вогнутым.
График 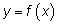 называется выпуклым (вогнутым) на интервале
называется выпуклым (вогнутым) на интервале 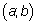 , если он выпуклый (вогнутый) в каждой точке этого интервала.
, если он выпуклый (вогнутый) в каждой точке этого интервала.
Достаточное условие выпуклости (вогнутости) графика функции. Если функция 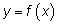 дважды дифференцируема на интервале
дважды дифференцируема на интервале 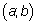 и для каждого
и для каждого 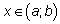
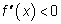
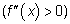 , то график функции
, то график функции 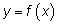 является выпуклым (вогнутым) на этом интервале.
является выпуклым (вогнутым) на этом интервале.
Точка 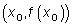 называется точкой перегиба графика функции
называется точкой перегиба графика функции 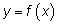 , если в этой точке существует касательная и это точка отделяет интервал выпуклости от интервала вогнутости.
, если в этой точке существует касательная и это точка отделяет интервал выпуклости от интервала вогнутости.
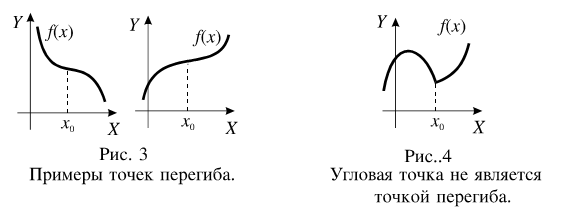
Необходимое условие точки перегиба. Если x = x0 — точка перегиба графика функции 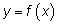 , то
, то 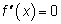 или не существует.
или не существует.
Достаточные условия точки перегиба. Если функция 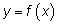 дважды дифференцируема, график этой функции имеет в этой точке касательную и при переходе через эту точку
дважды дифференцируема, график этой функции имеет в этой точке касательную и при переходе через эту точку 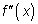 меняет знак, то x0 — точка перегиба графика функции
меняет знак, то x0 — точка перегиба графика функции 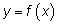 .
.
Асимптотой данной кривой называется такая прямая, при которой расстояние от точки на кривой до этой прямой стремится к нулю, при неограниченном удалении точки на кривой от начала координат.
Прямая x = x0 является вертикальной асимптотой, если 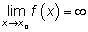 .
.
Уравнение наклонной асимптоты имеет вид
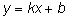 , где
, где 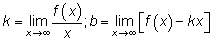 .
.
План исследования функции
Если требуется построить график функции 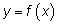 , то надо предварительно исследовать эту функцию. Для исследования рекомендуется следующий план:
, то надо предварительно исследовать эту функцию. Для исследования рекомендуется следующий план:
1) найти область определения 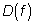 ;
;
2) найти точки разрыва, вертикальные асимптоты;
3) найти асимптоты;
4) найти точки пересечения графика с осями координат;
5) определить четность 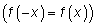 или нечетность
или нечетность 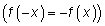 , т.е. является ли график этой функции симметричным относительно оси ординат, или начала координат, или же такой симметрии нет;
, т.е. является ли график этой функции симметричным относительно оси ординат, или начала координат, или же такой симметрии нет;
6) найти экстремумы, интервалы возрастания и убывания;
7) найти точки перегиба, интервалы выпуклости и вогнутости. На основании этого исследования строится график функции.
Если в каких-то местах ход графика остается неясным, то находят дополнительные точки на этом графике.
Пример.
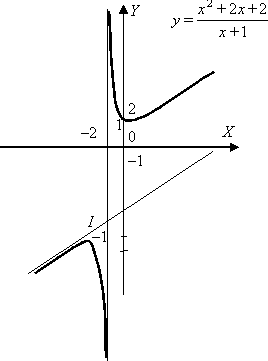
28.Исследовать функцию 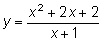 и построить ее график.
и построить ее график.
Решение:
1. 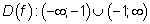
2. Точка разрыва 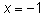 , вертикальная асимптота
, вертикальная асимптота 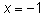 .
.
3. Найдем невертикальную асимптоту 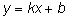 .
.
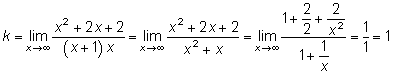
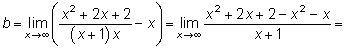
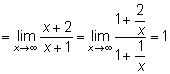
Итак, уравнение невертикальной асимптоты 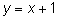 .
.
4. При 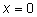 находим точку пересечения с осью ординат
находим точку пересечения с осью ординат 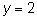 . При
. При 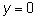 получаем уравнение
получаем уравнение 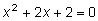 . Это уравнение не имеет решений
. Это уравнение не имеет решений 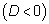 , следовательно, график не имеет пересечения с осью абсцисс .
, следовательно, график не имеет пересечения с осью абсцисс .
5. Проверим, является ли функция четной или нечетной.
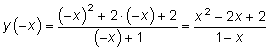
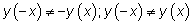
Функция не является ни четной, ни нечетной, поэтому у ее графика нет симметрии ни относительно оси ординат, ни относительно начала координат.
6. Найдем точки экстремума и интервалы возрастания и убывания функции.
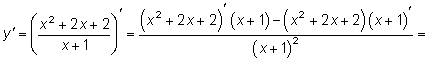
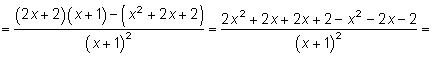
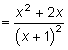
Найдем критические точки, приравняв производную нулю:
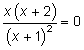
Критические точки 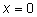 и
и 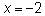 . Эти точки разбивают область определения функции на четыре интервала. Рассмотрим результат исследования в таблице.
. Эти точки разбивают область определения функции на четыре интервала. Рассмотрим результат исследования в таблице.
| х | (– 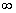 ;-2) ;-2) | –2 | (–2;–1) | (–1;0) | (0;+ 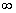 ) ) | |
| y' | + | – | – | + | ||
| y | возрастает | max | убывает | убывает | min | возрастает |
7. Определим интервалы выпуклости, вогнутости и точки перегиба.
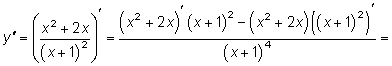
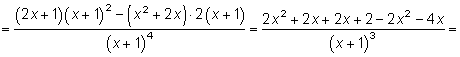
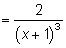
Итак, 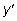 не обращается в нуль ни в одной точке, следовательно, точек перегиба нет. Построим таблицу:
не обращается в нуль ни в одной точке, следовательно, точек перегиба нет. Построим таблицу:
| х | (– 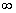 ;–1) ;–1) | (–1;+ 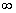 ) ) |
| y' | – | + |
| y | 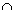 | 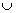 |
Занесем все данные в одну общую таблицу:
| х | (– 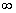 ;–2) ;–2) | –2 | (–2;–1) | (–1;0) | (–1;+ 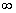 ) ) | |
| y' | + | – | – | + | ||
| y' | – | – | + | + | ||
| y | возрастает 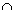 | max –2 | убывает 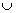 | убывает 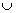 | min 2 | возрастает  |
Учитывая проведенное исследование, построим график: