Дифференциалы высших порядков
Пусть  дифференцируемая функция, а ее аргумент x – независимая переменная. Ее первый дифференциал
дифференцируемая функция, а ее аргумент x – независимая переменная. Ее первый дифференциал 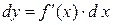 есть также функция x. Можно найти дифференциал этой функции.
есть также функция x. Можно найти дифференциал этой функции.
Дифференциалом второго порядка называется дифференциал от первого дифференциала, т.е.
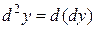 .
.
Найдем выражение второго дифференциала функции  . Так как
. Так как 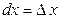 не зависит от x, то при дифференцировании считаем
не зависит от x, то при дифференцировании считаем 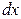 постоянным:
постоянным:
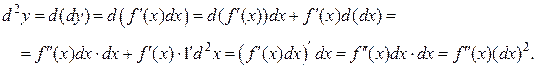
Таким образом, получаем
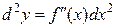 . (4.3)
. (4.3)
Равенство (4.3) есть формула, по которой находится дифференциал второго порядка функции  , если x – независимая переменная.
, если x – независимая переменная.
Аналогично определяется и находится дифференциал третьего порядка:
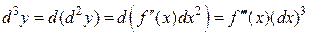 .
.
И, вообще, дифференциал n-го порядка есть дифференциал от дифференциала (n-1)-го порядка: 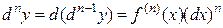 .
.
Отсюда находим, что 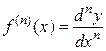 . В частности, при
. В частности, при 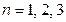 соответственно получаем:
соответственно получаем:
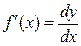 ,
, 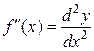 ,
, 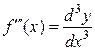 .
.
т.е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.
Отметим, что все приведенные выше формулы справедливы только, если x – независимая переменная. Если же функцию  , где x есть функция от какой-то другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.
, где x есть функция от какой-то другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.
Используя формулу дифференциала произведения ( 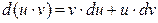 ), получаем:
), получаем:
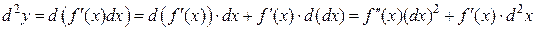 ,
,
т.е.
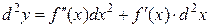 . (4.4)
. (4.4)
Сравнивая формулы (2.3) и (2.4), убеждаемся, что в случае сложной функции формула дифференциала второго порядка изменяется: появляется второе слагаемое 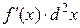 .
.
Ясно, что если x – независимая переменная, то
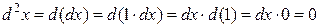
и формула (4.4) переходит в формулу (4.3).
5. ИССЛЕДОВАНИЕ ФУНКЦИЙ
С ПОМОЩЬЮ ПРОИЗВОДНЫХ
Возрастание и убывание функций.
Точки экстремума
| В мире не происходит ничего, в чем бы не был виден смысл какого-нибудь максимума или минимума. Л. Эйлер |
Процессы, происходящие в механике, физике, химии, термодинамике, экономике, очень часто описываются функциями, заданными формулами. Чтобы знать характеристики рассматриваемого процесса, следует изучить характеристики функций, описывающих процесс, а для наглядности рассмотреть функции в их графическом задании. Но чаще интерес представляет не графическое задание функции, а качественное поведение графика функции без соблюдения масштабных размеров для достаточно точного (приближенного с заданной точностью) определения значений функции. Эти качественные свойства функций можно описать, используя методы дифференциального исчисления.
Теорема 5.1 (условие монотонности функции). Пусть функция 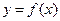 определена на X и внутри имеет конечную производную
определена на X и внутри имеет конечную производную 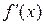 . Для того чтобы
. Для того чтобы 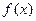 была монотонно возрастающей (убывающей), достаточно, чтобы
была монотонно возрастающей (убывающей), достаточно, чтобы 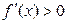 (
( 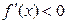 ) для всех x внутри X.
) для всех x внутри X.
Теорему примем без доказательства.
Если функция 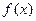 , определенная и непрерывная на множестве X, не является монотонной, то найдутся такие части промежутка X, что наибольшее или наименьшее значение достигается функцией во внутренней точке.
, определенная и непрерывная на множестве X, не является монотонной, то найдутся такие части промежутка X, что наибольшее или наименьшее значение достигается функцией во внутренней точке.
Определение 5.1. Функция 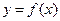 имеет в точке
имеет в точке  максимум (минимум), если существует такая окрестность точки
максимум (минимум), если существует такая окрестность точки 
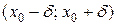 , не выходящая из области определения функции, что для всех
, не выходящая из области определения функции, что для всех 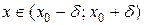
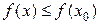
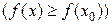 .
.
Максимум и минимум называют общим термином «экстремум».
Из определения экстремума следует, что вне окрестности точки максимума  значения функции могут быть больше этого максимума. Поэтому такой максимум называется локальным (местным). Аналогично определяется локальный минимум. Точки локального максимума и минимума называются точками локального экстремума, а значения функции в них – локальными экстремумами функции.
значения функции могут быть больше этого максимума. Поэтому такой максимум называется локальным (местным). Аналогично определяется локальный минимум. Точки локального максимума и минимума называются точками локального экстремума, а значения функции в них – локальными экстремумами функции.
Если функция 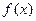 определена на отрезке
определена на отрезке 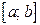 и имеет локальный экстремум на каком-то из концов этого отрезка, то такой экстремум будем называть локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для a и левой для b полуокрестностью.
и имеет локальный экстремум на каком-то из концов этого отрезка, то такой экстремум будем называть локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для a и левой для b полуокрестностью.

Рассмотрим условия существования экстремума функции. Необходимое условие экстремума примем без доказательства.
Теорема 5.2 (необходимое условие экстремума). Если дифференцируемая функция 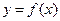 имеет экстремум в точке
имеет экстремум в точке  , то ее производная в этой точке равна нулю:
, то ее производная в этой точке равна нулю: 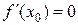 .
.
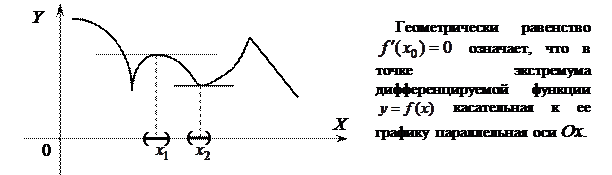
Отметим, что обратная теорема неверна, т.е. если 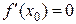 , то это не значит, что
, то это не значит, что  – точка экстремума.
– точка экстремума.
Точки, в которых производная равна нулю, называются стационарными (критическими или «подозрительными» на экстремум). Точки, в которых функция непрерывна, но производная не существует или бесконечна, также являются критическими, так как это тоже точки, где может быть экстремум.
Например, для функции 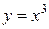 ее производная
ее производная 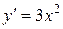 равна нулю при
равна нулю при 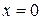 , но
, но 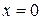 не является точкой экстремума. Непрерывная функция
не является точкой экстремума. Непрерывная функция 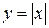 в точке
в точке 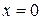 производной не имеет, но точка
производной не имеет, но точка 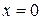 – точка минимума.
– точка минимума.
Теорема 5.3 (первое достаточное условие экстремума). Пусть точка  – критическая, т.е.
– критическая, т.е. 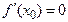 или
или 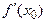 не существует. Предположим, что в некоторой окрестности
не существует. Предположим, что в некоторой окрестности 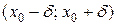 для
для 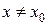 существует конечная производная
существует конечная производная 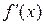 и она сохраняет свой знак слева и справа от
и она сохраняет свой знак слева и справа от  . Тогда:
. Тогда:
1) если 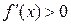 при
при 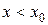 и
и 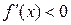 при
при 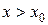 , т.е. при переходе через
, т.е. при переходе через  производная изменяет знак с «+» на «-», то в точке
производная изменяет знак с «+» на «-», то в точке  функция
функция 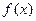 имеет максимум;
имеет максимум;
2) если 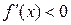 при
при 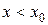 и
и 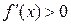 при
при 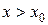 , т.е. при переходе через
, т.е. при переходе через  производная изменяет знак с «-» на «+», то в точке
производная изменяет знак с «-» на «+», то в точке  функция имеет минимум;
функция имеет минимум;
3) если при переходе через  знак производной
знак производной 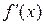 не изменяется, то экстремума в точке
не изменяется, то экстремума в точке  нет.
нет.
Теорема 5.4 (второе достаточное условие экстремума). Если  – критическая точка, т.е.
– критическая точка, т.е. 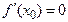 , и функция
, и функция 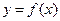 в точке
в точке  имеет вторую производную
имеет вторую производную 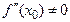 , то в случае
, то в случае 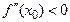 функция имеет в точке
функция имеет в точке  максимум, а при
максимум, а при 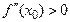 – минимум.
– минимум.
Надо отметить, что т. 4.4. не применима, если 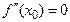 или
или 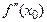 не существует.
не существует.
Пример 5.1. Найти точки экстремума и промежутки возрастания и убывания для функции:
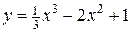 .
.
Решение. Функция определена и дифференцируема на 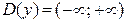 . Ее производная равна
. Ее производная равна 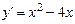 . Необходимое условие экстремума:
. Необходимое условие экстремума: 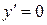 . Имеем
. Имеем 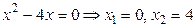 . Получили две критические точки, которые разбивают всю область определения на три интервала
. Получили две критические точки, которые разбивают всю область определения на три интервала 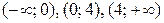 . Применим первое достаточное условие экстремума, т.е. на рисунке отметим знаки первой производной и стрелками поведение функции на каждом интервале
. Применим первое достаточное условие экстремума, т.е. на рисунке отметим знаки первой производной и стрелками поведение функции на каждом интервале
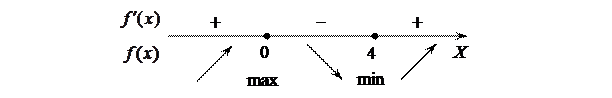
Точка 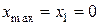 – точка максимума.
– точка максимума. 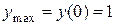 .
.
Точка 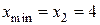 – точка минимума.
– точка минимума. 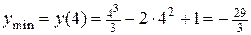 .
.
На интервалах 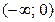 и
и 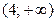
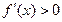 , следовательно, функция возрастает, на интервале
, следовательно, функция возрастает, на интервале 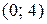 – функция убывает.
– функция убывает.
II способ.
Вместо исследования перемены знака первой производной можно найти значения второй производной в критических точках: 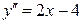 .
. 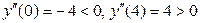 , т.е. в точке
, т.е. в точке 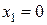 вторая производная отрицательна, то в этой точке функция имеет максимум, а если в точке
вторая производная отрицательна, то в этой точке функция имеет максимум, а если в точке 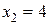 вторая производная положительна, то в этой точке функция имеет минимум. ,
вторая производная положительна, то в этой точке функция имеет минимум. ,
