Матричный способ решения систем.

Рассмотрим систему трех уравнений с тремя неизвестными:

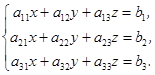
Введем следующие обозначения:

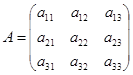– матрица коэффициентов системы

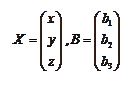
– столбец неизвестных и столбец свободных членов, соответственно.

Тогда систему можно записать в матричной форме:

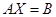
Пусть матрица 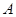имеет обратную матрицу .

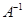Умножим матричное уравнение на 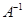,получим

.

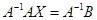Заметив, что 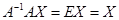, получим

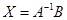-решение матричного уравнения.

Переходя к координатной записи в последнем равенстве, выпишем решение исходной системы уравнений.

Построение обратной матрицы

Обратная матрица существует только для квадратной матрицы, определитель которой не равен нулю. Такая матрица называется невырожденной.

Пусть матрица 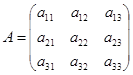- невырождена, т.е.

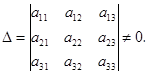
Построим союзную матрицу 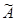, которая составлена из алгебраических дополнений элементов матрицы 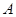, причём в столбцах матрицы 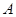записываются алгебраические дополнения соответствующих строк этой матрицы.

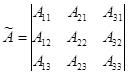, где

.

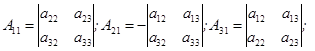
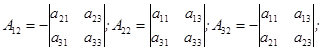
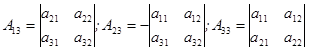Обратная матрица 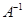имеет вид

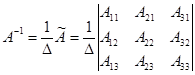
Решим систему (см. пример 1) матричным способом.

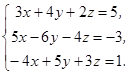
Здесь

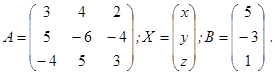
Решим матричное уравнение .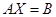

Составим обратную матрицу .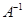

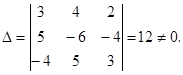
Выпишем все алгебраические дополнения для данной матрицы.

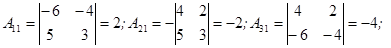
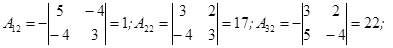
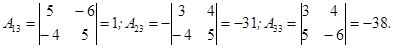
Составим матрицу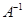

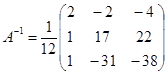
Решим матричное уравнение

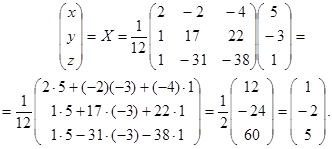
Отсюда получаем решение системы:

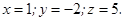
Ответ: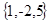

Замечание.

Аналогично, матричным способом, можно решать любые системы 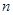уравнений с 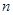неизвестными, если только определитель системы не равен нулю.

Контрольная работа №1 по теме

«Элементы линейной и векторной алгебры»

1.1. Вычислить определитель.

1.1.1.		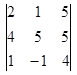1.1.2		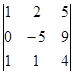1.1.3.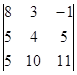
1.1.4.		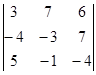1.1.5		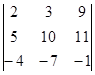1.1.6.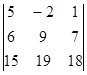
1.1.7.		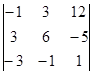1.1.8		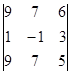1.1.9.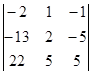
1.1.10.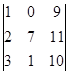

1.2. Решить систему трех уравнений с тремя неизвестными тремя способами: методом Гаусса, по формулам Крамера и матричным способом.

1.2.1.		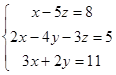1.2.2.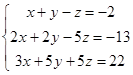
1.2.3.		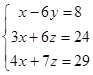1.2.4.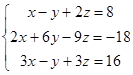
1.2.5.		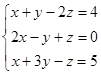1.2.6.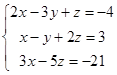
1.2.7.		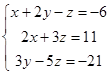1.2.8.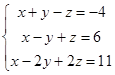
1.2.9.		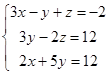1.2.10.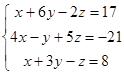

1.2. Вычислить .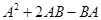

1.3.1.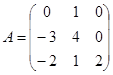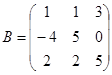
1.3.2.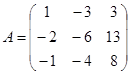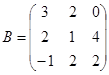
1.3.3.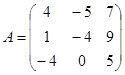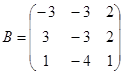
1.3.4.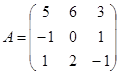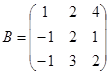
1.3.5.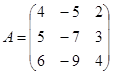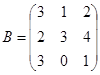
1.3.6.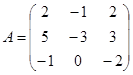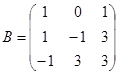
1.3.7.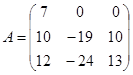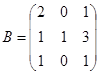
1.3.8.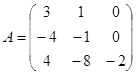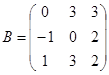
1.3.9.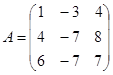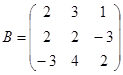
1.3.10.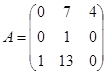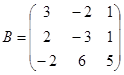

1.4. Даны векторы , , , .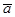

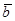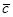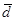1. Показать, что 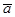, , 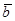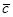образуют базис и найти координаты вектора 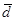в этом базисе.

2. Найти: a) ;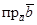

б) ;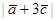

в) ;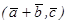

г) ;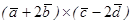

д) ;

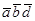е) угол между векторам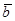и и .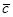

1.4.1.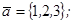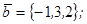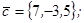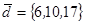
1.4.2.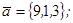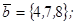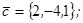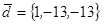
1.4.3.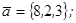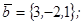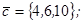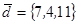
1.4.4.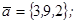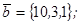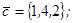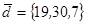
1.4.5.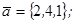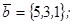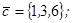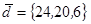
1.4.6.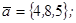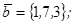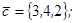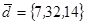
1.4.7.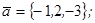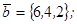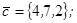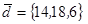
1.4.8.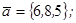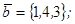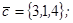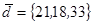
1.4.9.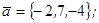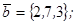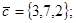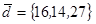
1.4.10.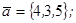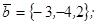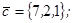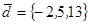

1.5. Даны точки , , ,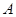

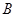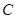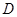
1. Показать, что точки 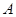, , 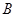, 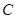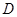не лежат в одной плоскости.

2. Вычислить: а)объем пирамиды ;

б)длину ребра ;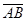

в) площадь грани ;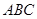

г)угол между граням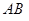и и .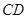

1.5.1.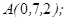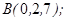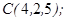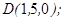
1.5.2.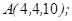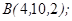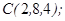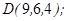
1.5.3.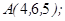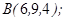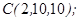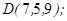
1.5.4.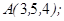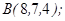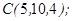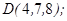
1.5.5.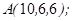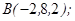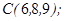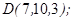
1.5.6.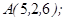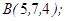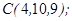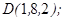
1.5.7.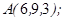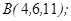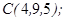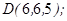
1.5.8.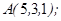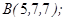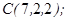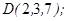
1.5.9.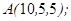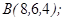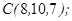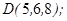
1.5.10.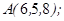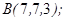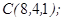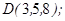

Контрольные вопросы к экзамену

1. Матрицы и действия над ними.

2. Обратная матрица.

3. Определители и их свойства, вычисление (на примере определителей третьего порядка).

4. Решение систем линейных уравнений методом Гаусса.

5. Решение систем линейных уравнений методом Крамера.

6. Решение систем линейных уравнений матричным методом.

7. Векторы, координаты вектора, модуль, направляющие косинусы.

8. Линейные операции над векторами.

9. Скалярное произведение векторов, свойства, вычисление, приложение к геометрическим задачам.

10. Векторное произведение векторов, свойства, вычисление, применение к геометрическим задачам.

11. Смешанное произведение векторов, свойства, вычисление, приложение к геометрическим задачам.