Решение систем с помощью обратной матрицы (матричный способ)

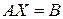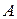Способ основан на том, что любую систему линейных уравнений можно записать в матричном виде: , где – матрица из коэффициентов при неизвестных, 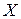– матрица-столбец из самих неизвестных, 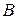– матрица-столбец из свободных членов уравнений.

Рассмотрим для примера систему 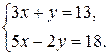. Введем матрицы 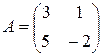, , 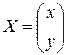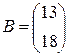. С помощью этих матриц систему можно записать так: 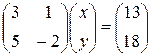. Выполнив действие в левой части равенства и используя условие равенства матриц, придем снова к исходной системе. В матричном виде можно представить и прямоугольные системы, например, систему 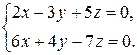можно записать так: .

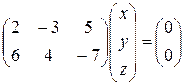Итак, всякую систему можно записать в виде матричного уравнения 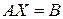. Если матрица 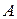в этом уравнении квадратная, то его можно решить по соответствующей формуле: .

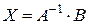Пример. Систему линейных уравнений 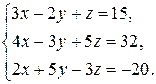решить с помощью обратной матрицы.

Выпишем матрицу коэффициентов системы 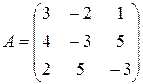и найдем для неё обратную по общей формуле: 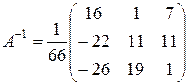. Тогда 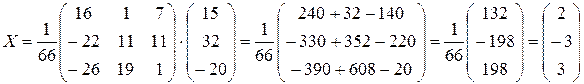. Таким образом, 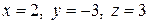. Подстановкой найденных значений во все уравнения системы убеждаемся, что оно верное.

Решение систем по формулам Крамера

Для квадратной неоднородной системы с любым числом уравнений 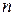неизвестную величину с номером 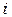можно найти по формуле:

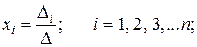
где 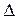– главный определитель системы;

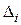– вспомогательный определитель, полученный из главного заменой коэффициентов при неизвестном 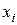на столбец свободных членов.

Анализ полученной формулы и применение ее на практике для решения систем позволяет сделать следующие выводы:

1) если главный определитель системы 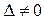, то система имеет единственное решение;

2) если 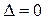, а хотя бы один из вспомогательных определителей 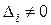, то система не имеет решения;

3) если и главный и все вспомогательные определители равны 0, то система или не имеет решения, или имеет бесконечное множество решений.

Формулы Крамера являются особенно удобными, когда коэффициенты системы не являются целыми числами.

Пример. Систему линейных уравнений 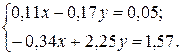решить по формулам Крамера.

Вычислим необходимые определители:

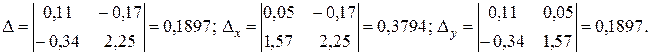Тогда .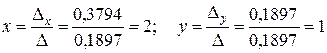

Примечание: формула и пример вычисления определителя второго порядка приведены на стр. 10.

Пример решения контрольной работы №1

Задание 1

Вычислить значение функции 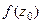, если

.

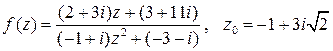Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.

Решение

Подставим значение 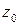в данную функцию. Выполним действия в числителе и знаменателе полученной функции, предварительно вычислив

.

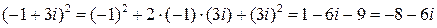Получим .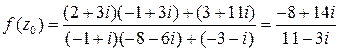

Чтобы выполнить деление комплексных чисел, помножим числитель и знаменатель на выражение, сопряженное знаменателю, то есть на (11+3i), получим

.

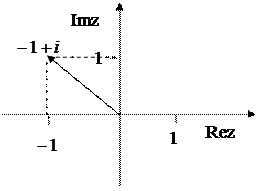
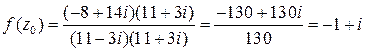Назовем число 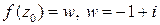. Изобразим его на комплексной плоскости:

Тригонометрическая форма комплексного числа имеет вид:

,

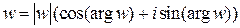где 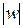– модуль комплексного числа и 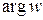– главное значение аргумента комплексного числа, его можно найти, как рассказано в пункте 1.1.1.

Для полученного комплексного числа 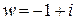,, , 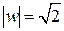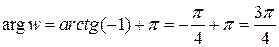. Тогда число 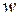в тригонометрической форме для нашего примера будет иметь вид: .

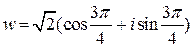Ответ: .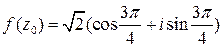

Задание 2

Найти 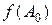, если .

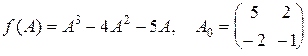Решение

Запишем 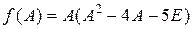, где 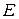– единичная матрица. Найдем 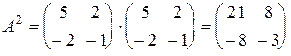, определим выражение в скобке: .

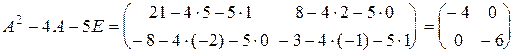Окончательно: .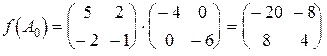

Задание 3

Найти решение системы линейных алгебраических уравнений

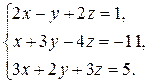
по формулам Крамера.

Для данной системы формулы Крамера имеют вид:

.

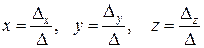Вычислим необходимые определители, используя правило треугольников (см. стр. 11, 12):

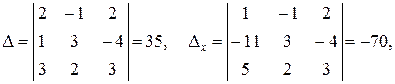
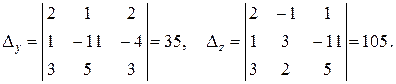
Тогда: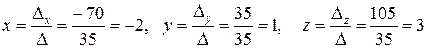

Подстановкой в систему убеждаемся, что решение верное.

Ответ: .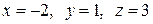

Задание 4

Пример решения этого задания приведён на страницах 15,16.