Тема: Действия над комплексными числами в тригонометрической и показательной формах
Цель: Формирование навыков выполнения действий над комплексными числами в тригонометрической и показательной формах
Время выполнения: 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Комплексными числами называются числа вида 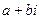 , где
, где 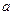 и
и 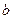 - действительные числа, а число
- действительные числа, а число 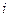 , определяемое равенством
, определяемое равенством 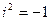 , называется мнимой единицей.
, называется мнимой единицей.
Запись комплексного числа в виде 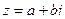 называется алгебраической формой записи комплексного числа.
называется алгебраической формой записи комплексного числа.
Представление комплексного числа в виде 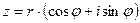 , где
, где 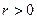 , называется тригонометрической формой записи комплексного числа.
, называется тригонометрической формой записи комплексного числа.
Произведение комплексных чисел 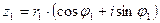 и
и 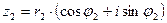 находится по формуле:
находится по формуле:
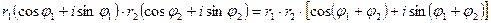 , (24.1)
, (24.1)
то есть
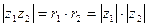 ,
, 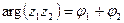 . (24.2)
. (24.2)
Таким образом, при умножении двух комплексных числе, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются.
Частное комплексных чисел 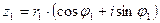 и
и 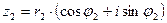 находится по формуле:
находится по формуле:
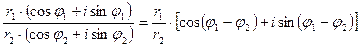 , (24.3)
, (24.3)
то есть
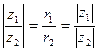 ,
, 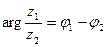 . (24.4)
. (24.4)
Таким образом, при делении комплексных чисел, заданных в тригонометрической форме, их модули делятся, аргументы вычитаются.
При возведении комплексного числа 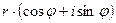 в
в 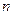 -ую степень используется формула
-ую степень используется формула
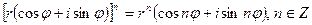 , (24.5)
, (24.5)
которая называется формулой Муавра.
Для извлечения корня 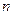 -ой степени из комплексного числа
-ой степени из комплексного числа 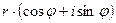 используется формула
используется формула
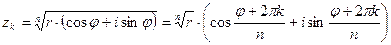 , (24.6)
, (24.6)
где 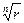 - арифметический корень,
- арифметический корень, 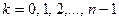 .
.
Степень 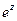 с комплексным показателем
с комплексным показателем 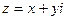 определяется равенством
определяется равенством
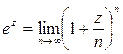 . (24.7)
. (24.7)
Можно доказать, что
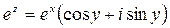 , (24.8)
, (24.8)
то есть 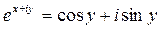 . (24.9)
. (24.9)
В частности, при 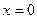 получается соотношение
получается соотношение
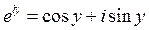 , (24.10)
, (24.10)
которое называется формулой Эйлера.
Для комплексных показателей остаются в силе основные правила действий с показателями; например, при умножении чисел показатели складываются, при делении – вычитаются, при возведении в степень – перемножаются.
Показательная функция имеет период, равный 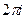 , то есть
, то есть 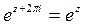 . В частности, при
. В частности, при 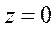 получается соотношение
получается соотношение 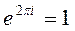 .
.
Тригонометрическую форму комплексного числа 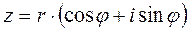 можно заменить показательной формой:
можно заменить показательной формой: 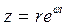 .
.
Умножение, деление, возведение в целую положительную степень и извлечение корня целой положительной степени для комплексных чисел, заданных в показательной форме, выполняются по следующим формулам:
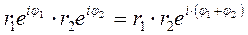 ; (24.11)
; (24.11)
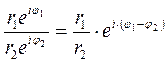 ; (24.12)
; (24.12)
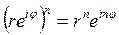 ; (24.13)
; (24.13)
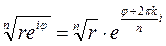 , где
, где 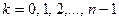 . (24.14)
. (24.14)
Примеры
Задание 1: Выполните действия:
1) 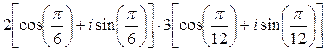 ;
;
2) 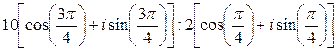 .
.
Решение: 1) По формуле умножения комплексных чисел заданных в тригонометрической форме получим
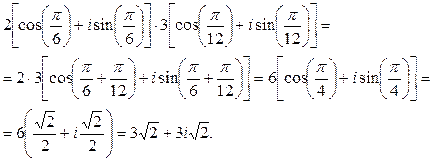
2) По формуле деления комплексных чисел заданных в тригонометрической форме получим
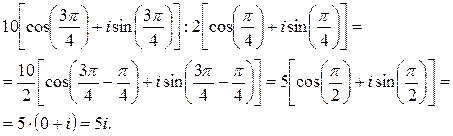
Задание 2: Возвести в степень 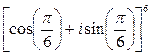 .
.
Решение: По формуле Муавра получим
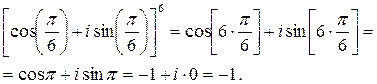
Задание 3: Найти: 1) 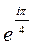 ; 2)
; 2) 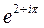 .
.
Решение: 1) По формуле Эйлера получим
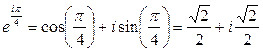 ;
;
2) По формуле (1) получим 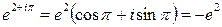 .
.
Задание 4: Найти: 1) 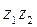 ; 2)
; 2) 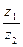 ; 3)
; 3) 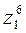 , если
, если 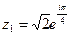 ;
; 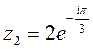 .
.
Решение: 1) По формуле умножения комплексных чисел, заданных в показательной форме получим
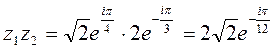 .
.
2) По формуле деления комплексных чисел, заданных в показательной форме получим
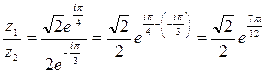 .
.
3) По формуле возведения комплексных чисел, заданных в показательной форме, в степень получим
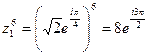 .
.
Задания для практической работы
1. Найдите произведение (ответ записать в тригонометрической форме):
1) 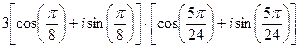 ;
;
2) 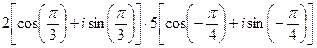 ;
;
3) 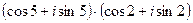 ;
;
4) 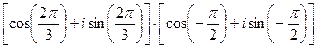 ;
;
5) 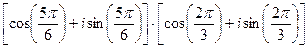 .
.
2. Выполните деление в тригонометрической форме:
1) 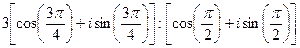 ;
;
2) 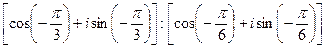 ;
;
3) 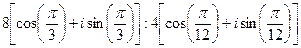 ;
;
4) 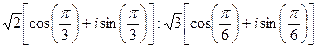 .
.
3. Найдите:
1) 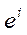 ; 2)
; 2) 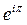 ; 3)
; 3) 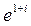 ; 4)
; 4) 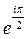 ;
;
5) 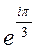 ; 6)
; 6) 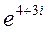 ; 7)
; 7) 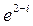 ; 8)
; 8) 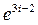 .
.
4. Дано 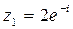 ;
; 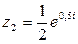 .
.
Найдите: 1) 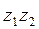 ; 2)
; 2) 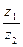 ; 3)
; 3) 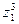 .
.
5. Решите уравнения:
1) 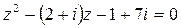 ;
;
2) 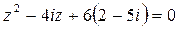 ;
;
3) 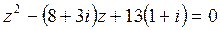 .
.
Контрольные вопросы:
1. Дайте определение комплексного числа.
2. Какие числа называются комплексно – сопряженными?
3. Какие комплексные числа называются равными?
4. Дайте определение тригонометрической формы комплексного числа.
5. Как умножаются и делятся комплексные числа, заданные в тригонометрической форме?
6. Как возводится в степень комплексное число, заданное в тригонометрической форме?
7. По какой формуле извлекается корень 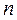 -ой степени из комплексного числа, заданного в тригонометрической форме?
-ой степени из комплексного числа, заданного в тригонометрической форме?
8. Как записывается комплексное число в показательной форме?
9. Что называется тождеством Эйлера?
10. Какие действия выполняются над комплексными числами, заданными в показательной форме? Запишите формулы.
Рекомендуемая литература: 1.2[с. 229-239].
Практическая работа №25
