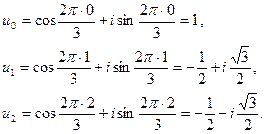Действия над комплексными числами, заданными в тригонометрической форме

Умножение.

При перемножении чисел z₁ и z₂, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:

z = z₁z₂ = r₁r₂×( cos( j₁ + j₂ ) + isin( j₁ + j₂ )).

(Формула справедлива для любого конечного числа сомножителей.)

z₁…z_n = r₁…r_n ( cos(j₁ +…+j_n) + isin(j₁ +…+j_n )).

Если z₁ = z₂ =…= z_n = z = r(cosj + isinj), то последняя принимает вид

zⁿ = rⁿ×(cosnj + isin nj )

и называется формулой Муавра. Она показывает, что для возведения комплексного числа в натуральную степень нужно возвести в эту степень его модуль, а аргумент умножить на показатель степени.

Примеры.

1) Выполнить умножение: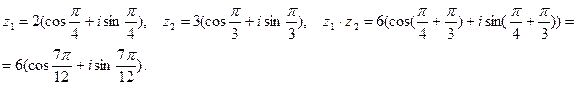

2) Вычислить: .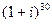

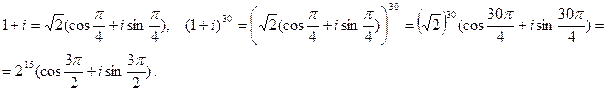
2. Деление.

Если z₁ = r₁×( cosj₁ + isinj₁) и z₂ = r₂×( cosj₂ + isinj₂ ), то

,

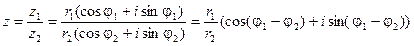т.е. модуль частного двух комплексных чисел z₁ и z₂ равен частному модулей, а аргумент частного – разности аргументов.

Пример.

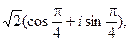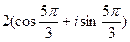z₁ = z₂ = . Найти частное.

.

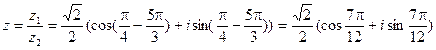Формула Муавра ( 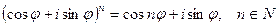) находит много применений. Так, например, если n = 3, то, возведя левую часть по формуле сокращенного умножения в куб, получим равенство

.

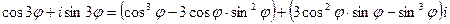Из равенства комплексных чисел и основного тригонометрического тождества получаем

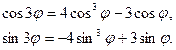
С помощью формулы Муавра можно находить суммы тригонометрических функций.

Например, найдем сумму 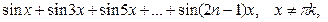k Î Z.

Рассмотрим сумму .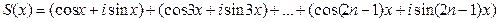

Из формулы Муавра имеем: .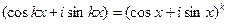

Таким образом, сумма S(x) примет вид:

.

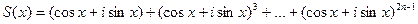Эта сумма есть геометрическая прогрессия из n слагаемых с первым членом 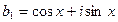и знаменателем прогрессии 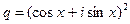. По формуле 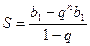для суммы n членов геометрической прогрессии, имеем

.

.

.

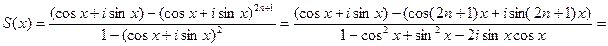
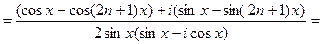
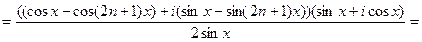
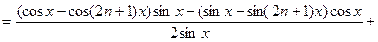
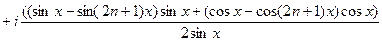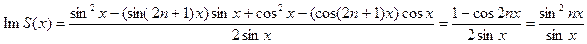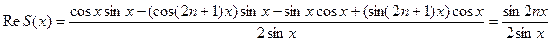В исходном выражении для S(x) было:

,

.

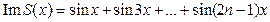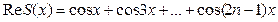Сравнивая мнимые и действительные части, получаем следующие формулы:

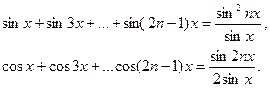
Извлечение корня из комплексного числа

Корнем n-ой степени, n Î N, n ³ 2, из числа z называется любое комплексное число u, для которого n-ая степень равна z:

.

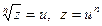В поле комплексных чисел справедлива следующая теорема.

Для любого z ≠ 0 извлечение корня n-ой степени, n ³ 2, из числа z всегда возможно и имеет ровно n различных значений.

Пусть z = r(cosj + isinj). Искомый корень n-ой степени обозначим

u = r(cosq + isinq).

По определению корня имеем uⁿ = z. Откуда следует, что

rⁿ (cosnq + isinnq) = r(cosj + isinj).

Из равенства комплексных чисел получаем:

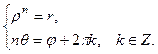
Так как .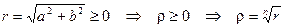

Таким образом, модуль комплексного числа u определяется как арифметический корень из действительного положительного числа r, а аргумент находят по формуле

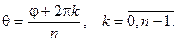
Общая формула Муавра

,

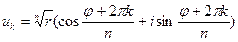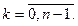
Пример.

Вычислить u = .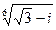

Представим число z = 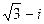в тригонометрической форме:

,

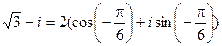Поэтому согласно общей формуле Муавра

,

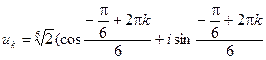где k = 0, 1, 2, 3, 4, 5.

Таким образом, значения корней:

,

,

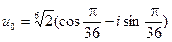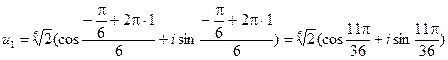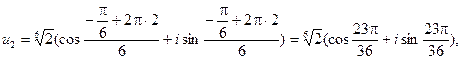
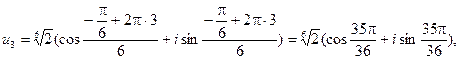
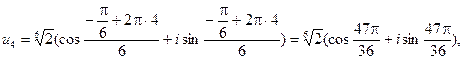
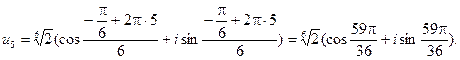
Геометрически корни можно интерпретировать как числа, изображающие в комплексной плоскости вершины правильного n угольника (в рассмотренном примере – шестиугольника ), вписанного в окружность радиусом 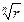(в рассмотренном примере – радиусом 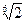), с центром в начале координат.

Примеры.

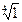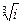Найти: 1) , 2) , 3) .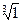

Решение.

1) ,

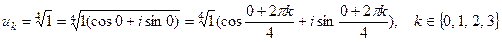u₀ = cos0 + isin0 = 1,

,

,

.

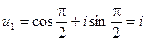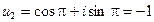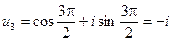2)

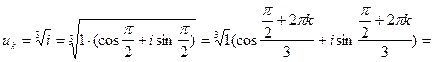
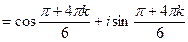, k = 0, 1, 2.

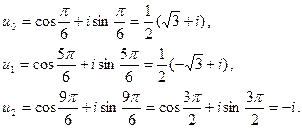
3) 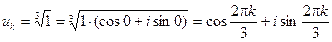, k = 0, 1, 2.