Тема: Вычисление односторонних пределов, классификация точек разрыва
Цель: Формирование навыков вычисления односторонних пределов, классификации точек разрыва
Время выполнения: 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Функция 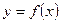 называется непрерывной в точке
называется непрерывной в точке 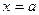 , если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть
, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть 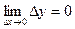 . (9.1)
. (9.1)
Функция 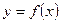 называется непрерывной в точке
называется непрерывной в точке 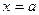 , если существует конечный предел функции в этой точке, который равен значению функции в точке
, если существует конечный предел функции в этой точке, который равен значению функции в точке 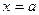 , то есть
, то есть 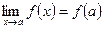 . (9.2)
. (9.2)
Примером непрерывной функции может служить любая элементарная функция, которая непрерывна в каждой точке своей области определения.
Точка 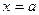 называется точкой разрыва функции
называется точкой разрыва функции 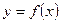 , если эта функции определена в некоторой окрестности точки
, если эта функции определена в некоторой окрестности точки 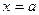 , но в самой точке
, но в самой точке 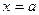 не удовлетворяет условию непрерывности.
не удовлетворяет условию непрерывности.
Точки разрыва функции делятся два типа. К точкам разрыва I рода относятся такие точки, в которых существуют конечные односторонние пределы: 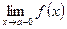 (левый предел) и
(левый предел) и 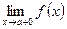 (правый предел). К точкам разрыва II рода относятся те точки, в которых хотя бы один из односторонних пределов не существует или бесконечен.
(правый предел). К точкам разрыва II рода относятся те точки, в которых хотя бы один из односторонних пределов не существует или бесконечен.
Заметим, что точки разрыва I рода подразделяются в свою очередь на точки устранимого разрыва (когда 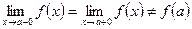 ) и на точки скачка функции (когда
) и на точки скачка функции (когда 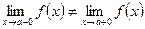 ); в последнем случае разность
); в последнем случае разность 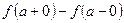 называется скачком функции
называется скачком функции 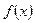 в точке
в точке 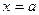 .
.
Пример
Задание 1: Вычислите односторонние пределы: 1) 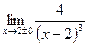 ;
;
2) 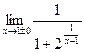 .
.
Решение: 1) Пусть 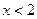 . Тогда при
. Тогда при 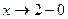 функция
функция 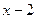 , а, следовательно, и
, а, следовательно, и 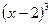 есть отрицательная бесконечно малая, поэтому функция
есть отрицательная бесконечно малая, поэтому функция 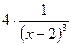 - отрицательная бесконечно большая, то есть
- отрицательная бесконечно большая, то есть 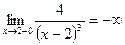 .
.
При 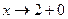 функция
функция 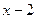 , а, следовательно, и
, а, следовательно, и 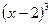 - положительная бесконечно большая функция, то есть
- положительная бесконечно большая функция, то есть 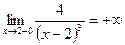 .
.
2) Пусть 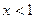 . Тогда при
. Тогда при 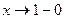 имеем:
имеем: 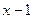 - отрицательная бесконечно малая функция; следовательно,
- отрицательная бесконечно малая функция; следовательно, 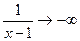 и
и 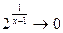 . Отсюда
. Отсюда 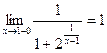 .
.
Если 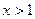 , то при
, то при 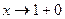 получим:
получим: 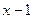 - положительная бесконечно малая функция; следовательно,
- положительная бесконечно малая функция; следовательно, 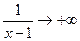 и
и 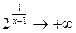 , тогда
, тогда 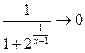 . Имеем,
. Имеем, 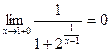 .
.
Задание 2: Даны функции: 1) 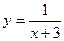 ; 2)
; 2) 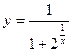 . Найти точки разрыва и исследовать их характер.
. Найти точки разрыва и исследовать их характер.
Решение: 1) Функция 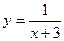 определена при всех значениях
определена при всех значениях 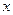 , кроме
, кроме 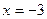 . Так как эта функция является элементарной, то она непрерывна в каждой точке своей области определения, состоящей из двух промежутков
. Так как эта функция является элементарной, то она непрерывна в каждой точке своей области определения, состоящей из двух промежутков 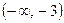 и
и 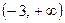 .
.
Следовательно, единственной точкой разрыва является точка 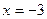 (функция определена в окрестности этой точки, в самой же точке нарушается условие непрерывности – функция в ней неопределена). Для исследования характера разрыва найдем левый и правый пределы этой функции при стремлении аргумента к точке разрыва
(функция определена в окрестности этой точки, в самой же точке нарушается условие непрерывности – функция в ней неопределена). Для исследования характера разрыва найдем левый и правый пределы этой функции при стремлении аргумента к точке разрыва 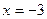 :
:
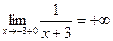 ,
, 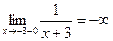 .
.
Следовательно, при 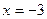 функция
функция 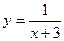 имеет бесконечный разрыв;
имеет бесконечный разрыв; 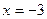 есть точка II рода.
есть точка II рода.
2) Рассуждая аналогично, получим, что точкой разрыва заданной функции является 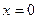 . Найдем односторонние пределы этой функции в точке
. Найдем односторонние пределы этой функции в точке 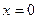 :
: 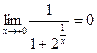 ,
, 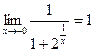 .
.
Таким образом, левый и правый пределы исследуемой функции при 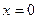 конечны, но не равны между собой. Поэтому
конечны, но не равны между собой. Поэтому 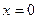 точка I рода, причем точка скачка функции.
точка I рода, причем точка скачка функции.
Задания для практической работы
1. Вычислите односторонние пределы:
1) 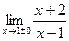 ; 2)
; 2) 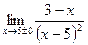 ; 3)
; 3) 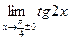 ;
;
4) 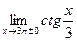 ; 5)
; 5) 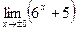 ; 6)
; 6) 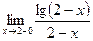 .
.
2. Для данных функций найдите точки разрыва и исследуйте их характер:
1) 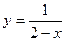 ; 2)
; 2) 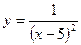 ; 3)
; 3) 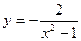 ;
;
4) 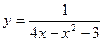 ; 5)
; 5) 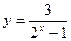 ; 6)
; 6) 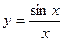 .
.
3. Исследуйте на непрерывность функции:
1) 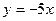 ; 2)
; 2) 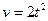 ; 3)
; 3) 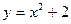 ;
;
4) 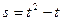 ; 5)
; 5) 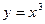 ; 6)
; 6) 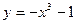 .
.
Контрольные вопросы:
1. Дайте определение непрерывной функции.
2. Что называется точкой разрыва?
3. На какие два типа делятся точки разрыва? Дайте определение.
4. Какие пределы называются односторонними?
5. Какая точка называется точкой устранимого разрыва?
6. Какая точка называется точкой скачка? Что называется скачком?
Рекомендуемая литература: 1.2[с. 71-87], 2.1[с.142-149].
Практическая работа №10
