III. Задачи, приводящие к уравнениям гиперболического, параболического и эллиптического типов. Начальные и краевые условия.

Волновое уравнение(уравнение гиперболического типа)

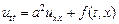. (3.1)

Это уравнение описывает движение струны (т.е. тонкой однородной нерастяжимой нити), свободно изгибающейся в вертикальной плоскости. Неизвестная функция 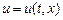зависит от времени 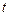и координаты струны 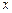. При каждом фиксированном 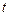функция 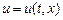представляет собой профиль струны, который можно представить как некоторую непрерывную гладкую кривую в плоскости 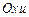. Коэффициент 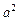определяется характеристиками струны и для данной струны является постоянной величиной. Функция 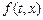– заданная функция, описывающая внешние воздействия на струну. Если 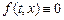, то уравнение (3.1) называют уравнением свободных колебаний; если 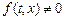, то говорят о вынужденных колебаниях струны.

Переменная 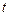(время) предполагается неотрицательной, т.е. 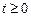, что вполне объяснимо, поскольку наблюдения над струной можно считать начатыми в некоторый момент времени, который мы вправе, не нарушая общности, назвать нулем.

Для области изменения координаты 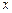существует гораздо больше возможностей.

Во-первых, можно предполагать, что 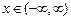; это предположение соответствует случаю бесконечной струны. Не следует считать, что такая постановка задачи не физична, т.е. не имеет никакого отношения к реальности. Представим себе, что нас интересует поведение очень длинной струны, причем на небольшом серединном участке. При таких предположениях малосущественно, как ведет себя струна на концах – эта информация просто не будет востребована. Для такого случая модель бесконечной струны оказывается вполне адекватной.

Во-вторых, можно считать, что 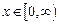; получаем случай полубесконечной струны. И снова эта модель окажется удобной для очень длинной струны, но рассматриваемой вблизи одного из ее концов.

В-третьих, можно считать, что 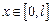, и рассмотреть струну конечной длины. В этом случае поведением струны на концах пренебречь нельзя: из самых общих предположений ясно, что ситуация жесткого закрепления на концах существенно отличается, скажем, от ситуации свободно движущегося конца струны.

Заметим, что три приведенных выше варианта выбора области определения для переменной 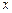приводят к различным методам решения соответствующих задач.

Следующий вопрос, без ответа на который нельзя обойтись – наличие начальных условий на функцию 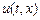. Такие условия необходимы: ведь уравнение (3.1) – дифференциальное, значит, его решение будет содержать произвольные параметры, для вычисления которых нужны дополнительные условия. Добавим к уравнению (3.1) два начальных условия:

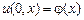– начальный профиль струны, (3.2)

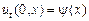– начальная скорость струны. (3.3)

Если дополнить уравнение (3.1) условиями (3.2) и (3.3), то мы получим для волнового уравнения аналог задачи Коши. В случае бесконечной струны для однозначной разрешимости задачи Коши достаточно задать начальный профиль и начальное распределение скоростей. Для полубесконечной или конечной струны потребуются еще условия на границах.

Решение задачи о колебаниях плоской однородной мембраны приводит к двумерному волновому уравнению:

,

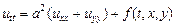а задача о движении газа или жидкости в пространстве – к трехмерному уравнению:

.

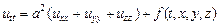Задание начальных условий при этом существенно не меняется, а краевые условия усложняются: вместо одной или двух точек, ограничивающих струну, придется иметь дело с границей плоской области или поверхностью трехмерного тела.

Уравнение теплопроводности (уравнение параболического типа)

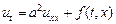. (3.4)

Это уравнение описывает закон распределения температуры в тонком однородном изотропном стержне с теплоизолированной боковой поверхностью (теплообмен с окружающей средой происходит только через концы стержня).

Неизвестная функция 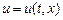зависит от времени 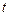и координаты стержня 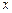. При каждом фиксированном функция 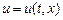есть температура поперечного сечения стержня, определяемого координатой 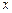(так как стержень тонкий и однородный, то можно считать, что все точки поперечного сечения имеют одинаковую температуру). Положительный коэффициент 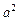называют коэффициентом температуропроводности; он зависит от материала, из которого изготовлен стержень и для данного стержня является постоянной величиной. Если функция 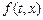ненулевая, то в стержне есть внутренние источники тепла с плотностью распределения .

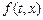Так же как и для струны считаем, что 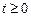, а для 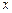есть три существенно различных области изменения:

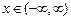– бесконечный стержень; моделирует ситуацию очень длинного стержня, если нас интересует распределение тепла на небольшом участке вдали от концов;

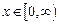– полубесконечный стержень – исследуется распределение тепла в длинном стержне вблизи одного из концов;

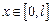– стержень конечной длины.

Так как уравнение (3.4) по переменной 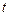является уравнением первого порядка, то для него нужно только одно начальное условие:

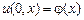– начальная температура стержня. (3.5)

Для бесконечного стержня задача (3.4)–(3.5) однозначно разрешима. Для конечного и полубесконечного стержня нужна информация о тепловом режиме на границах.

Уравнение стационарных процессов(уравнение эллиптического типа)

Если процессы, описываемые волновым уравнением или уравнением теплопроводности, не зависят от времени (стационарный процесс), то мы приходим к уравнениям эллиптического типа. Они описывают также течение идеальной (невязкой и несжимаемой) жидкости, потенциал электрического поля в однородной проводящей среде.

Например, стационарное распределение тепла в плоской однородной пластинке D описывается уравнением

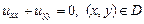(3.6)

с заданными условиями на границе пластинки ∂D

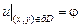. (3.7)

В физической постановке задача, моделью которой являются соотношения (3.6) – (3.7), может быть сформулирована следующим образом: найти температуру 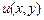всех точек пластинки D, остающуюся постоянной (т.е. не меняющуюся со временем), если на границе пластинки поддерживается заданная температура j. Эта задача носит название задачи Дирихле.

Если условие (3.7) заменить условием 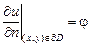(здесь 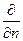– производная по внешней нормали к границе ∂D), то эту задачу называют задачей Неймана.