Задача 3. Линейные дифференциальные уравнения первого порядка.

Линейным дифференциальным уравнением первого порядка называется уравнение линейное относительно неизвестной функции и ее производной. Оно имеет вид

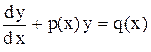(1)

где 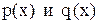- заданные функции от 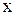, непрерывные в той области, в которой требуется проинтегрировать уравнение (1).

Если 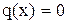, то уравнение (1) называется линейным однородным. Оно является уравнением с разделяющимися переменным и имеет общее решение

.

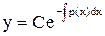Общее решение неоднородного уравнения можно найти следующими способами:

1) методом вариации произвольной постоянной, который состоит в том, что

решение уравнения (1) находится в ви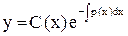де

, где 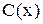- новая неизвестная функция.

2) уравнение (1) может быть проинтегрирован с помощью подстановки 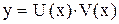, где 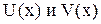- неизвестные функции от .

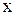3) решение уравнения (1) можно найти еще и по формуле

.

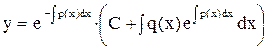Замечание. Может оказаться, что дифференциальное уравнение линейно относительно 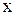как функции от 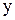. Нормальный вид (коэффициент при 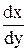равен 1) такого уравнения

( )

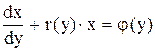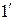Пример 4.

Решить уравнение .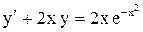

Решение. Вид уравнения нормальный

.

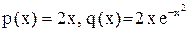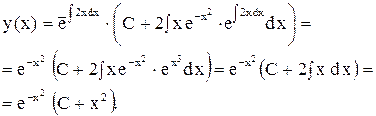
Ответ: .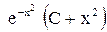

Упражнения. Решить уравнения

1. 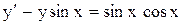. Ответ: .

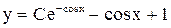2. .

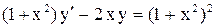Приводим к виду 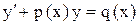, 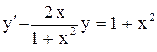и решаем по формуле, которая была выведена на лекциях ( повторить, потому, что вывод спрашивают !) 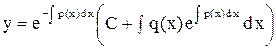. Ответ: .

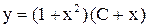3. 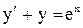. Ответ: .

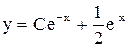4. 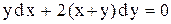. Ответ: .

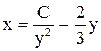Уравнение линейное относительно функции 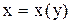. Приводим его к виду

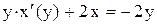или .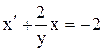

Решить линейные дифференциальные уравнения первого порядка:

1.	.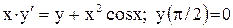
2.	.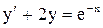
3.	; .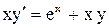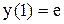
4.	.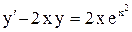
5.	.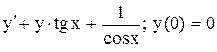
6.	.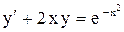
7.	.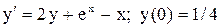
8.	.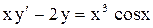
9.	.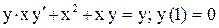
10.	.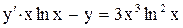
11.	.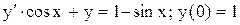
12.	.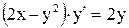
13.	.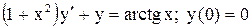
14.	.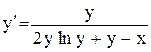
15.	.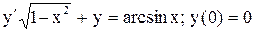
16.	.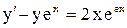
17.	.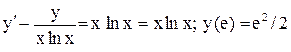
18.	.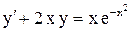
19.	.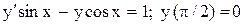
20.	.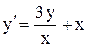
21.	.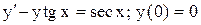
22.	.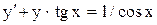
23.	.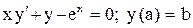
24.	.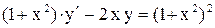
25.	.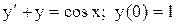
26.	.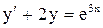
27.	.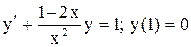
28.	.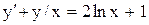
29.	.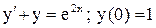
30.	.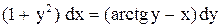

Задача 4. Уравнение Бернулли.

Уравнение Бернулли имеет вид

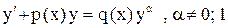(1)

(при 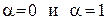это уравнение является линейным).

Уравнение (1) умножим на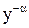

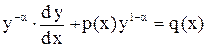(2)

Обозначим .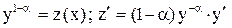

Уравнение (2) умножим на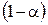

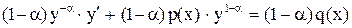или

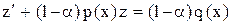(3)

(3) – линейное уравнение относительно переменной .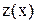

Таким образом, уравнение Бернулли можно привести к линейному уравнению.

Замечание. Уравнение Бернулли может быть проинтегрировано также методом вариации постоянной, как линейное уравнение и с помощью подстановки .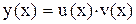

Пример 5.

Решить уравнение Бернулли .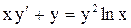

Приведем уравнение к виду

.

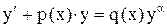
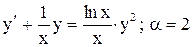Обе части уравнения умножим на 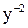и сделаем замену 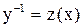, причем, 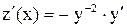, получим 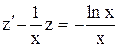- это линейное уравнение относительно .

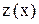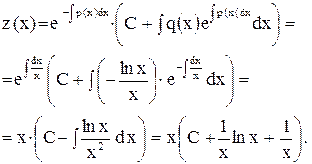
Получили .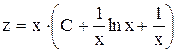

Поэтому .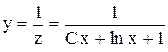

Ответ: .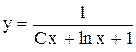

Упражнения. Решить уравнения

1. 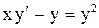. Ответ: .

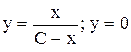2. 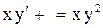. Ответ: .

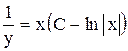3. 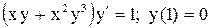. Ответ: .

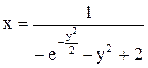Уравнение следует переписать в виде

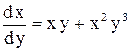или 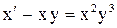- это уравнение Бернулли относительно функции .

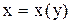4. 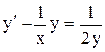. Ответ: .

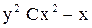Обе части уравнения следует умножить на 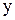и сделать замену .

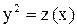Решить уравнения Бернулли:

1.	.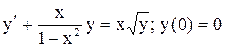
2.	.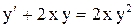
3.	.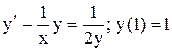
4.	.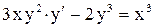
5.	.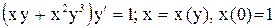
6.	.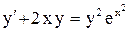
7.	.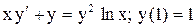
8.	.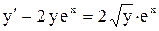
9.	.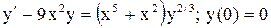
10.	.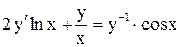
11.	.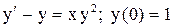
12.	.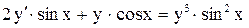
13.	.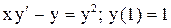
14.	.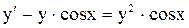
15.	.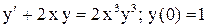
16.	.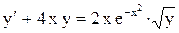
17.	.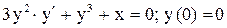
18.	.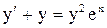
19.	.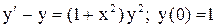
20.	.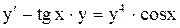
21.	.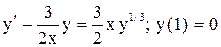
22.	.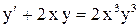
23.	.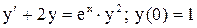
24.	.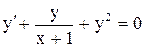
25.	.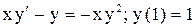
26.	.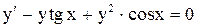
27.	.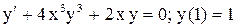
28.	.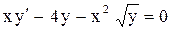
29.	.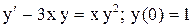
30.	.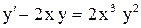

Задача 5. Уравнения в полных дифференциалах.

Дифференциальное уравнение вида

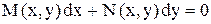(1)

называется уравнением в полных дифференциалах, если его левая часть представляет полный дифференциал некоторой функции 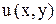, т.е.

.

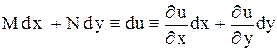Для того, чтобы уравнение (1) являлось уравнением в полных дифференциалах, необходимо и достаточно, чтобы в некоторой области 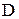изменения переменных 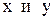выполнялось условие

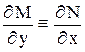(2)

В этом случае общий интеграл имеет вид 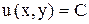или

.

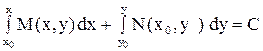Пример 6.

Решить уравнение .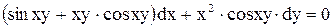

Решение. Проверим является ли данное уравнение уравнением в полных дифференциалах

.

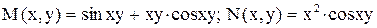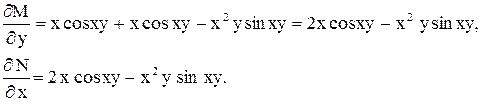
Получили, что 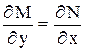, условие (2) выполнено, значит данное уравнение в полных дифференциалах.

Найдем функцию 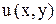. Для этого имеем систему:

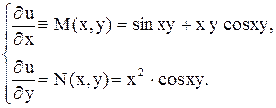
Из первого уравнения, интегрированием по 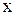при постоянном 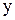, определяем :

,

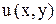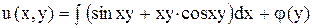где 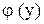- произвольная функция (вместо постоянной интегрирования С берем функцию )

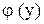Частная производная 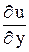, найденной функции 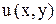должна равняться в силу второго уравнения системы, 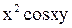, что дает

,

.

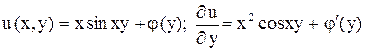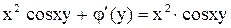Отсюда ,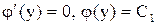

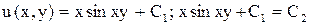- общий интеграл.

Ответ: 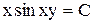, где .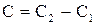

Упражнения. Решить уравнения

1. 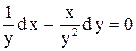. Ответ: .

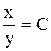2. 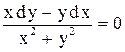. Ответ: .

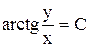3. 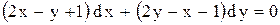. Ответ: .

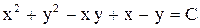4. 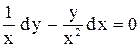. Ответ: .

,

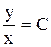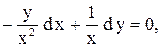
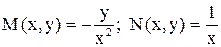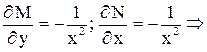уравнение в полных дифференциалах.

Проинтегрировать уравнения в полных дифференциалах:

1.	.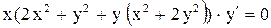
2.	.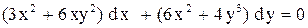
3.	.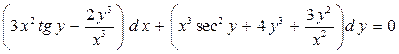
4.	.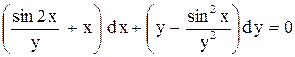
5.	.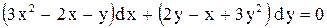
6.	.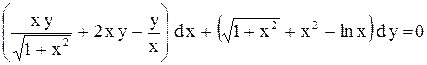
7.	.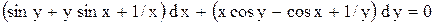
8.	.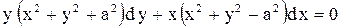
9.	.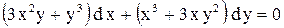
10.	.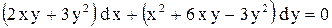
11.	.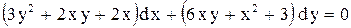
12.	.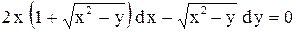
13.	.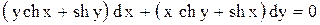
14.	.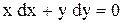
15.	.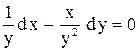
16.	.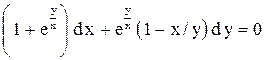
17.	.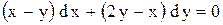
18.	.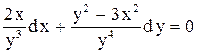
19.	.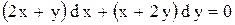
20.	.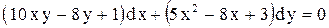
21.	.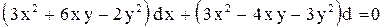
22.	.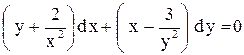
23.	.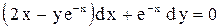
24.	.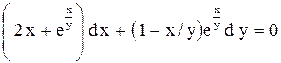
25.	.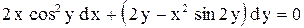
26.	.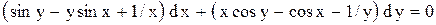
27.	.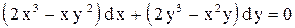
28.	.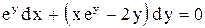
29.	.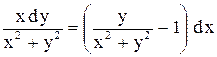
30.	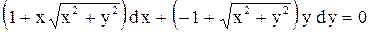.