ЗАНЯТИЕ 3. Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли.
| Ауд. | Л-3 | гл.10: № 67, 68, 74, 78, 83, 86, 92, 95,179, 193. |
☺ ☻ ☺
Пример 1–67: Решить дифференциальное уравнение: y′+2xy=x 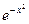 . (1)
. (1)
Решение:
1). Приводим уравнение к «стандартной форме»: y′+P(x)∙y=Q(x).
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде: функции y=u∙v.
a1. Вычислим интеграл: – 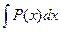 и запишем: u=
и запишем: u= 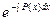 .
.
a2. Вычислим функцию v: v = 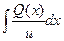 +С.
+С.
a3. Запишем общее решение уравнения: y=u∙v= 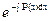 ∙
∙ 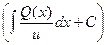 .
.
3). В нашем случае: уравнение линейное, имеет «стандартную форму»: y′+P(x)∙y=Q(x)!
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1. Вычислим интеграл: – 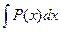 =–2
=–2 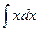 =– x2 → u=
=– x2 → u= 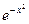 .
.
a2. Вычислим функцию v: v = 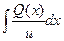 +С=
+С= 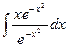 +С =
+С = 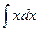 =
= 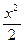 +С;
+С;
a3. Запишем общее решение уравнения: y=u∙v= 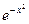 ∙
∙ 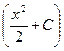 .
.
Ответ: y=u∙v= 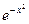 ∙
∙ 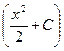 – общее решение.
– общее решение.
Пример 2–68: Решить дифференциальное уравнение: y′ =3 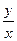 +x.
+x.
Решение:
1). Приводим уравнение к «стандартной форме»: y′–3 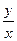 ∙y=x.
∙y=x.
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1. Вычислим интеграл: – 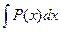 =3
=3 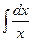 =3ln|x| → u=
=3ln|x| → u= 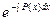 =x3.
=x3.
Замечание: в последней записи выражения для u знак модуля опущен, так как от функции u(x) требуется только обеспечить выполнение равенства: u′+ P(x)∙u=0 (см. вывод формулы для решения y = u(x)∙v(x)!).
a2. Вычислим функцию v: v = 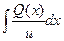 +С=
+С= 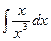 +С =–
+С =– 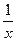 +С.
+С.
a3. Запишем общее решение уравнения: y=u∙v=x3∙ 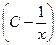 =Сx3– x2.
=Сx3– x2.
Ответ: y=u∙v= Сx3– x2– общее решение.
Пример 3–74: Решить дифференциальное уравнение: y′ = 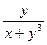 .
.
Решение:
1). Приводим уравнение к «стандартной форме»: x′– 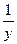 ∙x= y2. Переход от записи решения в виде y=y(x) к записи x=x(y) подсказан исходным выражением вполне выразительно!
∙x= y2. Переход от записи решения в виде y=y(x) к записи x=x(y) подсказан исходным выражением вполне выразительно!
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: x=u(y)∙v(y).
a1. Вычислим интеграл: – 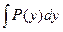 =
= 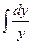 =ln|y| → u=
=ln|y| → u= 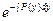 =y.
=y.
Замечание: в последней записи выражения для u знак модуля опущен (см. Пример 2-68).
a2. Вычислим функцию v: v = 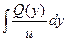 +С=
+С= 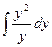 +С =
+С = 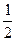 y2+С.
y2+С.
a3. Запишем общее решение уравнения: x=u∙v= y ∙ 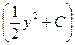 =Сy+
=Сy+ 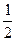 y3.
y3.
Ответ: x=u∙v= Сy+ 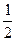 y3 – общее решение. Из исходного уравнения также: y=0 – решение.
y3 – общее решение. Из исходного уравнения также: y=0 – решение.
Пример 4–78: Решить дифференциальное уравнение: xy′+x2+xy=y.
Решение:
1). Приводим уравнение к «стандартной форме»: y′+ 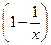 ∙y = –x. Переход от записи решения в виде y=y(x) к записи x=x(y) подсказан исходным выражением вполне выразительно!
∙y = –x. Переход от записи решения в виде y=y(x) к записи x=x(y) подсказан исходным выражением вполне выразительно!
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: y=u(x)∙v(x).
a1. Вычислим интеграл: – 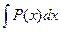 =
= 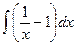 =ln|x|– x → u=
=ln|x|– x → u= 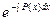 =xe–x.
=xe–x.
Замечание: в последней записи выражения для u знак модуля опущен (см. Пример 2-68).
a2. Вычислим функцию v: v = 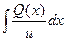 +С=
+С=  +С =–ex+С.
+С =–ex+С.
a3. Запишем общее решение уравнения: y=u∙v= xe–x∙ 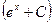 =x∙(Сe–x–1).
=x∙(Сe–x–1).
Ответ: y=u∙v= x∙(Сe–x–1) – общее решение.
Пример 5–83: Решить дифференциальное уравнение: y′ +y∙tgx = 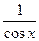 , y(0)=0.
, y(0)=0.
Решение:
1). Уравнение записано в «стандартной форме».
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1. Вычислим интеграл: – 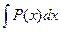 =–
=– 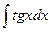 =ln|cosx| → u=
=ln|cosx| → u= 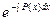 = cosx.
= cosx.
Замечание: в последней записи выражения для u знак модуля опущен (см. Пример 2-68).
a2. Вычислим функцию v: v = 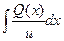 +С=
+С= 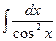 +С =tgx+С.
+С =tgx+С.
a3. Запишем общее решение уравнения: y=u∙v= cosx ∙ 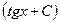 = sinx+Сcosx.
= sinx+Сcosx.
a4. Найдем частное решение уравнения: 0= sin0+Сcos0 → С=0; y= sinx– частное решение уравнения для начальных условий: y(0)=0.
Ответ: y= sinx+Сcosx – общее решение; y= sinx – частное решение.
Пример 6–86: Решить дифференциальное уравнение: y′+4xy=2x∙ 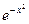 ∙
∙ 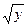 . (1)
. (1)
Решение:
1). Имеем уравнение (1) Бернулли в «стандартной форме».
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Примем: z = y–n+1;
a1. Запишем преобразованное уравнение Бернулли: z′+(–n+1)P(x)∙ z=(–n+1)Q(x), или (для удобства!): z′+P1(x)∙z=Q1 (x);
a2. Решение уравнения ищем в виде функции: z=u(x)∙v(x).
a3. Вычислим интеграл: – 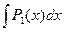 → u=
→ u= 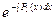 .
.
a4. Вычислим функцию v: v = 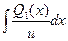 +С.
+С.
a5. Запишем общее решение уравнения: z=u∙v= 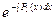 ∙
∙ 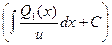 .
.
3). В нашем случае: уравнение Бернулли в «стандартной форме», для n= 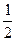 .
.
a0. Примем: z = y–n+1, где (–n+1)= 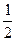 ; то есть: z=
; то есть: z= 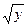 .
.
a1. Запишем преобразованное уравнение Бернулли: z′+ 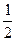 4x∙z=
4x∙z= 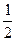 2x∙
2x∙ 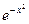 , или:
, или:
z′+2x∙z= x∙ 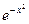 . (2)
. (2)
a2. Решение уравнения ищем в виде функции: z=u(x)∙v(x).
a3. Вычислим интеграл: – 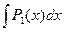 =–
=– 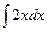 =–x2 → u=
=–x2 → u= 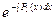 =
= 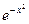 .
.
a4. Вычислим функцию v: v = 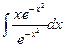 +С=
+С= 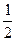 x2+С.
x2+С.
a5. Запишем общее решение уравнения для (2): z=u∙v= 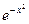 ∙
∙ 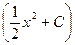 . (3)
. (3)
a6. Учитывая: z= 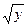 , запишем общее решение для (1):
, запишем общее решение для (1): 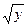 =
= 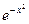 ∙
∙ 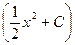 .
.
Ответ: 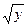 =
= 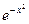 ∙
∙ 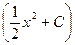 – общее решение.
– общее решение.
Пример 7–92: Решить дифференциальное уравнение: xy′+y=2x2∙ ylny ∙ y′. (1)
Решение:
1). Очевидно: (1) не является уравнением Бернулли для y, y′. Это подсказывает необходимость перехода к функции x=x(y): x′+ 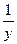 x=2lny∙x2. (2)
x=2lny∙x2. (2)
2). Получили уравнение (2) Бернулли в «стандартной форме», для n=2.
a0. Примем: z = x–n+1, где (–n+1)= –1; то есть: z= x–1.
a1. Запишем преобразованное уравнение Бернулли: z′– 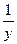 z= –2lny. (3)
z= –2lny. (3)
a2. Решение уравнения ищем в виде функции: z=u(y)∙v(y);
a3. Вычислим интеграл: – 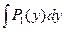 =
= 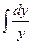 =lny → u=
=lny → u= 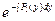 = y.
= y.
Замечание: в последней записи выражения для u знак модуля опущен, так как исходное выражение предполагает y >0.
a4. Вычислим функцию v: v = 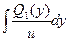 = –2
= –2 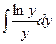 +С= – ln2y +С;
+С= – ln2y +С;
a5. Запишем общее решение уравнения для (3): z=u∙v= y∙ 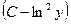 . (4)
. (4)
a6. Учитывая: z= x–1, запишем общее решение для (1): xy 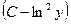 =1.
=1.
Ответ: xy 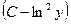 =1 – общее решение уравнения.
=1 – общее решение уравнения.
Пример 8–95: Решить дифференциальное уравнение: ydx+ 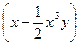 dy =0, y
dy =0, y 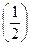 =1. (1)
=1. (1)
Решение:
1). Очевидно: (1) не является уравнением Бернулли для y, y′. Это подсказывает необходимость перехода к функции x=x(y): x′+ 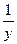 x=
x= 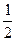 x3. (2)
x3. (2)
3). Получили уравнение (2) Бернулли в «стандартной форме», для n=3.
a0. Примем: z = x–n+1, где (–n+1)= –2; то есть: z= x–2.
a1. Запишем преобразованное уравнение Бернулли: z′–2 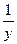 z= –1. (3)
z= –1. (3)
a2. Решение уравнения ищем в виде функци: z=u(y)∙v(y);
a3. Вычислим интеграл: – 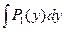 =2
=2 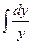 =2ln|y| → u=
=2ln|y| → u= 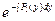 = y2.
= y2.
Замечание: в последней записи выражения для u знак модуля опущен (см. Пример 2-68). В то же время есть возможность записать: 2ln|y| = lny2.
a4. Вычислим функцию v: v = 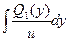 = –
= – 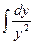 +С=
+С= 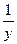 +С.
+С.
a5. Запишем общее решение уравнения для (3): z=u∙v=y2∙ 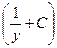 . (4)
. (4)
a6. Учитывая: z=x–2, запишем общее решение для (1): x2(y + Сy2)=1.
a7. Найдем частное решение для (1): так как 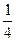 (1 + С12)=1 → С=3, то частное решение имеет вид: x2(y +3y2)=1.
(1 + С12)=1 → С=3, то частное решение имеет вид: x2(y +3y2)=1.
Ответ: x2(y + Сy2)=1 – общее решение уравнения; частное решение: x2(y +3y2)=1.
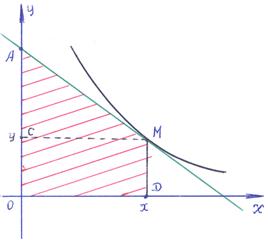 Пример 9–179: Найти уравнение кривой, проходящей через точку (1,0), если площадь трапеции, образованной касательной в этой точке, осями координат и ординатой точки касания, постоянна и равна
Пример 9–179: Найти уравнение кривой, проходящей через точку (1,0), если площадь трапеции, образованной касательной в этой точке, осями координат и ординатой точки касания, постоянна и равна 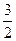 .
.
Решение:
В Примере 1–19 получено выражение: отрезка А=OА=(0,y–y′х), – отсекаемого касательной на оси ординат.
1). Так как площадь трапеции вычисляется по формуле: S= 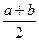 h, где a и b – стороны оснований, h – высота трапеции, условие задачи запишем так:
h, где a и b – стороны оснований, h – высота трапеции, условие задачи запишем так:
▪ (ОА+ND)∙ОD=2S=3 → (y–y′х+y)∙х =3; (1)
▪ (ОА+ND)∙ОD=2S=3 → (y–y′х+y)∙х =–3. (2)
Случай-1.
2). Запишем (1), в виде: y′– 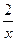 y=–
y=– 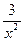 – «стандартная форма» линейного уравнения.
– «стандартная форма» линейного уравнения.
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1. Вычислим интеграл: – 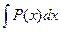 =2
=2 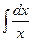 =2ln|x| → u=x2.
=2ln|x| → u=x2.
a2. Вычислим функцию v: v = 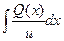 +С=–3
+С=–3 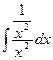 +С =x–3+С;
+С =x–3+С;
a3. Запишем общее решение уравнения: y=u∙v= x2∙( x–3+С)= 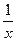 +Cx2.
+Cx2.
a4. Запишем частное решение уравнения: y= 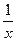 –x2, при С=–1.
–x2, при С=–1.
Случай-2.
3). Запишем (2), в виде: y′– 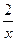 y=
y= 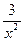 – «стандартная форма» линейного уравнения.
– «стандартная форма» линейного уравнения.
a0. Решение уравнения ищем в виде: функцию y=u∙v.
a1. Вычислим интеграл: – 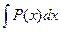 =2
=2 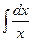 =2ln|x| → u=x2.
=2ln|x| → u=x2.
a2. Вычислим функцию v: v= 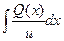 +С= 3
+С= 3 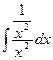 +С =–x–3+С;
+С =–x–3+С;
a3. Запишем общее решение уравнения: y=u∙v=x2∙(–x–3+С)=Cx2– 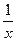 . Это решение «симметрично относительно оси ОХ» решению, полученному в Случае-1.
. Это решение «симметрично относительно оси ОХ» решению, полученному в Случае-1.
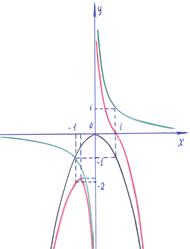
a4. Запишем частное решение уравнения: y= x2– 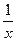 , при С=1.
, при С=1.
4). Построим эскиз графика функции y= 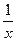 –x2, используя известные графики для гиперболы и параболы и применяя понятие «сумма функций» (см. рисунок).
–x2, используя известные графики для гиперболы и параболы и применяя понятие «сумма функций» (см. рисунок).
Ответ: для Случая-1: y= 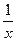 –x2 – частное решение ДУ; для Случая-2: y= x2–
–x2 – частное решение ДУ; для Случая-2: y= x2– 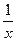 – частное решение ДУ.
– частное решение ДУ.
Замечание: Если не заметить присутствия двух различных вариантов решения рассмотренной задачи, то «зеркальное решение» будет потеряно. В задачах физики это дополнительно подсказывает важность понимания начальных условий исследуемого процесса: возможно исследователю потребуются дополнительные эксперименты для уточнения особенностей протекания процесса.
Пример 10–193: Лодка замедляет свое движение под действием сопротивления воды, которое пропорционально скорости лодки. Начальная скорость лодки 1.5 м/с, скорость её через 4 секунды равна 1м/с. Когда скорость уменьшится до 1 см/с? Какой путь пройдет лодка до остановки?
Решение:
Для решения задачи необходимо уточнить: система координат, используемая при решении задачи, связана с берегом реки и считается инерциальной. Это значит, что второй закон Ньютона в этой системе выполняется и можно записать дифференциальное уравнение:
m∙v′=– k∙v, (1)
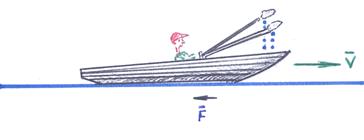 где m – масса лодки с гребцом; k – коэффициент торможения лодки из-за сопротивления воды. Движение лодки происходит по инерции (гребец «сушит весла»!).
где m – масса лодки с гребцом; k – коэффициент торможения лодки из-за сопротивления воды. Движение лодки происходит по инерции (гребец «сушит весла»!).
Обозначим: – 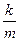 =μ и запишем уравнение в виде, удобном для интегрирования:
=μ и запишем уравнение в виде, удобном для интегрирования:
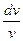 = μ∙dt. (2)
= μ∙dt. (2)
Интегрируя (2), получаем: v =v0∙eμt, где v0=1.5 м/с. В задаче не определены ни движущаяся масса, ни коэффициент трения лодки о воду. Но мы имеем дополнительные сведения (легко устанавливается экспериментально!), которые позволят полностью определить закон движения лодки.
Из условия: для t=4c имеем v = 1 [м/с] → 1=1.5∙ eμ4. Отсюда: (eμ)4= 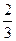 ≈ 0.67 и eμ ≈
≈ 0.67 и eμ ≈ 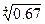 =λ.
=λ.
Итак, закон движения: v =v0∙λt. У нас v =1.5∙λt. После этого можем определить время, когда скорость лодки уменьшилась до 1 см/с: 0.01=1.5∙λt, откуда → t ≈ 50с.
Для ответа на второй вопрос необходимо проинтегрировать уравнение: dx=1.5∙λtdt. Примем, что начальное положение лодки: x0=0. Тогда x=1.5∙ 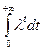 =1.5∙lnλ(0–λt) ≈ 15м.
=1.5∙lnλ(0–λt) ≈ 15м.
Замечание: при вычислении несобственного интеграла учтено, что для верхнего предела значение этого интеграла равно нулю!
Ответ: Время: t ≈ 50с. До полной остановки лодка переместится на расстояние x ≈ 15м (это будет проистекать бесконечно долго!).
* * * * * * * * * *
Домашнее задание
| Дома | Л-2 | гл.10: № 70, 71, 72, 75, 85, 87, 89, 94, 180, 198. |
Пример 1–70: Решить дифференциальное уравнение: (1+ x2)y′= 2xy+(1+ x2)2. (1)
Решение:
1). Так как заданное уравнение не «стандартной формы», приводим его к стандартной форме: y′+P(x)∙y=Q(x), то есть: y′– 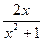 y= x2+1. (2)
y= x2+1. (2)
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1. Вычислим интеграл: – 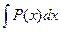 и запишем: u=
и запишем: u= 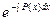 .
.
a2. Вычислим функцию v: v = 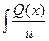 +С.
+С.
a3. Запишем общее решение уравнения: y=u∙v= 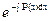 ∙
∙ 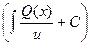 .
.
3). В нашем случае: уравнение линейное, имеет «стандартную форму»: y′+P(x)∙y=Q(x)!
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1. Вычислим интеграл: – 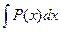 =–
=– 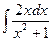 =–ln(x2+1) → u=
=–ln(x2+1) → u= 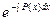 = x2+1.
= x2+1.
a2. Вычислим функцию v: v = 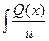 +С=
+С= 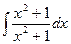 +С = x +С.
+С = x +С.
a3. Запишем общее решение уравнения: y=u∙v=(x2+1)∙(x +С).
Ответ: y=u∙v=(x2+1)∙(x +С) – общее решение.
Пример 2–71: Решить дифференциальное уравнение: y′ +2y =e3x.
Решение:
1). Уравнение записано в «стандартной форме».
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1. Вычислим интеграл: – 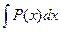 =–
=– 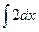 =–2x → u=
=–2x → u= 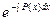 = e–2x.
= e–2x.
a2. Вычислим функцию v: v = 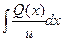 +С=
+С= 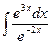 +С =
+С = 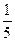 e5x +С.
e5x +С.
a3. Запишем общее решение уравнения: y=u∙v= e–2x ∙ 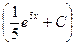 =
= 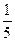 e3x +Сe–2x.
e3x +Сe–2x.
Ответ: y= 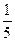 e3x +Сe–2x – общее решение.
e3x +Сe–2x – общее решение.
Пример 3–72: Решить дифференциальное уравнение: y′ + 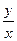 =2lnx +1.
=2lnx +1.
Решение:
1). Приведём уравнение к «стандартной форме»: y′ + 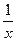 y =2lnx +1.
y =2lnx +1.
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1. Вычислим интеграл: – 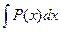 =–
=– 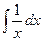 =– lnx → u=
=– lnx → u= 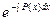 =
= 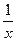 .
.
a2. Вычислим функцию v: v= 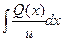 +С=
+С= 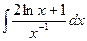 +С =2
+С =2 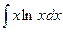 +
+ 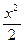 +С. Если учесть «табличный» интеграл (легко получить интегрированием по частям!):
+С. Если учесть «табличный» интеграл (легко получить интегрированием по частям!): 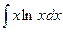 = =
= = 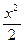 lnx–
lnx– 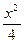 , то: v=x2lnx+
, то: v=x2lnx+ 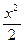 –
– 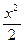 +С =x2lnx+С.
+С =x2lnx+С.
a3. Запишем общее решение уравнения: y=u∙v= 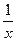 ∙
∙ 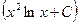 = xlnx +
= xlnx + 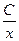 .
.
Ответ: y= xlnx + 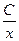 – общее решение.
– общее решение.
Пример 4–75: Решить дифференциальное уравнение: (1+ x2)dx=(arctgy–x)dy.
Решение:
1). Видим, что по y и y′ уравнение не приводится к линейному уравнению. Приведём уравнение к «стандартной форме» линейного по по x и x′: x′ + 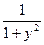 x =
x = 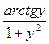 .
.
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: y=u∙v.
a1. Вычислим интеграл: – 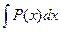 =–
=– 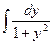 =– arctgy → u=
=– arctgy → u= 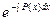 =
= 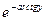 .
.
a2. Вычислим функцию v: v= 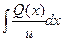 +С=
+С= 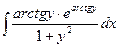 +С=[Примем: arctgy=t]= =
+С=[Примем: arctgy=t]= = 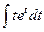 +С=[см. таблицу интегралов!]=tet–et+С= arctgy
+С=[см. таблицу интегралов!]=tet–et+С= arctgy 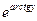 –
– 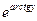 +С.
+С.
a3. Запишем общее решение уравнения: y=u∙v= 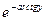 ∙
∙ 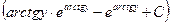 = =arctgy–1+C
= =arctgy–1+C 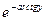
Ответ: y= arctgy–1+C 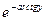 – общее решение.
– общее решение.
Пример 5–85: Решить дифференциальное уравнение: y′ = 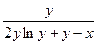 , y(1)=1.
, y(1)=1.
Решение:
1). Видим, что по y и y′ уравнение не приводится к линейному уравнению. Приведём уравнение к «стандартной форме» линейного по по x и x′: x′ + 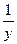 x =2lny+1.
x =2lny+1.
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде функции: x=u∙v.
a1. Вычислим интеграл: – 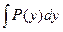 =–
=– 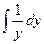 =– lny → u=
=– lny → u= 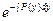 =
= 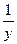 .
.
a2. Вычислим функцию v: v= 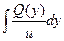 +С=
+С= 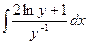 +С =2
+С =2 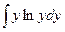 +
+ 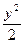 +С. Если учесть результат Примера 3–72, то: v= y2lny+С.
+С. Если учесть результат Примера 3–72, то: v= y2lny+С.
a3. Запишем общее решение уравнения: x=u∙v= 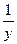 ∙(y2lny+С) = ylny +
∙(y2lny+С) = ylny + 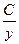 .
.
a4. Запишем частное решение уравнения: x = ylny + 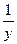 , так как С=1.
, так как С=1.
Ответ: x = ylny + 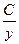 – общее решение; частное решение: x = ylny +
– общее решение; частное решение: x = ylny + 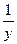 .
.
Пример 6–87: Решить дифференциальное уравнение: dy =(y2ex–y)dx. (1)
Решение:
1). Из исходного уравнения: y=0–решение. Перепишем (1): y′+y =ex∙y2. (2)
2). Получили уравнение (2) Бернулли в «стандартной форме», для n=2.
a0. Примем: z = y–n+1, где (–n+1)= –1; то есть: z= y–1.
a1. Запишем преобразованное уравнение Бернулли: z′–z= – ex. (3)
a2. Решение уравнения ищем в виде функции: z=u(x)∙v(x);
a3. Вычислим интеграл: – 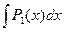 =
= 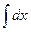 =x → u=
=x → u= 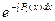 = ex.
= ex.
a4. Вычислим функцию v: v = 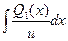 =
= 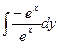 +С= – x +С;
+С= – x +С;
a5. Запишем общее решение уравнения для (3): z=u∙v= ex ∙( С–x). (4)
a6. Учитывая: z= y–1, запишем общее решение для (1): y–1=ex ∙( С–x).
Ответ: yex ∙( С–x)=1 – общее решение уравнения, также y=0.
Пример 7–89: Решить дифференциальное уравнение: y′ = yctgx+ 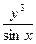 . (1)
. (1)
Решение:
1). Из исходного уравнения: y=0–решение. Перепишем (1): y′–ctgxy = 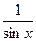 ∙y3. (2)
∙y3. (2)
2). Получили уравнение (2) Бернулли в «стандартной форме», для n=3.
a0. Примем: z = y–n+1, где (–n+1)= –2; то есть: z= y–2.
a1. Запишем преобразованное уравнение Бернулли: z′+ctgx∙z= –2 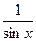 . (3)
. (3)
a2. Решение уравнения ищем в виде функции: z=u(x)∙v(x);
a3. Вычислим интеграл: – 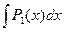 =–2
=–2 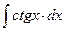 =–2ln|sinx| → u=
=–2ln|sinx| → u= 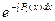 =
= 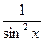 .
.
a4. Вычислим функцию v: v = 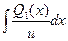 =
= 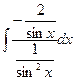 +С=–2
+С=–2 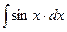 +С=2cosx+C;
+С=2cosx+C;
a5. Запишем общее решение уравнения для (3): z=u∙v= 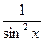 (2cosx+C). (4)
(2cosx+C). (4)
a6. Учитывая: z= y–2, запишем общее решение для (1): y–2= 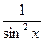 (2cosx+C).
(2cosx+C).
Ответ: sin2x= y2(2cosx+C) – общее решение уравнения, также y=0.
Пример 8–94: Решить дифференциальное уравнение: 3dy= –(1+3y3)y∙sinxdx, y 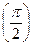 =1. (1)
=1. (1)
Решение:
1). Из исходного уравнения: y=0–решение. Перепишем (1): y′+ 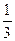 sinx∙y =–sinx∙y4. (2)
sinx∙y =–sinx∙y4. (2)
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Примем: z = y–n+1, где (–n+1)= –3; то есть: z= y–3.
a1. Запишем преобразованное уравнение Бернулли: z′–sinx∙z= 3sinx. (3)
a2. Решение уравнения ищем в виде функции: z=u(x)∙v(x);
a3. Вычислим интеграл: – 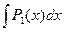 =
= 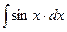 =–cosx → u=
=–cosx → u= 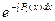 =e–cosx.
=e–cosx.
a4. Вычислим функцию v: v = 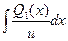 =
= 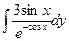 + С = –3
+ С = –3 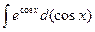 + С =
+ С =
=–3ecosx +С;
a5. Запишем общее решение уравнения для (3): z=u∙v= e–cosx (–3ecosx +С). (4)
a6. Учитывая: z= y–3, запишем общее решение для (1): y–3=Ce–cosx –3.
a4. Запишем частное решение уравнения: y–3=4e–cosx –3, так как С=4.
Ответ: y–3=Ce–cosx –3 – общее решение; частное решение: y–3=4e–cosx –3.
Пример 9–180: Найти уравнение кривой, проходящей через точку (0,1), если площадь треугольника, образуемого осью абсцисс, касательной и радиус-вектором точки касания, постоянна и равна 1.
Решение:
В Примере 1–19 получено выражение: отрезка Т=OТ= 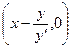 , – отсекаемого касательной на оси абсцисс.
, – отсекаемого касательной на оси абсцисс.
1). Так как площадь треугольника вычисляется по формуле: S= 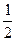 ah, где a–основание, h – высота треугольника, условие задачи запишем так:
ah, где a–основание, h – высота треугольника, условие задачи запишем так:
 ▪ ОТ∙ND=2S=2 →
▪ ОТ∙ND=2S=2 → 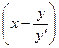 ∙y =2; (1)
∙y =2; (1)
▪ ОT∙ND=2S=–2 → 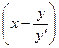 ∙y =–2 (2)
∙y =–2 (2)
Случай-1.
2). Запишем (1), в виде: x′– 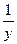 x=–
x=– 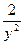 – «стандартная форма» линейного уравнения.
– «стандартная форма» линейного уравнения.
a0. Решение уравнения ищем в виде функции: x=u∙v.
a1. Вычислим интеграл: – 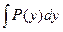 =
= 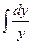 =ln|y| → u=y.
=ln|y| → u=y.
a2. Вычислим функцию v: v = 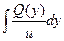 +С=–2
+С=–2 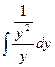 +С =y–2+С.
+С =y–2+С.
a3. Запишем общее решение уравнения: x=u∙v=y ∙(y–2+С)= 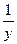 +Cy.
+Cy.
a4. Запишем частное решение уравнения: x= 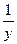 –y, при С=–1.
–y, при С=–1.
Случай-2.
3). Запишем (2), в виде: x′– 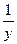 x=
x= 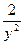 – «стандартная форма» линейного уравнения.
– «стандартная форма» линейного уравнения.
a0. Решение уравнения ищем в виде функции: x=u∙v.
a1. Вычислим интеграл: – 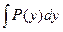 =
= 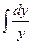 =ln|y| → u=y.
=ln|y| → u=y.
a2. Вычислим функцию v: v = 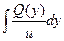 +С=2
+С=2 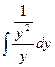 +С =–y–2+С;
+С =–y–2+С;
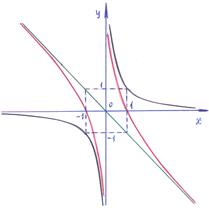 a3. Запишем общее решение уравнения: x=u∙v=y∙(С–y–2)=Cy–
a3. Запишем общее решение уравнения: x=u∙v=y∙(С–y–2)=Cy– 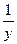 . Это решение «симметрично относительно оси ОХ» решению, полученному в Случае-1.
. Это решение «симметрично относительно оси ОХ» решению, полученному в Случае-1.
a4. Запишем частное решение уравнения: x=y– 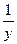 , при С=1.
, при С=1.
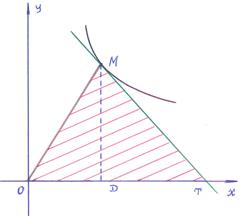
4). Построим эскиз графика функции x= 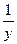 –y, используя известные графики для гиперболы и прямой и применяя понятие «сумма функций» (см. рисунок: выделено красным).
–y, используя известные графики для гиперболы и прямой и применяя понятие «сумма функций» (см. рисунок: выделено красным).
Ответ: для Случая-1: x= 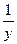 –y – частное решение ДУ; для Случая-2: x= y –
–y – частное решение ДУ; для Случая-2: x= y – 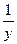 – частное решение ДУ.
– частное решение ДУ.
Замечание: Если не заметить присутствия двух различных вариантов решения рассмотренной задачи, то «зеркальное решение» будет потеряно. В задачах физики это дополнительно подсказывает важность понимания начальных условий исследуемого процесса: возможно исследователю потребуются дополнительные эксперименты для уточнения особенностей протекания процесса.
Пример 10–198: Сила тока i в цепи с сопротивлением R, индуктивностью L и напряжением u удовлетворяет уравнению: L∙ 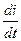 + R∙i = u. Найти силу тока i в момент времени t, если u= Esinωt и i = 0 при t = 0 (L, R, E, ω – постоянные).
+ R∙i = u. Найти силу тока i в момент времени t, если u= Esinωt и i = 0 при t = 0 (L, R, E, ω – постоянные).
Решение:
 1). Приведём уравнение к «стандартной форме»:
1). Приведём уравнение к «стандартной форме»:
i′ + a∙i = b∙u: (1)
где a= 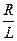 и b=
и b= 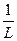 (принято для удобства записи).
(принято для удобства записи).
2). Данное уравнение решаем, применяя общий алгоритм:
a0. Решение уравнения ищем в виде: функцию i=z∙v.
a1. Вычислим интеграл: – 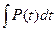 =–a
=–a 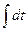 =–at → z=
=–at → z= 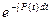 =e–at.
=e–at.
a2. Вычислим функцию v: v= 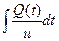 +С=b
+С=b 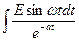 +С=bE
+С=bE 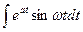 +С. Вычислим интеграл: J=
+С. Вычислим интеграл: J= 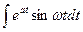 =[дважды применяется «интегрирование по частям», затем решение алгебраического равенства относительно символа J]=
=[дважды применяется «интегрирование по частям», затем решение алгебраического равенства относительно символа J]= 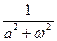 eat∙(a∙sinωt–ω∙cosωt). Тогда окончательно: v=bE∙J+С, или v=bE∙J+bE∙С=bE∙(J+С). Последнее определяется «удобством!»: допустимо, так как bE – постоянная величина!
eat∙(a∙sinωt–ω∙cosωt). Тогда окончательно: v=bE∙J+С, или v=bE∙J+bE∙С=bE∙(J+С). Последнее определяется «удобством!»: допустимо, так как bE – постоянная величина!
a3. Запишем общее решение уравнения: i=u∙v=bE∙e–at∙(J+С). (2)
a4. Запишем частное решение уравнения из условия: i(0)=0 → легко вычисляется С= 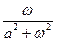 → частное решение: i=bE∙
→ частное решение: i=bE∙ 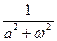 (a∙sinωt–ω∙cosωt+ω∙e–at). С учетом значений a и b получим окончательно: i=
(a∙sinωt–ω∙cosωt+ω∙e–at). С учетом значений a и b получим окончательно: i= 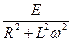 (R∙sinωt–Lω∙cosωt+Lω∙
(R∙sinωt–Lω∙cosωt+Lω∙ 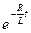 ).
).
Ответ: i= 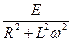 (R∙sinωt–Lω∙cosωt+Lω∙
(R∙sinωt–Lω∙cosωt+Lω∙ 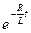 ) – частное решение.
) – частное решение.
☻
Вопросы для самопроверки:
1. Как определяют линейное дифференциальное уравнение 1-го порядка?
2. Что значит: «стандартная форма» линейного уравнения, зачем её вводят?
3. Какова основная «идея» способа «подстановки» решения линейного уравнения?
4. Всегда ли можно «проинтегрировать» линейное ДУ?
5. Какие уравнения относят к уравнениям Бернулли?
6. В чем особенность интегрирования уравнения Бернулли?
7. Бывают ли уравнения Бернулли, которые невозможно «проинтегрировать»?
< * * * * * >
