Числовые ряды. Признаки сходимости рядов с положительными членами. Знакопеременные ряды.

Пусть задана бесконечная последовательность вещественных чисел 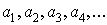Построим последовательность: 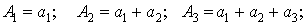… 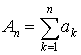и рассмотрим предел этой последовательности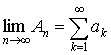

Он называется числовым рядом, или просто рядом. Если этот предел существует и конечен, то говорят, что ряд сходится, или, что ряд существует. Если этот предел равен бесконечности или вообще не существует, то говорят, что ряд расходится, или, что ряд не существует.

Величины A_n называются частными суммамиряда. Слагаемое a_n называется общим членомряда. Ряды 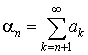называются остаткомряда после n-го слагаемого.

Простейшие свойства сходящихся рядов.

1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числачленов ряда не изменяет его сходимости или расходимости.

2. Если ряд 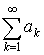сходится, то .

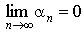3. Если ряд 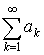сходится, то сходится ряд 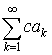и имеет место равенство .

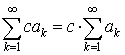4. Если ряды 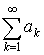и 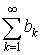сходятся, то сходится и ряд 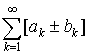имеет место равенство

.

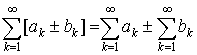5. Если ряд 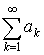сходится, то 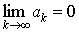. Отсюда следует

Признак расходимости ряда. Если 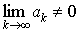, то ряд 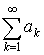расходится.

Признаки сходимости рядов с положительными членами

Пусть дан ряд 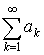все слагаемые которого положительны .

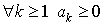Признак Коши. Пусть существует 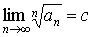. Тогда

если 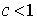, то ряд 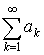сходится; если 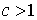, то ряд 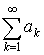расходится;

если 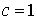, то о сходимости или расходимости ряда ничего сказать нельзя.

Признак Даламбера.Пусть существует 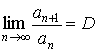. Тогда

если 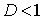, то ряд 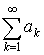сходится; если 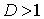, то ряд 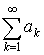расходится;

если 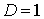, то о сходимости или расходимости ряда ничего сказать нельзя.

Интегральный признак Коши

Пусть f(x) – некоторая функция, определенная на интервале [1, ). Здесь рассматриваются ряды вида 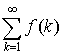, то есть ряды со слагаемыми вида .

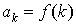Интегральный признак Коши.Пусть при x функция f(x) монотонноубывает до нуля, то есть 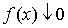. Тогда ряд 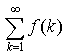сходится или расходится одновременно с интегралом .

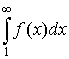Знакопеременные ряды Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.

Признак ЛейбницаДля знакочередующихся рядом действует достаточный признак сходимости Лейбница. Пусть {an} является числовой последовательностью, такой, чтоan+1<an для всех n;

limn→∞an=0.

Тогда знакочередующиеся ряды ∞∑n=1(−1)nan и ∞∑n=1(−1)n−1an сходятся.

Абсолютная и условная сходимость

Ряд ∞∑n=1an называется абсолютно сходящимся, если ряд ∞∑n=1|an| также сходится.
Если ряд ∞∑n=1an сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.
Ряд ∞∑n=1an называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.