Поле комплексных чисел. Действия над комплексными числами. Методы.

Опр. Системой компл-х чисел наз-ся мин-ое поле, которое яв-ся расширением поля действительных чисел и в котором есть элемент i (i²-1=0)

Опр. Алгебра <ℂ, +, ∙, 0, 1, ℝ, ⊕, ⊙, i> наз-ся сис-ой комп-х чисел, если вып-ся следующие условия (аксиомы):

1. 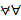a,b∊ℂ∃!m∊ℂ: a+b=m

2. 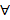a,b,c∊ℂ (a+b)+c=a+(b+c)

3. 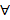a,b∊ℂa+b=b+a

4. ∃ 0∊ℂ 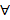a∊ℂ a+0=a

5. 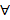a∊ℂ ∃(-a)∊ℂ a+(-a)=0

6. 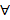a,b∊ℂ ∃! n∊ℂa∙b=n

7. 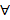a,b,c∊ℂ (a∙b)∙c=a∙(b∙c)

8. 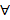a,b∊ℂa∙b=b∙a

9. ∃1∊ℂ 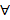a∊ℂ a∙1=a

10. 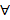a∊ℂ ∃a^-1∊ℂ a∙a^-1=1

11. 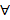a,b,c∊ℂ (a+b)c=ac+bc

12. <R,⊕,⊙>-поле действ. чисел

13. Rєℂ, 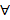a,b∊R a⊕b=a+b, a⊙b=a∙b

14. ∃i∊ℂ:i²+1=0

15. 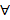ℳ≠⌀ 1)ℳ⊂ℂ,R⊂ℳ 2) 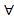α,β∊ℳ⇒(α+β)∊ℳ и (α∙β)∊ℳ}⇒ℳ=ℂ

Св-ва ℂ чисел:

1. 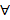α∊ℂ∃! (a,b) ∊ R:α=a+b∙i

2. Поле комп-х чисел нельзя линейно упорядочить т.е. 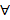α∊ℂ, α≥0 |+1, α²+1≥1, i²+1=0, 0≥1-невозможно.

3. Основная теорема алгебры: Поле ℂ чисел алгебраически замкнуто, то есть любой мн-н полож. степени над полем ℂ чисел имеет хотя бы один компл. корень

След-е из осн. теоремы алг.: Любой мн-н полож. степени над полем комплексных чисел можно разл-ть на произведение … первой степени с положительным коэффициентом.

След-е: любое квад-е ур-е имеет 2-а корня: 1) D>0 2-а разл. действ. корня 2)D=0 2-а деств. совп-х корня 3)D<0 2-а компл-х корня.

4. Аксиом. теория комплексных чисел категорична и непротиворечива

Методика.

В общеобразовательных классах не рассматривается понятие комплексного числа, ограничиваются лишь изучением действительных чисел. Но в старших классах школьники уже обладают достаточно зрелым математическим образованием и в состоянии понимать необходимость расширения понятия о числе. С точки зрения общего развития, знания о комплексных числах находят применение в естественных науках и технике, что немаловажно для школьника в процессе выбора будущей профессии. Авторы некоторых учебников включают изучение данной темы как обязательной в свои учебники по алгебре и началам математического анализа для профильных уровней, что предусмотрено государственным стандартом.

С методической точки зрения тема “Комплексные числа” развивает и углубляет заложенные в основном курсе математики представления о многочленах и числах, в известном смысле завершая путь развития понятия числа в средней школе.

Однако даже в старших классах у многих школьников плохо развито абстрактное мышление, или очень сложно представить себе «мнимую, воображаемую» единицу, понять различия между координатной и комплексной плоскостью. Или же наоборот, школьник оперирует абстрактными понятиями в отрыве от их реального содержания.

После изучения темы “Комплексные числа” ученики должны иметь четкое представление о комплексных числах, знать алгебраическую, геометрическую и тригонометрическую формы комплексного числа. Учащиеся должны уметь производить над комплексными числами операции сложения, умножения, вычитания, деления, возведения в степень, извлечения корня из комплексного числа; переводить комплексные числа из алгебраической формы в тригонометрическую, иметь представление о геометрической модели комплексных чисел

В учебнике для математических классов Н.Я.Виленкина, О.С.Ивашева-Мусатова, С.И.Шварцбурда «Алгебра и начала математического анализа», тема «Комплексные числа» вводится в 11 классе. Изучение темы предлагается во втором полугодии 11 класса после того, как в 10 классе был изучен раздел тригонометрии, а в 11 - интеграл и дифференциальные уравнения, показательная, логарифмическая и степенная функции, многочлены. В учебнике тема «Комплексные числа и операции над ними» разбита на два параграфа: Комплексные числа в алгебраической форме; Тригонометрическая форма комплексных чисел. Рассмотрение темы «Комплексные числа и операции над ними» начинается с рассмотрения вопроса о решении квадратных уравнений, уравнений третьей и четвертой степени и, как следствие, выявляется необходимость введения «нового числа i». Сразу же даются понятия комплексных чисел и действий над ними: нахождение суммы, произведения и частного комплексных чисел. Далее дается строгое определение понятия комплексного числа, свойства операций сложения и умножения, вычитания и деления. В следующем пункте говорится о сопряженных комплексных числах и некоторых их свойствах. Далее рассматривается вопрос об извлечении квадратных корней из комплексных чисел и решение квадратных уравнений с комплексными коэффициентами. В следующем параграфе рассматриваются: геометрическое изображение комплексных чисел; полярная система координат и тригонометрическая форма комплексных чисел; умножение, возведение в степень и деление комплексных чисел в тригонометрической форме; формула Муавра, применение комплексных чисел к доказательству тригонометрических тождеств; извлечение корня из комплексного числа; основная теорема алгебры многочленов; комплексные числа и геометрические преобразования, функции комплексного переменного.

В учебнике С.М. Никольского, М.К. Потапова, Н.Н. Решетникова, А.В. Шевкина «Алгебра и начала математического анализа», тема «Комплексные числа рассматривается в 11 классе после изучения всех тем, т.е. в конце школьного курса алгебры. Тема разделена на три параграфа: Алгебраическая форма и геометрическая интерпретация комплексных чисел; Тригонометрическая форма комплексных чисел; Корни многочленов, показательная форма комплексных чисел. Содержание параграфов достаточно объемное, содержится много понятий, определений, теорем. В параграфе «Алгебраическая форма и геометрическая интерпретация комплексных чисел» содержится три раздела: алгебраическая форма комплексного числа; сопряженные комплексные числа; геометрическая интерпретация комплексного числа. Параграф «Тригонометрическая форма комплексного числа» содержит определения и понятия необходимые для введения понятия тригонометрической формы комплексного числа, а также алгоритм перехода от алгебраической формы записи к тригонометрической форме записи комплексного числа. В последнем параграфе «Корни многочленов. Показательная форма комплексных чисел» содержится три раздела: корни из комплексных чисел и их свойства; корни многочленов; показательная форма комплексного числа.

Материал учебника представлен в небольшом объеме, но вполне достаточном для понимания учащимися сути комплексных чисел и овладением минимальных знаний о них. В учебнике небольшое количество упражнений и не рассматривается вопрос о возведении комплексного числа в степень и формула Муавра

В учебнике А.Г. Мордковича, П.В. Семенова «Алгебра и начала математического анализа», профильный уровень, 10 класс тема «Комплексные числа» вводится во втором полугодии 10 класса сразу после изучения тем «Действительные числа» и «Тригонометрия». Такое размещение не случайно: и числовая окружность, и формулы тригонометрии находят активное применение при изучении тригонометрической формы комплексного числа, формулы Муавра, при извлечении из комплексного числа квадратного и кубического корней. Тема «Комплексные числа» представлена в 6-ой главе и разбита на 5 параграфов: комплексные числа и арифметические операции над ними; комплексные числа и координатная плоскость; тригонометрическая форма записи комплексного числа; комплексные числа и квадратные уравнения; возведение комплексного числа в степень, извлечение кубического корня из комплексного числа.

Понятие комплексного числа вводится как расширение понятия о числе и невозможности выполнения некоторых действий в действительных числах. В учебнике представлена таблица с основными числовыми множествами и операциями, допустимыми в них. Перечисляются минимальные условия, которым должны удовлетворять комплексные числа, и затем вводится понятие мнимой единицы, определение комплексного числа, равенство комплексных чисел, их сумма, разность, произведение и частное.

От геометрической модели множества действительных чисел переходят к геометрической модели множества комплексных чисел. Рассмотрение темы «Тригонометрическая форма записи комплексного числа» начинается с определения и свойств модуля комплексного числа. Далее рассматривается тригонометрическая форма записи комплексного числа, определение аргумента комплексного числа и стандартная тригонометрическая форма комплексного числа.

Далее изучается извлечение квадратного корня из комплексного числа, решение квадратных уравнений. И в последнем параграфе вводится формула Муавра и выводится алгоритм извлечения кубического корня из комплексного числа.

Также в рассматриваемом учебнике в каждом параграфе параллельно с теоретической частью рассматривается несколько примеров, иллюстрирующих теорию и дающих более осмысленное восприятие темы. Приведены краткие исторические факты.