Кольцо целых чисел. Теорема о делении с остатком. НОК и НОД чисел. Методика.

Опр. Кольцо K называется кольцом целых чисел, если аддитивная группа кольца K является аддитивной группой целых чисел и умножение в кольце K коммутативно и продолжает умножение натуральных чисел (в системе N натуральных чисел).

Т1.Пусть <Z, +, -> - аддитивная группа целых чисел, есть естественное умножение в ней и 1 – единица системы N натуральных чисел. Тогда алгебра Z=<Z,+,-,*,1>является кольцом целых чисел.

Док-во. Покажем, что алгебра Z есть коммутативное кольцо. По условию, алгебра <Z, +, -> - аддитивная группа кольца – есть абелева группа, как аддитивная группа целых чисел.

Пусть a, b, c – произвольные элементы множества Z. Их можно представить в виде радости натуральных чисел. Пусть (1) a=m-n, b=p-q, c=r-s (m, n, p, q, r, s 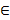N).

Естественное умножение в Z определяется формулой (2) a*b=(m-n)*(p-q)=(mp+nq)-(mq+np).

Естественное умножение коммутативно, так как b*a= (p-q)*(m-n)=(pm+qn)-(pn+qm), и коммутативно сложение и умножение натуральных чисел.

Естественное умножение ассоциативно. В самом деле, в силу (1) и (2) имеем:

a*(b*c)=(m-n)[(p-q)(r-s)]=(m-n)[(pr+qs)-(ps-qr)]=(mpr+mqs+nps+nqr)-(mps+mqr+npr+nqs);

(a*b)*c=[(m-n)(p-q)](r-s)=[(mp+nq)-(mq+np)](r-s)=(mpr+nqr+mqs+nps)-(mps+nqs+mqr+npr).

Следовательно, в силу коммутативности сложения натуральных чисел a*(b*c)= (a*b)*c.

Элемент 1 является нейтральным относительно естественного умножения. В самом деле, для любого a из 2 имеем a*1=(m-n)(1-0)=m*1-n*1=m-n=a.

Следовательно, алгебра <Z,*,1>является коммутативным моноидом.

Опр. Если для целых чисел aи bсуществует такое натуральное число k, что a+k=bи k 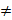0,то говорят, что «a меньше или b», и пишут a<b. Говорят, что «aменьше или равно b», и пишут a≤b, если a<bили a=b. a>b тогда и только тогда, когда b<a.

Т2. Пусть Z=<Z, +, -, *, 1>кольцо целых чисел. Тогда: 1) для любых целых чисел a и b выполняется одно и только одно из трех услоий: a<b, a=b, b<a.

2) для любого целого числа a выполняется одно и только одно из трех условий: a<0, a=0, 0<a;

3) отношение < монотонно относительно сложения, т.е. для любых целых a, bи c

a<bтогда и только тогда, когда a+c<b+c;

4) отношение <монотонно относительно умножения, т.е. для любых целых a, bи с

если a<bи c>0, то ac<bc.

Т. о делении с остатком. Пусть a – целое число и b – натуральное число, отличное от нуля. Разделить число a и b с остатком – значит представить его в виде a=bq+r, где 0 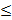r<b, q и r – целые числа. При этом q называется неполным частным, а число r – остатком от деления aна b.

Деление с остатком всегда выполнимо, а неполное частное и остаток однозначно определяются делимым и делителем.

Т. Для любых целых чисел a, bпри b>0существует единственная пара целых чисел qи r, удовлетворяющая условиям: (1) a=bq+rи 0 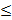r<b.

Док-во. Докажем, что существует хотя бы одна пара чисел q, r удовлетворяющая условиям (1). Вначале рассмотрим случай, когда a – натуральное число. Фиксируем b и индукцией по a докажем, что (2) существует пара целых чисел q, r, удовлетворяющая (1).

Для a=0 утверждение (2) верно, так как 0=b*0+0. Предположим, что (2) верно для a=n, т.е. существуют целые q, rтакие, что (3) n=bq+rи 0 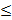r<b, и докажем, что оно верно для a=n+1. Из (3) следует n+1=bq+(r+1) и 0<r+1 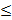b. Если r+1<b, то пара чисел q, r+1 является искомой. Если же r+1=b, то n+1=b(q+1) и пара чисел q+1, 0 является искомой.

Наибольший общий делитель. Целое число c называется общим делителем целых чисел a₁, …, a_n, если cесть делитель каждого из этих чисел.

Опр. Наибольшим общим делителем целых чисел a₁, …, a_n называется такой их общий делитель, который делится на любой общий делитель этих чисел.

Целые числа a₁, …, a_n называется взаимно простыми, если их наибольший общий делитель чисел равен единице.

НОД чисел a₁, …, a_n обозначается НОД(a₁, …, a_n), положительный НОД этих чисел обозначается нод(a₁, …, a_n).

След-ие 1. Если d есть НОД целых чисел a₁, …, a_n, то множество всех общих делителей этих чисел совпадает с множеством всех делителей числа d.

След-ие 2. Любые два НОД целых чисел a₁, …, a_n ассоциированы, т.е. могут отличаться только знаком. Если d есть НОД чисел a₁, …, a_n, то число (-d) также есть НОД этих чисел.

Алгоритм Евклида. Способ нахождения НОД двух целых чисел.

Предложение. Пусть aи b–два целых числа, b≠0 и (1) a=bq+r (0 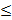r<|b|).

Тогда нод(a,b)=нод(b,r).

Док-во. Из (1) следует, что любой общий делитель чисел aи bесть делитель числа r=a-bqи любой общий делитель чисел bи rесть делитель числа a. Поэтому множество всех общих делителей чисел aи bсовпадает с множеством всех общих делителей чисел bи r. Отсюда следует, что положительный общий делитель чисел aи bсовпадает с положительным общим делителем чисел bи r, т.е. нод(a,b)=нод(b,r).

Если b|a, где b≥1, то очевидно, нод(a,b)=b. Для нахождения нод двух целых чисел применяют способ «последовательного деления», называемый алгоритмом Евклида. Сущность этого способа состоит в том, что в силу доказанного выше предложения задача нахождения нод чисел a и bсводится к более простой задаче нахождения нод чисел bи r, где 0≤r<|b|. Если r=0, то нод(a,b)=b. Если же r≠0, то рассуждения повторяем, отправляясь от bи r. В результате получим цепочку равенств.

Если a=0, то b=0*c=0 и теорема верна. Если же a≠0, то из (1) следует cd=1. По теореме, из равенства cd=1 следует, что d= 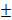1. Кроме того, a=bd; следовательно, a= 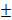b. Доказано.

Наименьшее общее кратное. Целое число cназывается общим кратным целых чисел a₁, …, a_n, если оно делится на каждое из этих чисел.

Опр. Наименьшим общим кратным целых чисел a₁, …, a_nназывается такое их общее кратное, которое делит любое общее кратное этих чисел. Об-ие: НОК(a₁, …, a_n). Положительное наименьшее общее кратное чисел a₁, …, a_n, отличных от нуля, об-ся через [a₁, …, a_n].

Сл-ие. Любые два наименьших общих кратных целых чисел a₁, …, a_n ассоциированы в Z, т.е. могут отличаться только знаком. Если число mесть НОК(a₁, …, a_n), то и число (-m) есть НОК(a₁, …, a_n).

Сл-ие. Если m – наименьшее общее кратное чисел a₁, …, a_n, то множество всех общих кратных этих чисел совпадает с множеством всех кратных числа m.