Основные методы интегрирования (метод интегрирования по частям).
Пусть u=u(x) и u=v(x) –ф-ии, имеющие непрерывные производные. Тогда d(uv)=u·dv+v·du. Интегрируя это равенство, получим ∫d(uv)=∫u·dv+∫v·du или ∫u·dv=uv-∫v·du - формула интегрирования по частям.
Формула интегрирования по частям применяется в случае, когда под знаком интеграла стоит произв-е функций из разных классов.
Очень важно грамотно взять u и dv.
1. Если под знаком интеграла стоит произ-е обратнотригонометрических функций, то за u берут именно эти функции.
2. Если интеграл не содержит выше перечисленных два класса, то за u берут степенную функцию.
3. Если интеграл содержит произ-е показательной функции на тригонометрическую, то нет разницы что брать за u. Но формула интегрирования по частям должна быть применена дважды и каждый раз за u берем одну и ту же функцию.
51.Простейшие дроби 4 типов. Дробь вида 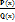 , где Pn(x) и Qm(x) являются многочленами степени n и m, называется рациональной. Если показатель степени числителя больше показателя степенизнаменателя, то дробь называется неправильной, в противном случае — правильной. Всякую правильную рациональную дробь можно представить в виде суммы конечного числа так называемых простейших дробей следующих 4 типов:
, где Pn(x) и Qm(x) являются многочленами степени n и m, называется рациональной. Если показатель степени числителя больше показателя степенизнаменателя, то дробь называется неправильной, в противном случае — правильной. Всякую правильную рациональную дробь можно представить в виде суммы конечного числа так называемых простейших дробей следующих 4 типов: 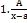 ; 2.
; 2. 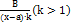 ; 3.
; 3. 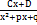 ; 4.
; 4. 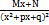 . Любую правильную рациональную функцию можно представить в виде суммы простейших дробей. Тип простейшей дроби и количество определяется по знаменателю исходной дроби. Коэффициенты, стоящие в правой части A,B,C,D,M,Nнаходятся следующим образом: 1.Правую часть приводят к общему знаменателю, который равен знаменателю исходной дроби. 2. Из равенства двух дробей с одинаковыми знаменателями заключаем равенство числителей (приравниваем числители) 3. Так как два многочлена равны, тогда когда равны их коэффициенты при , соответсвующих степенях X приравниваем эти коэффициенты в обеих частях.
. Любую правильную рациональную функцию можно представить в виде суммы простейших дробей. Тип простейшей дроби и количество определяется по знаменателю исходной дроби. Коэффициенты, стоящие в правой части A,B,C,D,M,Nнаходятся следующим образом: 1.Правую часть приводят к общему знаменателю, который равен знаменателю исходной дроби. 2. Из равенства двух дробей с одинаковыми знаменателями заключаем равенство числителей (приравниваем числители) 3. Так как два многочлена равны, тогда когда равны их коэффициенты при , соответсвующих степенях X приравниваем эти коэффициенты в обеих частях.
52.Интегрирование рациональных функций. Для интегрирования рациональной функции P(x)Q(x), где P(x) и Q(x) − полиномы, используется следующая последовательность шагов: 1) Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение; 2) Разложить знаменатель Q(x) на произведение одночленов или несократимых квадратичных выражений; 3)Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов 4) Вычислить интегралы от простейших дробей.
53.ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ . 1). Интегралы вида: 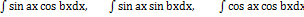 находятся с помощью тригонометрических формул:
находятся с помощью тригонометрических формул: 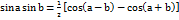
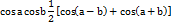
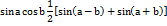
2)Интегралы вида: 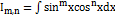 где m и n - четные числа находятся с помощью формул понижения степени
где m и n - четные числа находятся с помощью формул понижения степени
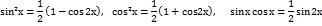
Если хотя бы одно из чисел m или n - нечетное, то полагают: 
54. Интегрирование простейших иррациональных функций. Используя метод непосредственного интегрирования, достаточно просто находятся неопределенные интегралы вида 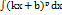 , где p – рациональная дробь, k и b – действительные коэффициенты.Бывают случаи, когда уместно использование метода подведения под знак дифференциала. Например, при нахождении неопределенных интегралов вида
, где p – рациональная дробь, k и b – действительные коэффициенты.Бывают случаи, когда уместно использование метода подведения под знак дифференциала. Например, при нахождении неопределенных интегралов вида 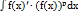 , где p – рациональная дробь.Достаточно часто приходится иметь дело с неопределенными интегралами вида
, где p – рациональная дробь.Достаточно часто приходится иметь дело с неопределенными интегралами вида 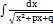 , где p и q – действительные коэффициенты.В этом случае выделяем полный квадрат под знаком корня:
, где p и q – действительные коэффициенты.В этом случае выделяем полный квадрат под знаком корня: 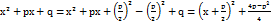 и используем формулу из таблицы неопределенных интегралов:
и используем формулу из таблицы неопределенных интегралов: 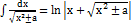 +C Аналогично проводится интегрирование иррациональных функций вида:
+C Аналогично проводится интегрирование иррациональных функций вида: 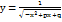 Нахождение множества первообразных иррациональных функций:
Нахождение множества первообразных иррациональных функций: 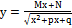 ,где M, N, p и q – действительные коэффициенты, очень схоже с интегрированием простейших дробей третьего типа: выполняется подведение под знак дифференциала, затем выделяется полный квадрат подкоренного выражения и применяются формулы из таблицы первообразных.Неопределенные интегралы иррациональных функций вида:
,где M, N, p и q – действительные коэффициенты, очень схоже с интегрированием простейших дробей третьего типа: выполняется подведение под знак дифференциала, затем выделяется полный квадрат подкоренного выражения и применяются формулы из таблицы первообразных.Неопределенные интегралы иррациональных функций вида: 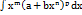 , находятся методом подстановки. В зависимости от рациональных чисел m, n и p вводят следующие новые переменные:1.Если p - целое число, то пимают
, находятся методом подстановки. В зависимости от рациональных чисел m, n и p вводят следующие новые переменные:1.Если p - целое число, то пимают 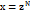 , где N - общий знаменатель чисел m и n. 2.Если
, где N - общий знаменатель чисел m и n. 2.Если 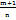 - целое число, то
- целое число, то 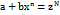 где N - знаменатель числа p.3.Если
где N - знаменатель числа p.3.Если 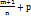 - целое число, то вводят новуюпеременную
- целое число, то вводят новуюпеременную 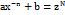 , где N - знаменатель числа p.
, где N - знаменатель числа p.
55.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ ИНТЕГРАЛЬНОЙ СУММЫПусть на отрезке [ab] дана непрерывная функция y=f(x). Необходимо найти площадькриволинейной трапеции (криволинейная трапеция- часть плоскости, заключенная междуграфиком функции, осью ОХ и вертикальными прямыми х=а и х=b).Разобьем отрезок [ab] на n отрезков точками 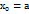 ,
, 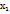 ,
, 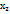 ……..
…….. 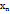 =b. Длина каждого из отрезков будет равна: ∆x=
=b. Длина каждого из отрезков будет равна: ∆x= 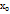 -
- 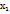 ,….,∆
,….,∆ 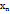 =
= 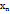 -
- 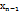 .Внутри каждого отрезка разбиения возьмем точки
.Внутри каждого отрезка разбиения возьмем точки 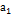 ,
, 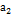 …..
….. 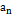 и вычислим значения функции в этих точках: f(
и вычислим значения функции в этих точках: f( 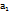 ), f(
), f( 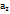 ),….., f(
),….., f( 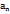 ). Составим сумму площадей полученных прямоугольников:
). Составим сумму площадей полученных прямоугольников: 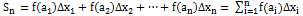 .Сумма (1) называется интегральной суммой функции y=f(x) на отрезке [a,b] ипредставляет собой сумму площадей всех прямоугольников.Определенным интегралом от функции y=f(x) на отрезке [a,b] называется пределинтегральной суммы (1), когда число участков разбиения стремится к бесконечности, адлина каждого из них стремится к нулю:
.Сумма (1) называется интегральной суммой функции y=f(x) на отрезке [a,b] ипредставляет собой сумму площадей всех прямоугольников.Определенным интегралом от функции y=f(x) на отрезке [a,b] называется пределинтегральной суммы (1), когда число участков разбиения стремится к бесконечности, адлина каждого из них стремится к нулю: 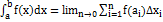 Где a и b называются пределами интегрирования, причем а – нижний пределинтегрирования, а b – верхний предел интегрирования.
Где a и b называются пределами интегрирования, причем а – нижний пределинтегрирования, а b – верхний предел интегрирования.
56.Теорема существования определенного интеграла. Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема по этому отрезку. Примем это утверждение без доказательства, поясним только его смысл. Интегрируемость функции означает существование конечного предела последовательности интегральных сумм, т.е. такого числа 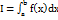 , что для любого
, что для любого 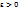 найдётся такое число
найдётся такое число 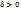 , что независимо от выбора точек выполняется неравенство
, что независимо от выбора точек выполняется неравенство 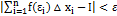 Требование непрерывности f(x) достаточно для интегрируемости, но не является необходимым. Интегрируемы функции, имеющие конечное или даже счётное число точек разрыва на [a,b] при условии их ограниченности (т.е. все точки разрыва должны быть точками разрыва первого рода). Неограниченная функция не может быть интегрируемой (идея доказательства этого утверждения: если f(x) неограничена на [a,b], то она неограничена на каком-либо [
Требование непрерывности f(x) достаточно для интегрируемости, но не является необходимым. Интегрируемы функции, имеющие конечное или даже счётное число точек разрыва на [a,b] при условии их ограниченности (т.е. все точки разрыва должны быть точками разрыва первого рода). Неограниченная функция не может быть интегрируемой (идея доказательства этого утверждения: если f(x) неограничена на [a,b], то она неограничена на каком-либо [ 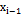 ,
, 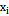 ], т.е. на этом отрезке можно найти такую точку
], т.е. на этом отрезке можно найти такую точку 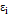 , что слагаемое
, что слагаемое 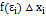 , а следовательно, и вся интегральная сумма, будет больше любого наперед заданного числа).
, а следовательно, и вся интегральная сумма, будет больше любого наперед заданного числа).
57. Геометрический смысл определенного интегралаOпределенный интеграл 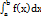 для непрерывной и неотрицательной функции y = f(x) представляет собой в геометрическом смысле площадь соответствующей криволинейной трапеции. В этом и состоит геометрический смысл определенного интеграла.То есть, вычислив определенный интеграл
для непрерывной и неотрицательной функции y = f(x) представляет собой в геометрическом смысле площадь соответствующей криволинейной трапеции. В этом и состоит геометрический смысл определенного интеграла.То есть, вычислив определенный интеграл 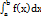 , мы найдем площадь фигуры, ограниченной линиями y = f(x), y = 0, x = a и x = b.Геометрический смысл определенного интеграла
, мы найдем площадь фигуры, ограниченной линиями y = f(x), y = 0, x = a и x = b.Геометрический смысл определенного интеграла 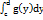 состоит в том, что его значение равно площади криволинейной трапеции для непрерывной и неотрицательной функции x=g(y) на отрезке [c;d]. Также справедливо
состоит в том, что его значение равно площади криволинейной трапеции для непрерывной и неотрицательной функции x=g(y) на отрезке [c;d]. Также справедливо 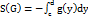 для непрерывной и неположительной функции x=g(y) на отрезке [c;d].
для непрерывной и неположительной функции x=g(y) на отрезке [c;d].
58.Основные свойства определенного интеграла.I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. 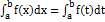 , где х, t – любые буквы.II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
, где х, t – любые буквы.II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю. 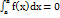 .III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
.III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный. 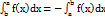 .IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
.IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам. 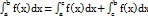 . V. Постоянный множитель можно выносить за знак определенного интеграла.
. V. Постоянный множитель можно выносить за знак определенного интеграла. 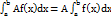 VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций. 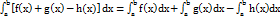
59.Оценка определенного интеграла. Теорема о среднемЕсли функция f(x) непрерывна на отрезке [a ;b],то найдётся такая точка ξ ∈ [a; b], что справедливо равенство 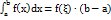 ,называемое формулой среднего значения.Величина
,называемое формулой среднего значения.Величина 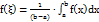 называется средним значением функции f(x) на отрезке [a b ]. Следствие теоремы о среднем. Оценка интеграла: если
называется средним значением функции f(x) на отрезке [a b ]. Следствие теоремы о среднем. Оценка интеграла: если 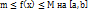 , то
, то 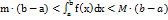 .
.
60. ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. Эта формула (называемая формулой Ньютона-Лейбница) сводит вопрос о вычислении определенного интеграла любой непрерывной функции к нахождению для нее первообразной функции. По существу этим перекинут мост между двумя частями математического анализа - дифференциальным исчислением (к которому, собственно, надо отнести и понятие первообразной функции) и интегральным исчислением, которое изучает в основном пределы интегральных сумм. К концу XVII в. оба эти исчисления были разработаны уже весьма обстоятельно, но то, что они связаны между собой, еще не было выяснено. Заслугой Ньютона и Лейбница является именно установление факта этой связи. Видим, что в основе ее лежит предложение, составляющее содержание теоремы, почему мы и назвали эту теорему основной теоремой математического анализа. Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедлива формула Ньютона-Лейбница: 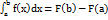 . Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления.Для доказательства формулы Ньютона-Лейбница нам потребуется понятие интеграла с переменным верхним пределом.Если функция y = f(x) непрерывна на отрезке [a; b], то для аргумента
. Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления.Для доказательства формулы Ньютона-Лейбница нам потребуется понятие интеграла с переменным верхним пределом.Если функция y = f(x) непрерывна на отрезке [a; b], то для аргумента 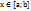 интеграл вида
интеграл вида 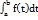 является функцией верхнего предела. Обозначим эту функцию
является функцией верхнего предела. Обозначим эту функцию 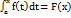 , причем эта функция непрерывная и справедливо равенство:
, причем эта функция непрерывная и справедливо равенство: 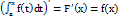 .Действительно, запишем приращение функции F(x), соответствующее приращению аргумента
.Действительно, запишем приращение функции F(x), соответствующее приращению аргумента 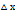 и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства: F
и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства: F 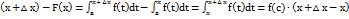 =
= 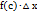 , где
, где 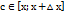 .Для применения формулы Ньютона-Лейбница нам достаточно знать одну из первообразных y=F(x) подынтегральной функции y=f(x) на отрезке [a; b] и вычислить приращение этой первообразной на этом отрезке
.Для применения формулы Ньютона-Лейбница нам достаточно знать одну из первообразных y=F(x) подынтегральной функции y=f(x) на отрезке [a; b] и вычислить приращение этой первообразной на этом отрезке
61. Интегрирование подстановкой (заменой переменной) в определенном интеграле ТЕОРЕМА. Пусть функция 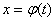 определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формулаТогда справедливо следующее равенство:
определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формулаТогда справедливо следующее равенство: 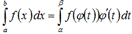 .Эта формула носит название формулы замены переменной в определенном интеграле. Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).
.Эта формула носит название формулы замены переменной в определенном интеграле. Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).
62. Интегрирование по частям в определенном интеграле Интегрирование по частям- один из способов нахождения интеграла. Суть метода в следующем: если подинтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композиции ), то справедливы следующие формулы:
для неопредельного интеграла: 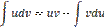 Для определенного:
Для определенного: 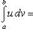
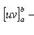
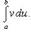 Предполагается, что нахождения интеграла
Предполагается, что нахождения интеграла 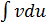 проще, чем
проще, чем 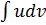 . В противном случае применение метода неопределенно.
. В противном случае применение метода неопределенно.
63. Несобственные интегралы. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода) При введении понятия определённого интеграла 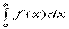 предполагалось, что выполняются следующие два условия: а) пределы интегрирования а и b являются конечными; б) подынтегральная функцияf(x) ограничена на отрезке
предполагалось, что выполняются следующие два условия: а) пределы интегрирования а и b являются конечными; б) подынтегральная функцияf(x) ограничена на отрезке 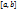 .Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным. Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования. Определение. Пусть функция определена и непрерывна на промежутке [a,+∞), тогда
.Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным. Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования. Определение. Пусть функция определена и непрерывна на промежутке [a,+∞), тогда
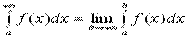 (12)называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода). Если
(12)называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода). Если 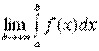 существует и конечен, то несобственный интеграл
существует и конечен, то несобственный интеграл 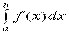 называется сходящимся; если данный предел не существует или равен ±∞ , то несобственный интеграл называется расходящимся. 64. Несобственные интегралы. Интеграл от разрывной функции (несобственный интеграл II рода)Определенный интеграл называется несобственным , если выполняются, по крайней мере , одно из следующих условий.1)Область интегрирования является бесконечной. Например, является бесконечным промежутком2)Функция является неограниченной в окрестности некоторых точек оюласти интегрирования Если на рассматриваемом отрезке [a,b] терпит разрыв второго рода , то мы имеем дело с несобственностью ll рода Рассмотрим функцию f(х) непрерывную на промежутке[a,b] . В точке b функция f(х) стремится к бесконечности.
называется сходящимся; если данный предел не существует или равен ±∞ , то несобственный интеграл называется расходящимся. 64. Несобственные интегралы. Интеграл от разрывной функции (несобственный интеграл II рода)Определенный интеграл называется несобственным , если выполняются, по крайней мере , одно из следующих условий.1)Область интегрирования является бесконечной. Например, является бесконечным промежутком2)Функция является неограниченной в окрестности некоторых точек оюласти интегрирования Если на рассматриваемом отрезке [a,b] терпит разрыв второго рода , то мы имеем дело с несобственностью ll рода Рассмотрим функцию f(х) непрерывную на промежутке[a,b] . В точке b функция f(х) стремится к бесконечности.
 | |||
 | |||




 а b
а b
 |
На отрезке[a,b,ε] функция f(x) будет непрерывна следовательно у нее существует определенный интеграл. Значение этого интеграла будет зависеть от ε . Несобственным интегралов ll рода называется предел этого определенного интеграла 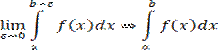 Если этот предел существует и конечен, то несобственный интеграл называется сходящимся , в противном случай расходящимс
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся , в противном случай расходящимс
65. Приложения определенного интеграла. Вычисление площадей плоских фигур Из геометрического смысла определенного интеграла следует, что площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), снизу отрезком[a,b] оси Ox, справа и слева прямыми x=a и x=b , находится по формуле 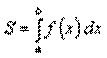 .
.
Если криволинейная трапеция расположена ниже оси Ox , то есть f(x)<0 , то площадь может быть найдена по формуле 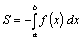 . Площадь фигуры, ограниченной кривыми y=f1(x) и y=f2(x) (f1(x)≤f2(x) для любого x
. Площадь фигуры, ограниченной кривыми y=f1(x) и y=f2(x) (f1(x)≤f2(x) для любого x 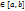 ), прямыми x=a и x=b , можно найти по формуле
), прямыми x=a и x=b , можно найти по формуле 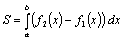 . Если криволинейная трапеция ограничена справа непрерывной кривойx=ϕ(y) , слева отрезком [c;d] оси Oy, снизу и сверху прямыми y=c и y=d , то ее площадь находится по формуле
. Если криволинейная трапеция ограничена справа непрерывной кривойx=ϕ(y) , слева отрезком [c;d] оси Oy, снизу и сверху прямыми y=c и y=d , то ее площадь находится по формуле 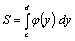 .
.
Если криволинейная трапеция ограничена кривой, заданной параметрическими уравнениями
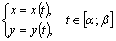 , то ее площадь находится по формуле
, то ее площадь находится по формуле 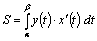 .
.
66. Приложения определенного интеграла. Вычисление длины дуги плоской кривой. Вычисление длины дуги плоской кривой Если функция y = f(x) непрерывна вместе с её производной f'(x) на отрезке [a, b], то длина дуги AB, где A(a,f(a)), B(b, f(b)), выражается формулой 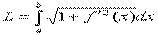 . Если кривая задана параметрическими уравнениями
. Если кривая задана параметрическими уравнениями 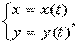
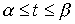 , где x(t), y(t) - дифференцируемые функции, то длина дуги
, где x(t), y(t) - дифференцируемые функции, то длина дуги 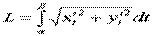 . Если дуга задана в полярных координатах
. Если дуга задана в полярных координатах 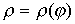 ,
, 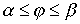 , то длина дуги
, то длина дуги 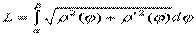 . Пусть кривая Г задана на плоскости OXY уравнением y=y(x),
. Пусть кривая Г задана на плоскости OXY уравнением y=y(x), 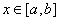 и
и 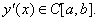 Тогда длинна этой кривой может быть вычислена по формуле:
Тогда длинна этой кривой может быть вычислена по формуле: 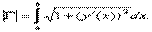
67. Приложения определенного интеграла. Вычисление объема телаВ общем случае, простого определенного интеграла не достаточно, чтобы вычислить объем тела, и для этого используются кратные интегралы. Лишь в некоторых частных случаях для вычисления объема используется простой интеграл. Самый простой случай – вычисление объема при известной площади сечения. Пусть дано какое-то объемное тело. Если площадь сечения задается функцией S(x), тогда объем этого тела, заключенный между плоскостями x = a и x = b вычисляется с помощью интеграла: 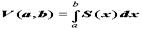 Частным случаем вычисления объема при известной площади сечения является вычисление объема тела вращения. Если некоторая кривая f(x) вращается вокруг оси x, тогда площадь сечения плоскостью x = u данного тела вращения равна площади круга с радиусом f(u), т.е. равна p f 2(u). В результате объем тела вращения, получаемого при вращении f(x) вокруг оси x, и ограниченного плоскостямиx = a и x = b равен :
Частным случаем вычисления объема при известной площади сечения является вычисление объема тела вращения. Если некоторая кривая f(x) вращается вокруг оси x, тогда площадь сечения плоскостью x = u данного тела вращения равна площади круга с радиусом f(u), т.е. равна p f 2(u). В результате объем тела вращения, получаемого при вращении f(x) вокруг оси x, и ограниченного плоскостямиx = a и x = b равен : 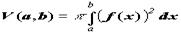
68. Функции нескольких (двух) переменных. Основные понятияПеременная z (с областью изменения Z) называется функцией двух независимых переменных x, y в множестве M, если каждой паре (x, y) из множества М по некоторому правилу или знаку ставится в соответствие одно определенное значение z из Z. Множество М, в котором заданы переменные x, y, называется область определения функции, а сами x, y- ее аргументами. Обозначения: 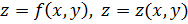 . Переменная z(c областью изменениячзависимых переменных ескольких незнкции, а сами тавится в соотвествие Z) называется функцией нескольких независимых переменных
. Переменная z(c областью изменениячзависимых переменных ескольких незнкции, а сами тавится в соотвествие Z) называется функцией нескольких независимых переменных 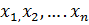 в множестве М, если каждому набору чисел
в множестве М, если каждому набору чисел 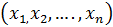 из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятие аргументов и области определения вводятся так же, как для функции двух переменных . Обозначения
из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятие аргументов и области определения вводятся так же, как для функции двух переменных . Обозначения