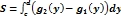Метод интегрирования по частям.

Пусть u=u(x) и v=v(x) – дифференцируемые функции. Тогда справедлива следующая формула интегрирования по частям:

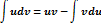
С помощью этой формулы вычисление интеграла 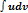сводится к отысканию другого интеграла .

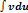Применение формулы целесообразно в тех случаях, когда интеграл 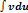более прост для нахождения, чем исходный либо подобен ему.

При этом в качестве uследует брать такую функцию, которая при дифференцировании упрощается, а в качестве dv – ту часть подынтегрального выражения интеграл от которого известен или может быть найден. Иногда формулу интегрирования по частям приходится применять несколько раз.

Основные типы простейших рациональных дробей.

А/х-а

2) А/(х-а)^к, (k³ 2, kÎN)

3) А/х²+рх+q, (D=p²-4q<0)

4)Ax+B/x²+px+q, (D=p²-4q<0)

5)Ax+B/(x²+px+q)^k, (k³ 2, kÎN, D=p²-4q<0)

где A, a, B, p, qÎR.

Интегрирование рациональных дробей с помощью разложения их на простейшие дроби.

Перед интегрированием рациональной дроби 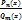, необходимо выполнить следующие алгебраические преобразования и вычисления.

1. Если дана неправильная рациональная дробь, выделить из неё целую часть, разделив числитель на знаменатель столбиком, т.е. представить эту дробь в виде:

,

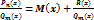где M(x) – многочлен, 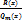–правильная рациональная дробь.

2. Разложить знаменатель дроби на линейные и квадратичные множители:

,

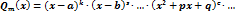где D=p²-4q<0.

3.Правильную рациональную дробь разложить на простейшие дроби:

,

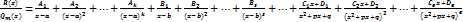где A_i, B_i, C_i, D_i, … - неизвестные пока что коэффициенты.

4.Вычислить неизвестные коэффициенты A_i, B_i, C_i, D_i, … к общему знаменателю, прировнять в числителе коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов.

Можно определить коэффициенты и другим способом придавая в полученном тождестве переменной х поочерёдно столько произвольных числовых значений, сколько неизвестных коэффициентов и решить систему.

Интегрирование иррациональных функций.

Интегралы вида

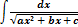
с помощью выделения полного квадрата

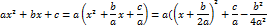
и последующей замены

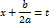
приводится к одному из интегралов:

1)

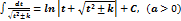
или

2)

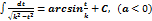
Интегрирование тригонометрических выражений с помощью универсальной тригонометрической подстановки.

1)Интеграл вида: 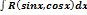приводит к интегрированию от рациональной функции с помощью универсальной тригонометрической подстановки: 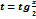.В результате получим: 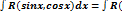2t/1+t², 1-t²/1+t²)*2dt/1+t²

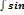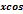2)Интеграл вида: ^{m n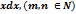} находят:

а) при нечётной n: t=sinx

б) при нечётной m: t=cosx

в) если m и n чётные: sinx*cosx=1/2sin2x sin²x=1/2(1-cos2x) cos²x=1/2(1+cos2x)

Свойства определённого интеграла.

1)

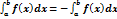
2)

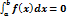
3)

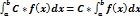
4)

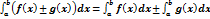
5)

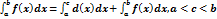
6)если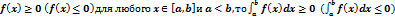

7) если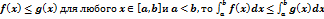

8) если f(x)интегрируема на отрезке [a,b] и для этого отрезка имеет место неравенство m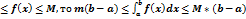

Методы вычисления определённого интеграла.

1)Формула Ньютона-Лейбница: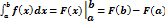

2) Замена переменной: а)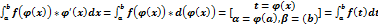

б)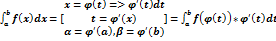

3)Интеграл по частям: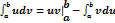

Применение определённого интеграла к вычислению площадей плоских фигур.

1)

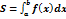
2)

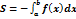
3)

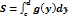
4)

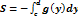
5)

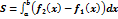
6)