Наибольшее и наименьшее значения функции на отрезке.

Наибольшим значением функции y=f(x) на промежутке X называют такое значение 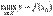, что для любого 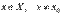справедливо неравенство .

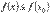Наименьшим значением функции y=f(x) на промежутке X называют такое значение 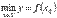, что для любого 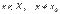справедливо неравенство .

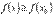Рассмотрим правило нахождения наибольшего и наименьшего значений функции на отрезке :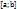

1)найти критические точки функции на интервале ;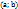

2)вычислить значения функции в найденных критических точках;

3)вычислить значения функции на концах отрезка, т.е. в точках ;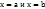

4)среди всех вычисленных значений функции выбрать наибольшее и наименьшее.

Замечания : 1. Если функция 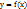на отрезке 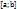имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение. 2. Если функция 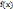на отрезке не имеет критических точек, то это означает, что на нем функция монотонно возрастает или убывает.

Выпуклость графика функции. Связь с производной II-го порядка.

График дифференцируемой функции 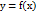называется выпуклым вниз на интервале (a;b), если он расположен выше любой ее касательной на этом интервале. График функции называется выпуклым вверх на интервале (a;b), если он расположен ниже любой ее касательной на этом интервале.

Интервалы выпуклости вниз и вверх находят с помощью следующей теоремы.

Теорема: Если функция 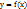во всех точках интервала (a;b) имеет отрицательную вторую производную, т.е. 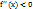, то график функции в этом интервале выпуклый вверх. Если же 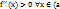;b) – график выпуклый вниз.

Точки перегиба. Необходимое условие существования точки перегиба.

Точка, в которой функция определена и в которой функция меняет направление выпуклости, называется точкой перегиба.

В окрестности такой точки X0 график функции y = f (x) слева и справа от точки X0 имеет разные направления выпуклости.

Необходимое условие существования точки перегиба:

Теорема. Пусть функция y = f (x) дважды непрерывно дифференцируема на интервале (a, b). Для того, чтобы точка М(x0, f(x0)) была точкой перегиба графика функции y = f (x) необходимо, чтобы f " (x0) = 0.

Необходимые условия наличия перегиба:

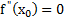либо 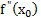не существует.

Достаточное условие существования точки перегиба.

Теорема. Пусть функция y = f (x) имеет вторую производную f "(x) в некоторой достаточно малой окрестности точки x0 интервала (a, b), за исключением, быть может самой точки х0, а график функции имеет касательную в точке С = (х0, f (x0)). Если при переходе через точку х0 вторая производная f "(x) меняет знак, то точка С является точкой перегиба графика функции y = f (x).

Достаточные условия наличия перегиба:

1. Если 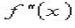меняет знак при переходе через точку x0, то x0 - точка перегиба.

2. Если при n четном x0 -

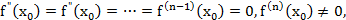
точка перегиба, при n нечетном x0 не является точкой перегиба.

Асимптоты графика функции.

Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различают вертикальные, наклонные и горизонтальные асимптоты.

Вертикальной асимптотой графика функции y=f(x) называется вертикальная прямая 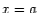, если lim (x→a) f(x)=∞ или lim (x→a+0) f(x)=∞, или lim (x→a-0) f(x)=∞.

Наклонной асимптотой графика функции y=f(x) при x→+∞ называется прямая y=kx+b, если выполнены два условия: 1) некоторый луч (a; +∞) целиком содержится в D(f); 2) расстояние по вертикали между графиком и прямой стремится к 0 при x→+∞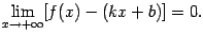

Наклонной асимптотой графика функции y=f(x) при x→ - ∞ называется прямая y=kx+b, если выполнены два условия: 1) некоторый луч (-∞; a) целиком содержится в D(f); 2) расстояние по вертикали между графиком и прямой стремится к 0 при x→ - ∞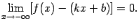

В случае, если наклонная асимптота расположена горизонтально, то есть при k=0, она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая y=c=const является горизонтальной асимптотой графика y=f(x) при x→+∞ или x→-∞, ес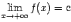ли или 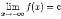соответственно.
45. Общая схема исследования функции и построения графика.

Исследование функции у = f (х) целесообразно вести в определенной последовательности.

1. Найти область определения функции.

2. Найти (если это можно) точки пересечения графика с осями координат.

3. Найти интервалы знакопостоянства функции (промежутки, на Которых f(х) > 0 или f(х) < 0).

4. Выяснить, является ли функция четной, нечетной или общего Ища.

5. Найти асимптоты графика функции.

6. Найти интервалы монотонности функции.

7. Найти экстремумы функции.

8. Найти интервалы выпуклости и точки перегиба графика функ­ции.

9. На основании проведенного исследования построить график функ­ции. Заметим, что приведенная схема исследования не является обя­зательной.
46. Понятие неопределенного интеграла.

Неопределенным интегралом от функции f(x) называется совокупность всех ее первообразных.

Если функция F(x) является первообразной ф-ии f(x) на (a,b), то множество всех первооб-х для f(x) задается формулой F(x)+C, где С-постоянное число.

Множество всех первооб-х ф-ий F(x)+C для f(x) наз-ся неопределенным интегралом от ф-ии f(x) и обозначается символом ∫f(x)dx. Таким образом, по определению ∫f(x)dx=F(x)+C.

Операция нахождения неопределенного интеграла от ф-ии наз. интегрированием этой ф-ии.