Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.

Если закон распределения неизвестен, то есть основания предположить, что он имеет определенный вид (назовем его А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А.

Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределения, т.е. при помощи специально подобранной случайной величины – критерия согласия.

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Имеется несколько критериев согласия: «хи квадрат» К. Пирсона, Колмогорова, Смирнова и др. Ограничимся описанием применения критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется и для других распределений, в этом состоит его достоинство). С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.

Обычно эмпирические и теоретические частоты различаются.

Случайно ли расхождение частот? Возможно, что расхождение случайно (незначимо) и объясняется либо математическим числом наблюдений, либо способами их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.

Критерий Пирсона отвечает на поставленный выше вопрос. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений.

Итак, пусть по выборке объема n получено эмпирическое распределение.

Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты n_i^’. При уровне значимости α требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.

В качестве критерия проверки нулевой гипотезы примем случайную величину

(*)

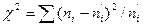Эта величина случайная, т.к. в различных опытах она принимает различные, заранее неизвестные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия (*), и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.

Доказано, что при 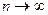закон распределения случайной величины (*) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения «хи квадрат» с k степенями свободы.

Проверить гипотезу о нормальном распределении можно последующему алгоритму:

1. Вычислить теоретические частоты

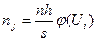
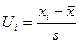
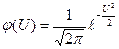
2. Сравнить эмпирические и теоретические частоты с помощью «хи квадрат» распределения.

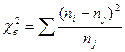
3. χ²_кр находится по таблице критических точек χ²-распределения по уровню значимости α и числу степеней свободы k=m-3, где m – число групп.

4. Если 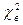< χ²_кр , то гипотезу о нормальном распределении принимают.

Метод наименьших квадратов.

Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости f:

x	x1	x2	…	xn
f(x)	y1	y2		yn

Нужно найти формулу, выражающую эту зависимость аналитически. Поставим задачу таким образом, чтобы обязательно учитывать характер исходной функции: найти функцию заданного вида: y=F(x), которая в точках x₁, .., x_n принимает значения как можно более близкие к табличным значениям y₁, …, y_n.

Практически вид приближающей функции F можно определить следующим образом. По таблице строится точечный график функции f, а затем проводится плавная кривая, по возможности наилучшим образом отражающая характер точек.

Строгая функциональная зависимость для экспериментально полученной таблицы наблюдается редко, т.к. каждая из участвующих в ней величин может зависеть от многих случайных факторов. Однако формула y=F(x) (ее называют эмпирической формулой) позволяет находит значения функции f для не табличных значений х, «сглаживая» результаты измерений величины y.

Рассмотрим один из таких способов, называемый метод наименьших квадратов.

Предположим, что приближающая функция F в точках x₁, .., x_n имеет значения 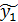, …, 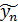(1). Будем рассматривать совокупность значений функции f из таблице и совокупность (1) как координаты двух точек n-мерного пространства. Задача приближения функции F ставится следующим образом: найти такую функцию F заданного вида, чтобы расстояние между точками М(y₁, …, y_n) и 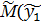, …, 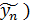была наименьшей. Используя формулу расстояния между двумя точками получаем, что величина 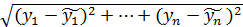была наименьшей, что равносильно, что функция Q= 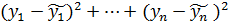→min.

В качестве приближающих функций в зависимости от точечного графика функции f часто используют следующие функции:

1) y=ax+b 2) y=ax²+bx+c 3) y=ax^m 4) y=ae^mx 5) y= 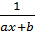6) y=alnx+b

7) y=a/x+b 8) y=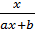

Когда вид приближающей функции установлен, задача сводится только к отысканию значений параметров.

Рассмотрим метод отыскания параметров приближающей функции на примере линейной функции: y=ax+b, 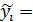ax_i+b. Задача сводится к исследованию на минимум функции .

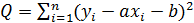Используем необходимо условие минимума: , .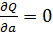

,

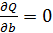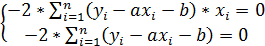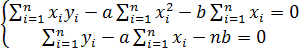
Делим каждое уравнение на n

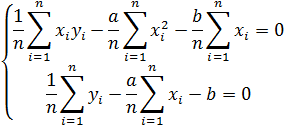
Введем обозначения:

, , , = .

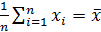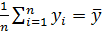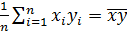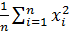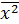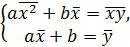
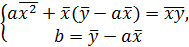
a= 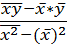b= .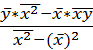

Значения найденной функции будут отличатся от табличных значений. Разности 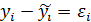называются отклонениями измеренных значений y от вычисленных .

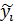После преобразований функций 3-8 можно для нахождения оценки параметров использовать найденные формулы для параметров линейной функции.

3) y=ax^m, lny=lna+mlnx. Введем новые переменные u=lnx, v=lny. находим оценки линейной функции v=Au+B, где m=A, a=e^B. Таким образом, строим новую таблицу, прологарифмировав х и y, по новой таблице найти параметры А и В и затем параметры а и m.

4) y=ae^mx, lny=lna+mx. Логарифмируем y, х остается без изменения. m=A, lna=B.

5) y= 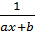, , 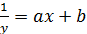в таблице x остается без изменения, y заменяется на 1/y.

6) y=alnx+b - логарифмируем х.

7) y=a/x+b - заменяем х на 1/х.

8) y= 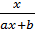, 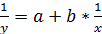- заменяем х на 1/х, y заменяется на 1/y.

Корреляционный анализ.

Корреляционный и регрессионный анализ являются смежными разделами математической статистики и предназначены для изучения зависимость одного показателя от другого. Связи между различными явлениями в природе сложны и многообразны. В технике чаще всего речь идет о функциональной зависимости. В большинстве случаев интересующие нас явления протекают в условиях воздействия на них множества неконтролируемых факторов. Воздействие каждого из этих факторов в целом невелико, при этом связь теряет строгую функциональность и система переходит не в строго определенное состояние, а в одно из множества возможных. Речь идет о стохастической связи.

Под стохастической мы понимаем такую связь, когда одна случайная переменная реагирует на изменения другой случайной переменной изменением своего закона распределения.

Исследование взаимосвязи величин приводит к теории корреляции как разделу теории вероятностей и корреляционному анализу как разделу математической статистики. Исследование зависимости случайной величины от ряда неслучайных и случайных величин приводит к моделям регрессии и регрессионному анализу на базе выборочных данных.

Парная корреляция

Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.

Корреляционная зависимость двух случайных величин задается моделью X=X(Y,Z), Y=Y(X,Z) - Z -набор внешних случайных факторов.

Парная корреляция занимается изучением характеристик взаимосвязи двух случайных величин. Основой получения этих характеристик служит совместное распределение

F(x,y)=P{X<x, Y<y}.

Из теории вероятностей нам известно, что коэффициент корреляции 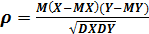служит для анализа зависимости двух случайных величин.

Если случайные величины X и Y независимы, то ρ=0.

Наиболее естественной оценкой коэффициента корреляции является выборочный коэффициент корреляции

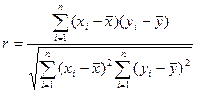
Распределение статистики r зависит только от объема выборки и коэффициента корреляции ρ и не зависит от остальных параметров случайного вектора (X, Y), а сама статистика r является состоятельной асимптотически эффективной оценкой коэффициента корреляции ρ.

Если r=0, то выборки независимы.

Проверка гипотезы о значимости выборочного коэффициента корреляции.

Далее проверяют гипотезу о значимости коэффициента корреляции:

Н₀: ρ=0 при Н₁: ρ≠0.

Для этого вычисляется выборочное значение:

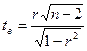
t_кр находится по таблице критических точек распределения Стьюдента по уровню значимости α и числу степеней свободы k=n-2. Если 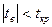, то принимают гипотезу H₀, т.е. зависимость не существует.

Коэффициент корреляции принимает значения 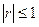.Принято считать, что если |r|<0,3 - то связь слабая; при 0,3<|r|<0,7 - средняя; при |r|≥0,7 - сильная или тесная (линейная). Когда |r|=1 - функциональная.

Регрессионный анализ.

Парная регрессия

При изучении статистических связей, форму связей характеризует функция регрессии. В случае парной регрессии имеется только детерминирующий фактор x и регрессионная модель записывается следующим образом: y= 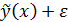, где 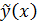- детерминирующая составляющая, 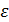- случайная составляющая с независимыми значениями, M 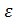=0.

Оценка параметров регрессии в условиях конкретной ситуации проводится по статистической совокупности, которая рассматривается в качестве выборки (x_i, y_i).

Если |r|→1, то используется линейная регрессия 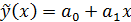и для нахождения параметров метод наименьших квадратов.

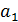- это коэффициент регрессии характеризует влияние, которое оказывает изменения Х на Y. Он показывает на сколько единиц в среднем изменится Y при изменении Х на одну единицу.

С учетом полученных формул для коэффициентов линейной регрессии методом наименьших квадратов и формулы для выборочного коэффициента корреляции, уравнение линейной регрессии может быть записано в виде:

.

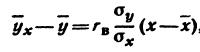Представление связи через линейную функцию там, где на самом деле существуют нелинейные соотношения, вызывает упрощенные или ложные положения и выводы на основе аналитического уравнения. Вопрос о нелинейности формы уравнения следует решать на стадии теоретического анализа. Для этого используется корреляционное поле и можно выбрать зависимости представленные в методе наименьших квадратов.

Проверка значимости параметров выборочного уравнения регрессии.

В качестве меры того, насколько хорошо регрессия описывает данную систему наблюдений, служит коэффициент детерминации, при этом за базу сравнения принято описание с помощью среднего арифметического. Составляются следующие суммы отклонений:

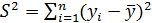- фактических значений от среднего арифметического

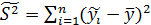-выравненных значений от среднего арифметического

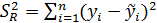-фактических от выравненных.

.

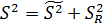Коэффициент детерминации .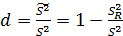

Таким образом, чем «ближе» этот коэффициент к единице, тем лучше описание.

Вывод о правильности выбора вида взаимосвязи и характеристику значимости всего уравнения регрессии получают с помощью F-критерия, вычисляя его выборочное значение по формуле: .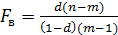

m - число параметров в уравнении регрессии.

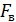должно быть больше 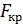при к₁=m-1 и к₂=n-m степенях свободы.

В противном случае следует пересмотреть форму уравнения, перечень переменных и т.д.